表示学习

状态和表示

马尔科夫链

我们假设，动态系统在时间t时候的状态为x~t~
动态系统的重要假设——具有马尔可夫性质：未来的状态仅依赖于当前的状态，而与过去的状态无关。
换句话说，状态x~t+1~在给定当前状态x~t~的条件下，与过去的状态x~t-1~，x~t-2~…是条件独立的，数学表示为：
P(x~t+1~∣x~t~,x~t−1~,…,x~1~)=P(x~t+1~∣x~t~)

补充：条件概率：P(A|B) = P(AB) / P(B)

我们将这样的系统建模为马尔科夫链

状态估计

马尔科夫链假设系统的状态是完全可观测的，即状态是已知的。但在实际中，系统在时间 t 的状态通常是未知的，因为我们无法直接观测到状态。我们的任务是从带噪声的传感器观测值中估计真实状态，这一过程称为状态估计。此类系统是部分可观测的，可以通过**隐藏马尔科夫模型（HMM）**来建模，因为状态是“隐藏”的。我们假设状态 x~t~ 仍然遵循马尔科夫过程，同时假设时间 t 的观测值 z~t~ 仅依赖于该时刻的状态 x~t~，而与所有之前的状态和观测值无关：
P(z~t~|x~t~,x~t-1~,…,x~1~)=P(z~t~|x~t~)

这意味着观测模型 h(⋅) 只依赖于 x~t~ 来预测当前的观测值 z~t~，即 h(x~t~) = z~t~ 用一个视觉的例子来具体说明。如果我们是一辆自动驾驶汽车，其摄像头捕获了下图所示的场景，我们需要知道所有交通参与者的状态，以避免碰撞。这些状态包括每个对象的 3D 位置、边界框大小，可能还包括速度。然而，这些信息并不是直接提供给我们的，而是必须通过传感器的观测数据（例如立体图像、RGB 图像或激光雷达数据）来估计。

考虑动作或者输入

在未来关于最优估计的课程中，我们将考虑机器人动作或控制输入对这些马尔科夫过程的影响，进一步探讨状态是如何演变的。具体来说，动态方程将从简单形式 f(x~t~）= x~t+1~ 扩展到 f(x~t~,u~t~) = x~t+1~ 其中 u~t~ 是机器人在 t 时间所采取的控制输入或者动作
例如对于汽车，控制输入可能是方向盘的转向角度或油门的输出值。一个有趣的问题是如何决定下一个最佳动作 u~t~。这被称为决策问题。

马尔科夫链可以推广到马尔科夫决策过程（Markov Decision Processes, MDPs），而隐藏马尔科夫模型则可以推广到部分可观测马尔科夫决策过程（Partially Observable Markov Decision Processes, POMDPs），用于正式描述决策问题。如果对这一主题感兴趣，可以考虑学习斯坦福大学的《Decision-Making under Uncertainty》（不确定性下的决策）课程，其链接为 https://web.stanford.edu/class/aa228/cgi-bin/wp/。

生成式和判别方法

如何从观测值中估计状态？让我们以从输入的 RGB 图像（观测值 z）中估计物体的姿态（状态 x）为例，探讨这一问题。6D 姿态通常指物体的 3D 平移和 3D 旋转，共 6 个参数。
我们可以从高层次概述两种方法，具体细节将在课程的后续部分深入探讨。

贝叶斯公式补充

生成式模型

生成式模型描述了观测值 z 和状态 x 的联合概率分布 p(z,x) 。根据贝叶斯公式，该分布可以通过观测值的似然 p(z∣x) 和状态的先验分布 p(x) 计算得到。

以下是一个关于物体姿态估计的具体示例：

采样：
我们可以从 p(x) 中采样一个物体的姿态 x^(i)^。先验分布 p(x) 可以是简单的均匀分布（假设物体可能出现在空间中的任何位置），也可以更复杂，例如反映物体可能出现在特定区域（如汽车在道路上，而不是建筑物旁边）。

生成观测值：
对于采样到的姿态 x^(i)^，使用观测模型 h(x^(i)^) 生成最可能的观测值 z^(i)^。例如，可以将物体在采样姿态下的 2D 投影投射到图像平面上。

计算似然：
通过比较实际观测值 z 和生成的观测值 z^(i)^，得到似然值 p(z|x^(i)^)，即假设姿态 x^(i)^ 下观测值为 z 的概率(衡量实际值 z 和假设观测值 z^(i)^ 的匹配程度)。

最后综合所有可能的 x^(i)^ 对应的 p(z|x^(i)^) 生成一个完整的 p(z|x)，进而计算出联合分布 p(z, x)

判别式模型

判别式模型描述的是状态 x 给定观测值 z 时的条件概率 p(x∣z) 。例如，我们可以训练一个神经网络（如下图5所示的 PoseCNN），直接将输入的图像 z 映射为最可能的姿态输出 x

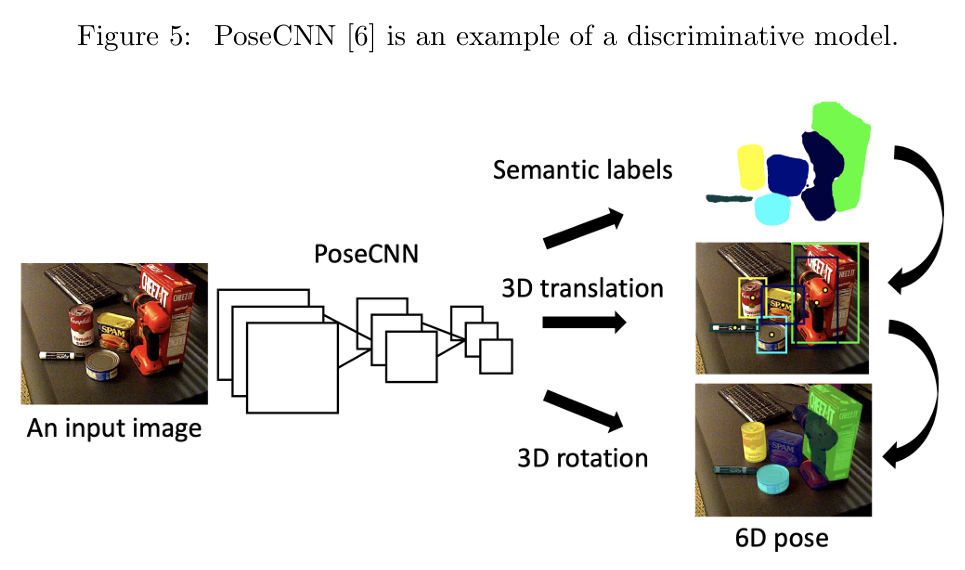
生成式和判别式的进一步差别请见CS229的notes：https: //cs229.stanford.edu/notes-spring2019/cs229-notes2.pdf

计算机视觉中的表示

我们将注意力转向表示这个术语在计算机视觉领域的使用。在高层次的语义分割流水线中（如下图6所示），数据在流水线中的任何阶段都具有特定的表示。因此，为了更清晰地定义表示的含义，我们需要结合上下文。

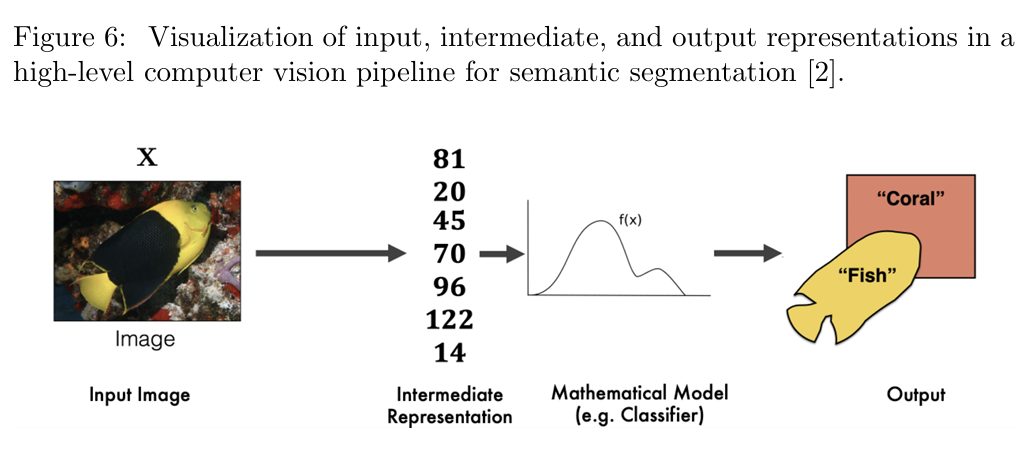
输入表示

在流水线的一端，我们有通过传感器捕获的原始数据。输入表示描述了原始传感器数据的格式。例如，在图 6 中，输入是一幅包含鱼的 3D 场景的观测图像。根据传感器的选择，原始数据可能以 2D 图像、深度图像或点云的形式表示。即使是在特定形式内，输入表示也存在细微差别。例如：

彩色图像与灰度图像；
双目视觉与单目视觉；
RGB 颜色空间与 HSV 颜色空间。

输出表示

在流水线的另一端，从原始传感器数据推断出的信息以输出表示的形式呈现。这种表示简洁地描述了场景的高层关键特征，这些特征对决策任务至关重要。例如：

如果目标是统计遇到的鱼的数量，相关的输出表示可能是“鱼”标签，甚至是更具体的鱼的种类。
如果目标是无人机在珊瑚礁中导航，则可能更感兴趣于鱼的 6D 姿态和 3D 边界框信息，这些信息有助于路径规划。

中间表示

在输入表示和输出表示之间，数据通常会以某种中间表示形式存在。中间表示通常是一种压缩的低维向量，用于总结高维的输入传感器数据。输入表示提供的数据通过中间表示被压缩和处理，而中间表示进一步用于推导输出表示中的相关特征。

表示好坏的标准

自然问题：什么是“好”的表示？
表示对决策至关重要。那么，什么样的表示才算是“好”的表示？Bengio 等人提出了以下标准：

紧凑性（Compact）
表示应该是最小的，即在尺寸上尽量紧凑。
表达性（Explanatory）
表示应足够具有表达力，能够捕获大量可能的输入配置。
可解耦性（Disentangled）
输入数据变化的不同解释因素应该独立表示，这反映了这些因素可以独立变化。
分层性（Hierarchical）
表示应该具有分层结构，使得更抽象的概念可以通过更低级别的概念进行解释。这有助于特征的复用并提高计算效率。
下游任务友好性
表示应该使后续的推断、预测或决策问题变得更简单。因此，表示的质量可以通过下游任务的性能来衡量。

传统计算机视觉与可解释表示

传统计算机视觉流水线

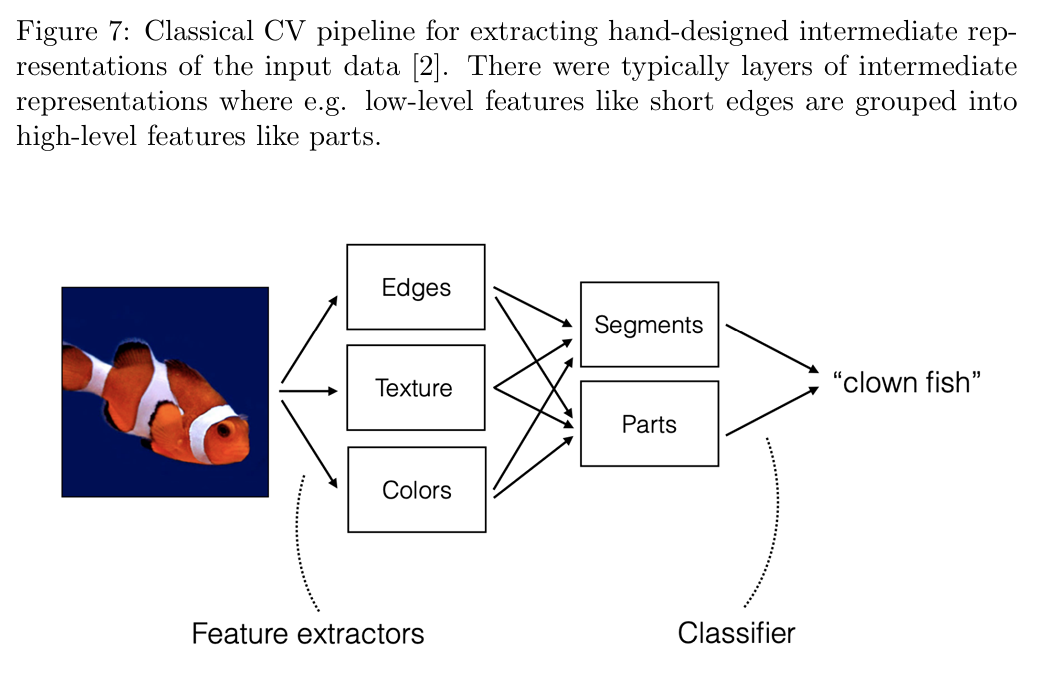
传统（2012 年之前）的计算机视觉流水线在高层次上如上图7所示。输入数据被压缩成中间表示，这些中间表示通常由从输入中提取的手工设计特征组成。特征的选择具有灵活性，可以根据任务具体化。例如：

如果认为鱼身上的条纹可以用来区分不同的鱼类，可以通过提取边缘和颜色来构成中间表示。

图 7 所示的例子中，输出表示是一个类别标签。为了推断该类别标签，中间表示被输入一个分类器，该分类器可以是学习得到的，也可以是基于手工定义的启发式方法。例如，我们可以定义一个简单的启发式规则：“如果图像颜色直方图中包含大量橙色和白色，则该图像可能包含小丑鱼”。

传统方法的优缺点

优点：可解释性
由于这些方法是手工设计的，因此我们可以轻松解释为什么选择特定的输出表示。例如，在医学或法律等高风险领域中，这种解释能力尤为重要。
缺点：开发耗时
设计特征提取器是一个繁琐的过程，往往需要大量的时间和领域知识。而且，当知识不足时，设计质量可能下降。

现代计算机视觉与学习的表示

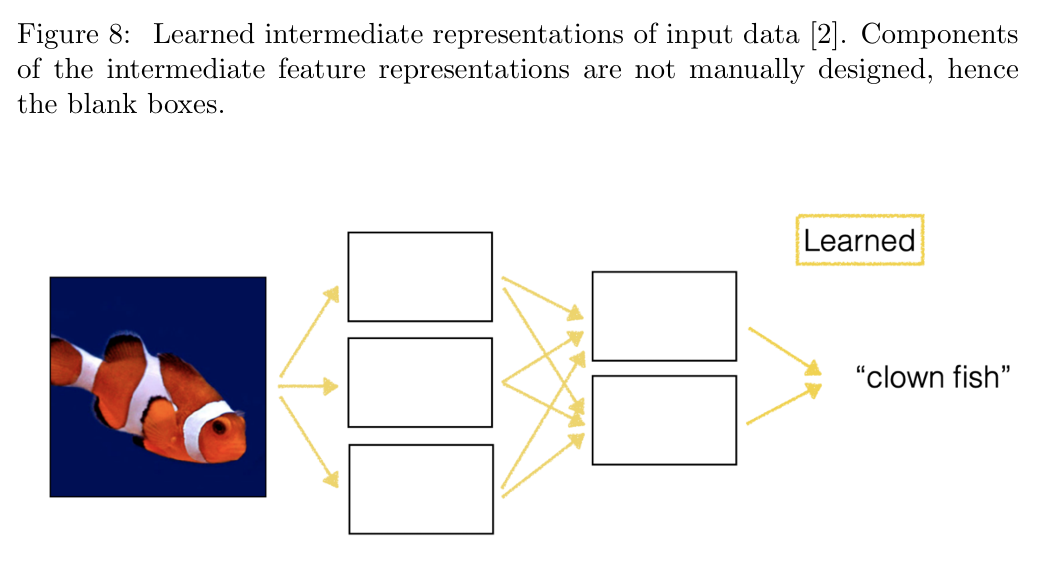
现代计算机视觉方法（大约从 2012 年开始）通过学习的中间表示取代了手工提取的特征。这些方法的高层次可视化如图 8 所示。

卷积神经网络（CNN）

目前最常见的模型架构之一是卷积神经网络（Convolutional Neural Networks, CNN）。这些网络通过对输入图像应用卷积滤波器的多层处理，逐层提取特征。这些卷积滤波器的参数通常通过带标签的训练数据学习而来，从而自动生成输入数据的中间表示。与传统的手工设计特征相比，学习得到的表示在为后续分类器提供关键信息方面表现得更加强大。

学习表示的优势与挑战

优势：更高的准确性
学习表示在下游任务（如图像分类）中表现出更高的准确性。这是因为它能够从数据中自动提取复杂特征，而不需要人工干预。
挑战：缺乏可解释性
虽然学习表示提高了性能，但它们往往缺乏可解释性。相比传统方法，学习得到的表示更难解释其高性能的来源，以及如何改进模型。

可视化学习表示的方法

为了解释学习表示的性能，研究人员提出了一些方法：

激活图分析
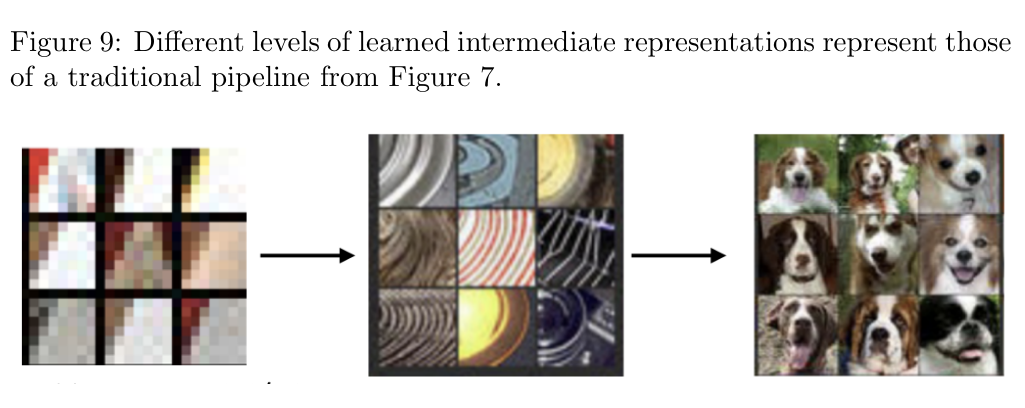
Zeiler 和 Fergus 的研究分析了卷积神经网络中每层卷积滤波器对图像中哪些区域的响应最强。例如，他们发现 CNN 中学习到的表示（图 9）类似于传统流水线中提取的特征（如边缘、纹理、身体部位等，见图 7）。
降维可视化
另一种理解学习表示的方法是将其投射到低维空间中，以便于绘制和解释。常用的技术之一是 t-SNE（t-分布随机邻域嵌入），它通过最小化高维表示与低维嵌入之间的 KL 散度，将高维数据投射到低维空间。这样可以直观显示来自同一类别的数据点在低维空间中的聚集情况（如图 10 所示）。

无监督学习和自监督学习

传统监督学习的局限性

在传统的监督学习框架中，模型针对特定的推断任务进行训练，以最小化在训练数据集上的损失函数（例如图像分类准确性或姿态估计误差）。训练数据由 D 个样本组成，形式为 (x~i~,y~i~)，其中：

x~i~：输入数据（如图像或 3D 点云）；
y~i~：输出标签（如物体类别或 6D 姿态）。

尽管数据通常很丰富，但标签的获取代价昂贵，且可能需要领域专家的专业知识。

无监督学习：自编码器

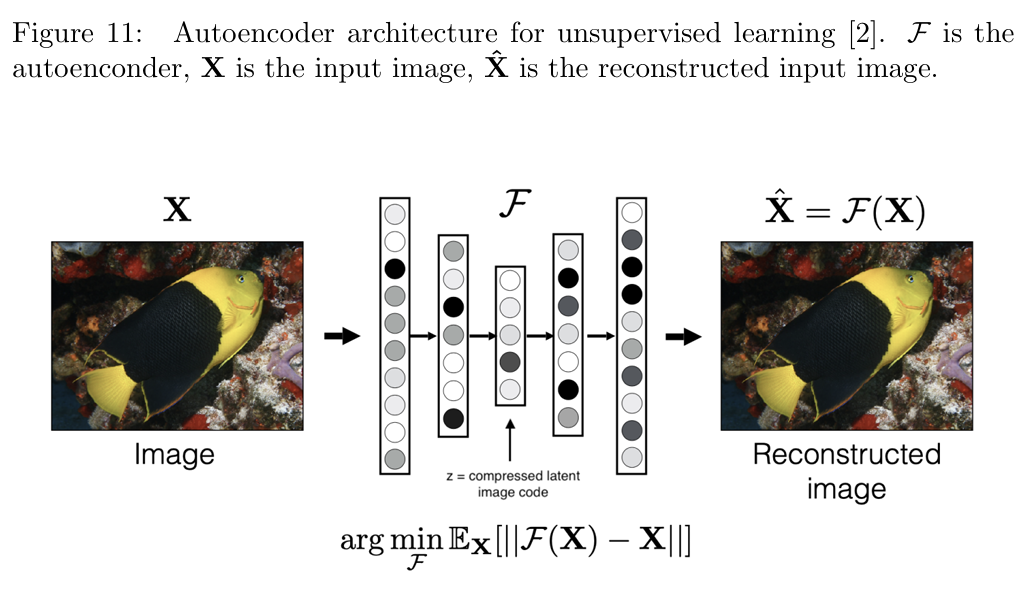
无监督学习的目标是从无标签数据中学习有意义的表示。例如，自编码器（autoencoder）的架构如图 11 所示，其目标是完美重建输入图像。自编码器的关键组成部分是中间表示（称为“瓶颈”），位于网络的中间层：

输入与重建：自编码器的输入为 X ，输出为重建后的数据 $\widehat{X}$ 。模型通过最小化重建误差（即 X 和 $\widehat{X}$ 之间的差异）来学习。
瓶颈的作用：瓶颈表示是一种压缩的低维表示，能够在更高效的表示中保留输入数据的重要信息。

具体说明：

输入数据 X：
模型接收一张图片 X 作为输入，比如一个普通的图像。
编码器部分（Encoder）：
自编码器的前半部分称为编码器。它会将输入图片 X 压缩成一个低维的中间表示 z，也叫瓶颈（Bottleneck）。这个 z 是对图片的重要特征的压缩版本，比如它可能保留图片中的轮廓或结构信息。
解码器部分（Decoder）：
自编码器的后半部分称为解码器。它试图从 z 中还原出与原图 X 尽量相似的图片 $\widehat{X}$ 。输出图片 $\widehat{X}$ 是自编码器对输入的“记忆”。
训练目标：
自编码器的目标是让输出图片 $\widehat{X}$ 尽可能接近原始图片 X。模型通过比较 X 和 $\widehat{X}$ 的差异（称为重建误差）来调整参数，逐步学习到输入图片的核心特征。

为什么无监督？

在整个过程中，自编码器只需要原始图片 X，不需要额外的标签（如图片中物体的名称）。它通过学习如何“重建”图片来提取特征，这就是无监督学习的特点。

例子：压缩和重建 想象你有一张复杂的图片，比如一条五颜六色的鱼。自编码器的编码器部分可能会压缩这条鱼的图像，把颜色信息（比如橙色和白色的条纹）和轮廓信息提取出来，然后解码器用这些信息重建图片。这相当于抓住了图片的核心要素，而忽略了细枝末节。

自监督学习

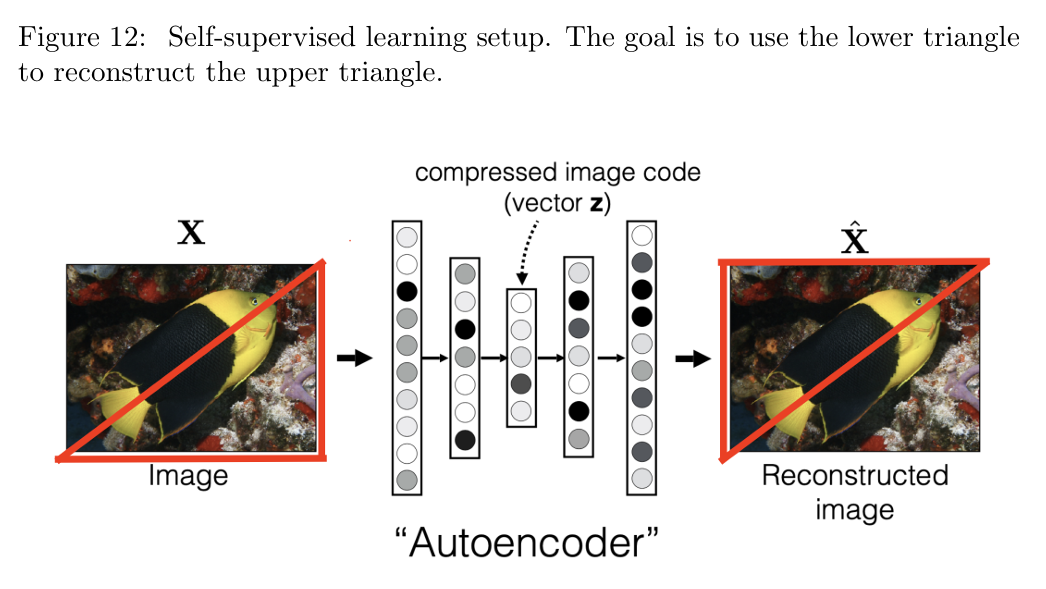
自监督学习通过遮挡部分输入数据来创造伪标签，从而模拟监督学习的过程。它是无监督学习的一种特殊形式。它通过对数据进行“人为操作”来生成伪标签，从而将无标签数据转化为有标签数据，模拟监督学习的过程。例如，图 12 展示了一个自监督学习的任务：保留图像对角线以下的像素作为输入，并以对角线以上的像素作为输出标签。通过这样的任务，模型可以学习输入图像的有意义表示。

输入数据处理：
给定一张完整的图片，先人为遮挡部分数据，比如只保留图片的下半部分作为输入。
目标伪标签：
被遮挡的部分（上半部分）被当作模型的“输出标签”。模型的任务是根据输入的下半部分，预测被遮挡的上半部分。
训练过程：
模型会尝试根据图片下半部分的特征，预测出上半部分的内容。例如，模型可以学习到图片中连续的颜色、形状和纹理等信息，从而完成任务。

为什么是自监督？

原始图片中的“遮挡部分”并不是外部标注的，而是由我们人为操作生成的。这就是“自监督”的核心思想：从原始数据中创造伪标签。
模型通过这种“填空式”的训练方式，学习到了图片内部的特征关系，比如颜色的连续性或物体的形状。

例子：鱼的图片 假设我们有一张鱼的图片，图像的上半部分有鱼头和身体，下半部分是鱼尾。模型输入鱼尾的部分，任务是预测鱼头的部分。通过训练，模型可能会学习到：

鱼尾的颜色条纹和鱼头的颜色条纹之间的关系。
鱼头和鱼尾在形状上的连续性。

总结：无监督与自监督的优势

通过自编码器或自监督学习，可以在大量无标签数据上学习到有意义的中间表示。随后，这些表示可以用于下游任务（例如分类），并且只需少量标签数据即可实现良好的性能。

单目深度估计和特征跟踪

本章节将讨论表示学习在计算机视觉中的两个常见问题的应用：单目深度估计和特征跟踪

单目深度估计

深度估计可以看作是对应问题（Correspondence Problem）的一个特殊案例，这是计算机视觉中的基础问题。对应问题的核心是找到 3D 场景中某个物理点在多个 2D 图像中的投影点的位置。2D 图像可以通过单目相机或立体相机从不同视角捕获。

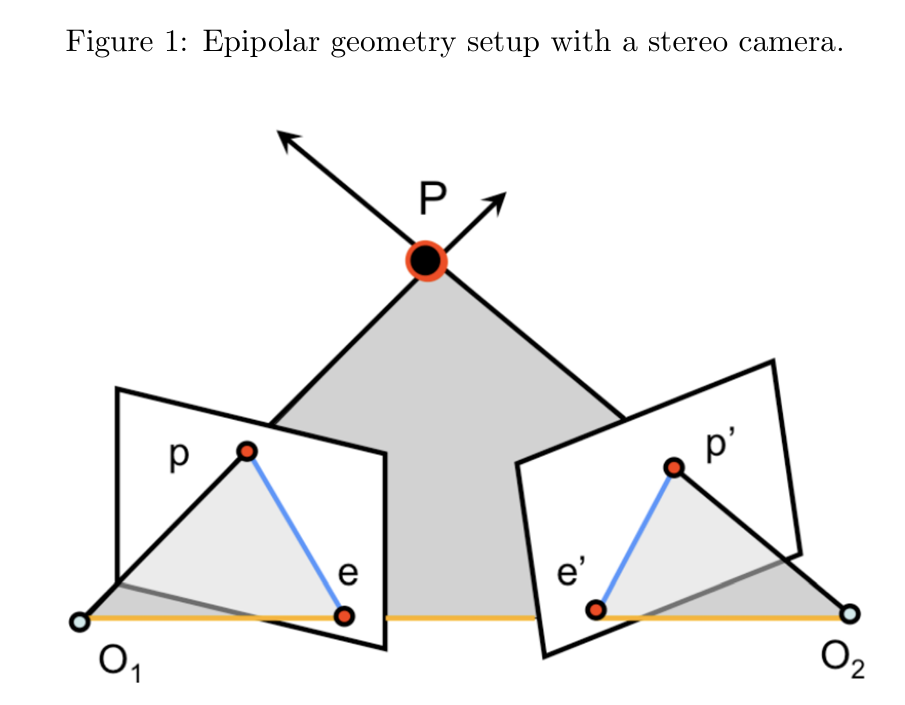
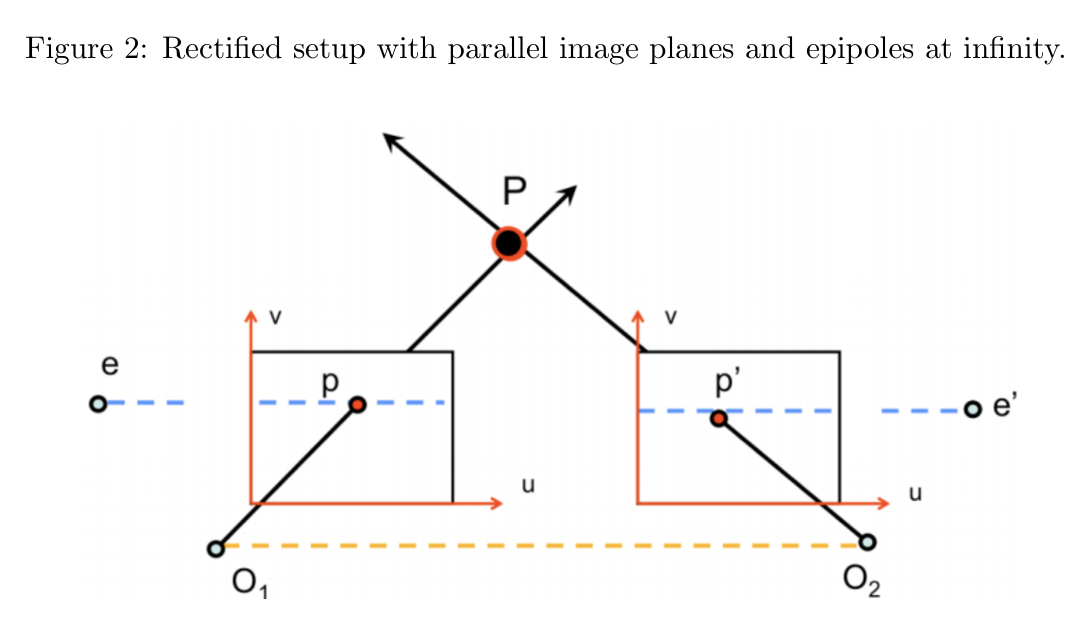
一种解决对应问题的方法是利用极线几何（Epipolar Geometry），如图 1 所示。这部分内容在课程前面已经介绍过。回顾一下，给定相机的两个中心点 O~1~ 和 O~2~，以及场景中的一个 3D 点 P，其在左右相机图像中的投影点分别为 p 和 p′。根据极线约束（Epipolar Constraint），已知左图像中的点 p 后，可以确定右图像中对应的点 p′ 必定位于右相机的某条极线上。

极线是通过图像平面与极平面（Epipolar Plane）的交线确定的。这一约束由两个相机之间的基本矩阵（Fundamental Matrix）或本质矩阵（Essential Matrix）表示，因为基本矩阵能够给出已知的极线。在深度估计的背景下，我们通常假设使用的是一个立体相机系统，并且图像经过了校正。此时，极线是水平的，视差（Disparity）被定义为两个对应点之间的水平距离，即：

d = p~u~′ − p~u~，因此有：p~u~ + d = p~u~’
注意，对于所有点 P 来说，都会满足 p~u~′ > p~u~

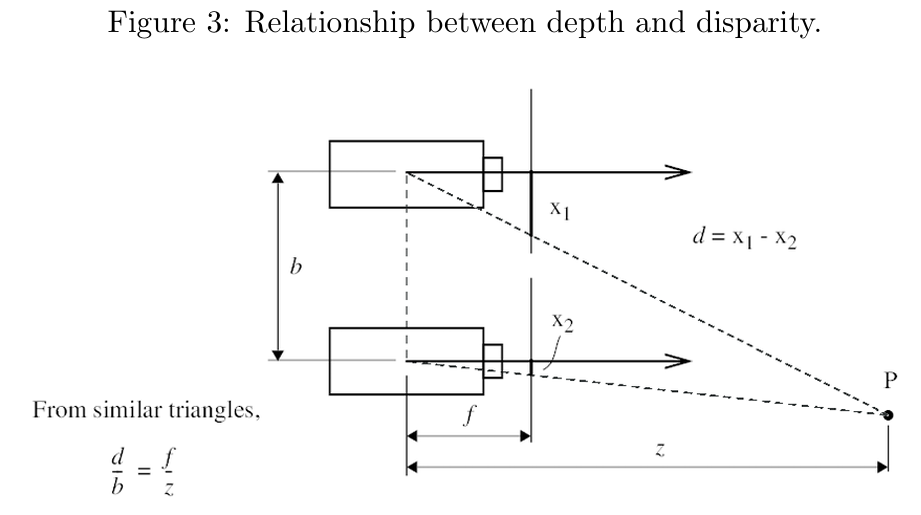
视差和深度之间存在一个简单的反比关系，其中深度被定义为点 P 相对于相机中心的 z 坐标。我们可以通过图 3 中所示的相似三角形关系得到以下公式：

z = f * b / d

其中，f 是相机的焦距，b 是两个相机之间的基线长度（如图 2 中黄色虚线所示）。

假设基线 b 和相机的内参矩阵 K 是已知的，那么如果我们能够在两张校正后的图像中找到对应关系（如图 2 所示），我们就能够计算视差 d，进而推导出深度。

一种确定 p′ 对应于 p 的方法是沿另一张图像中的极线进行简单的 1D 搜索，利用像素或局部图像块的相似性来确定最可能的 p′ 位置。然而，这种简单的方法会在真实世界的图像中遇到诸多问题，例如：
遮挡（Occlusions）：有些像素可能无法在另一张图像中找到对应点；
重复模式（Repetitive Patterns）：重复的图案会导致混淆；
均匀区域（Homogeneous Regions）：纹理缺乏的区域难以匹配。
为了解决这些问题，我们转而采用现代的表示学习方法。

监督深度估计

这里我们关注单目（单视角）深度估计的任务：在测试时，仅使用单张图像，并且对场景内容不做任何假设。相比之下，立体（多视角）深度估计方法需要多张图像作为输入进行推断。

单目深度估计是一个欠约束问题（Underconstrained Problem），也就是说，从几何上无法仅凭一张图像确定每个像素的深度。然而，人类仅凭一只眼睛就可以很好地估计深度，这是因为人类可以利用以下线索：
透视（Perspective）：远处物体看起来更小；
比例（Scaling）：物体在场景中的尺寸关系；
外观（Appearance）：通过光照和遮挡信息推断物体相对位置。
通过利用这些线索，计算机也可以仅凭单张图像推断深度。

监督方法的实现

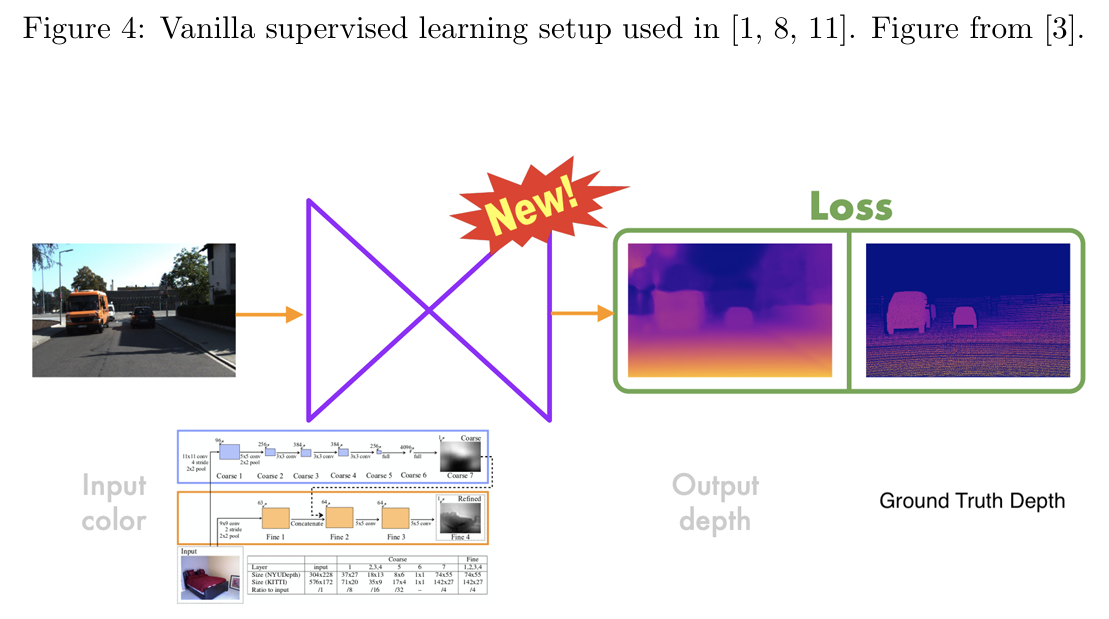
完全监督学习方法（如图 4 所示）依赖于训练模型（通常是卷积神经网络，CNN），以预测每个像素的视差值。训练使用的是包含真实深度（Ground Truth Depth）和 RGB 图像对的数据集。训练过程中，损失函数用于度量预测的深度与真实深度之间的相似性，模型通过最小化损失函数来学习。

由于单目方法只能估计深度的比例关系（Depth Up-to-Scale），一些研究（如 [1]）提出了使用比例不变误差（Scale-Invariant Error）来改进单目深度估计的方法。

无监督深度估计

尽管监督学习方法在深度估计任务中取得了不错的效果，但它们的应用受限于场景类型，因为这些方法需要大量的真实深度数据。而真实深度数据的获取往往代价高昂。这种局限性促使研究者提出了无监督学习方法。这类方法只需要输入的 RGB 图像数据和一个具有已知内参的立体相机，从而避免了高昂的标注成本。

在无监督深度估计中，我们以 [3] 提出的方法为例。其核心思想是利用图像重建作为目标任务，而不是直接使用真实深度数据。基本实现方式如下：

输入数据：网络输入左视图 I^l^；
输出视差：CNN 网络输出视差值 d^l^，该视差值表示将右视图 I^r^ 中的像素平移到左视图的距离；
图像重建：通过视差值 d^l^，将右视图中的像素采样重建为左视图的版本 $$\tilde{I}^{l}$$；
损失计算：损失函数衡量原始左视图 I^l^ 和重建图像 $$\tilde{I}^{l}$$ 之间的差异。

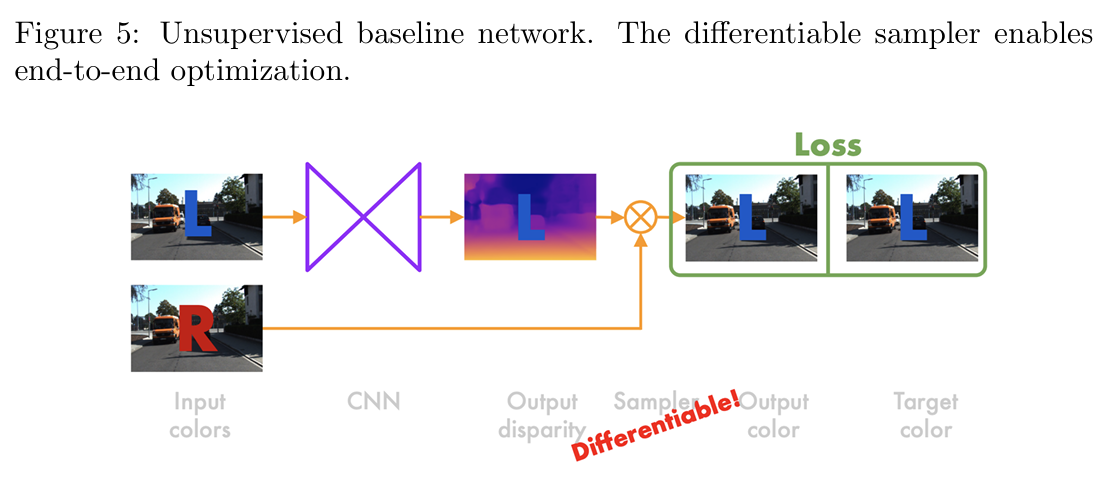
如图 5 所示，基础网络架构由一个卷积神经网络（CNN）组成，其输入为左视图图像 $I^l$ 。网络会生成对应的视差图 $d^l$ 。接着，利用双线性采样器从右视图 $I^r$ 中采样像素来构造重建的左视图 $\tilde{I}^l$ 。采样公式如下：

$\tilde{I}^l(u, v) = I^r(u - d^l(u, v), v)$

由于视差值 $d^l(u, v)$ 通常不是整数，因此像素的确切位置可能不存在。为了实现端到端的优化，训练过程中使用了一个完全可微的双线性采样器，使得网络可以进行梯度更新。尽管训练时同时使用左右视图，但在测试时只需要左视图就可以推断出左对齐的深度信息。网络架构是全卷积的，包括一个编码器和一个解码器，输出多种分辨率的视差图。例如：
第一张视差图的分辨率为 $(D_h, D_w)$ ；
第二张视差图的分辨率为 $(2D_h, 2D_w)$ 。

改进的无监督网络

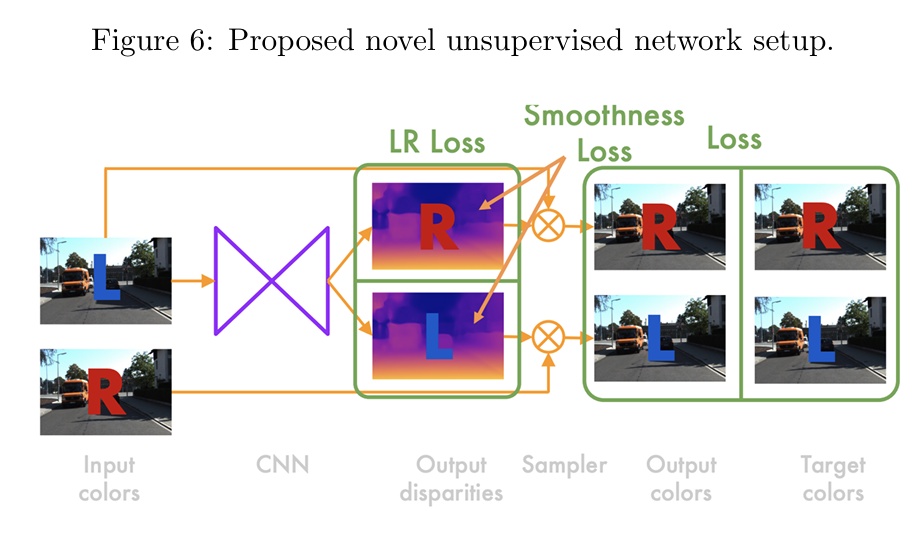
在[3]基础网络上，研究者提出了一种新的架构，能够同时重建左视图和右视图（如图 6 所示）。这一改进允许引入更加复杂的损失函数，从而提升视差图的质量。

改进后的网络接收输入的左视图 $I^l$ ，计算出：
左对齐的视差图 $\tilde{d}^l_{i,j}$ ；
右对齐的视差图 $\tilde{d}^r_{i,j}$ 。
右对齐视差图包含了将左视图转换为右视图所需的水平位移。同样地，左对齐视差图用于将右视图转换为左视图。

通过前述的采样器，可以从视差图生成：
重建的左视图 $\tilde{I}^l$ ；
重建的右视图 $\tilde{I}^r$ 。
损失函数计算输入的左右视图和重建视图（共四幅图像）之间的差异。

损失函数

总损失函数 $C$ 是所有尺度损失之和： $$ C = \sum_s C_s $$ 其中，每个尺度的损失 $C_s$ 由以下三部分组成：

重建损失（Reconstruction Loss） 衡量重建图像与原始图像之间的相似性，公式为： $$ C^l_{ap} = \frac{1}{N} \sum_{i,j} \left( \alpha \frac{1 - \text{SSIM}(I^l_{ij}, \tilde{I}^l_{ij})}{2} + (1-\alpha) |I^l_{ij} - \tilde{I}^l_{ij}| \right) $$ 其中， $\text{SSIM}$ 是结构相似性指数， $\alpha = 0.85$ ，表示对 SSIM 的权重更高。
平滑损失（Smoothness Loss） 惩罚视差图中的梯度变化，公式为： $$ C^l_{ds} = \frac{1}{N} \sum_{i,j} \left( |\partial_x d^l_{ij}| e^{-|\partial_x I^l_{ij}|} + |\partial_y d^l_{ij}| e^{-|\partial_y I^l_{ij}|} \right) $$ 这项损失鼓励视差图的平滑性，但在原始图像的边缘区域放宽约束，以保留清晰的物体边界。
左右一致性损失（Left-Right Consistency Loss） 确保左右视差图的一致性，公式为： $$ C^l_{lr} = \frac{1}{N} \sum_{i,j} |d^l_{ij} - d^r_{ij + d^l_{ij}}| $$

这一无监督设置在结果中表现优于基线方法和现有的完全监督方法。

自监督深度估计

在单目深度估计的背景下，模型在测试阶段只使用单张图像。尽管通过监督方法（例如使用真实深度标注数据）可以很好地训练出模型，但这种方法在实际应用中受限于标注数据的高成本。因此，自监督方法应运而生，它能够利用未标注的单目视频数据进行训练，而无需真实深度数据。

核心思想

自监督深度估计的核心是利用视频帧之间的几何关系和图像重建来指导深度学习。以下是基本的工作流程：

相机运动的几何约束：通过估计连续视频帧之间的相对相机位姿（camera pose），利用视差图和相机运动推导出场景的深度信息。
图像重建：网络预测深度图，然后根据几何约束将某一帧图像的像素重投影到另一帧图像中，从而实现重建。

训练阶段

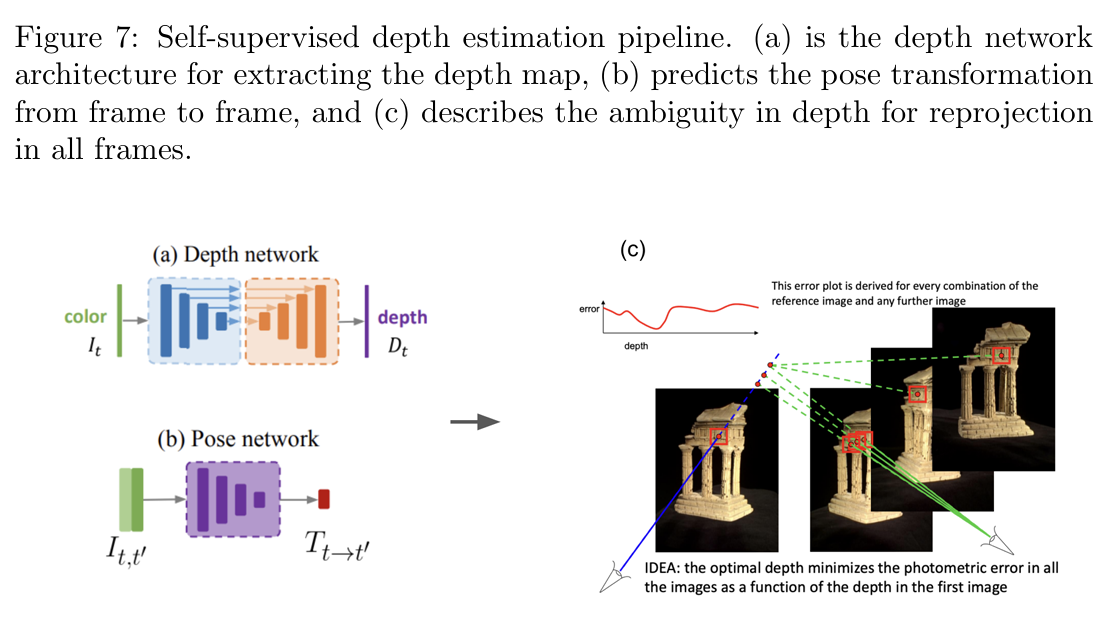
在训练阶段，自监督方法通常需要以下三部分网络：

深度网络（Depth Network）
输入：单帧图像输出：深度图 $D_t$ ，即每个像素点的深度值。

位姿网络（Pose Network）
输入：相邻的两帧图像输出：相机位姿变化 $[R, t]$ ，即从一帧到另一帧的旋转和位移。

图像采样器（Image Sampler）
功能：通过深度图 $D_t$ 和位姿 $[R, t]$ ，将当前帧图像的像素点重投影到目标帧图像中，从而生成重建图像。

公式化过程

对于图像中某一点 $(u, v)$ ，其在相机坐标系中的深度为 $z$ ，可以通过深度图 $D_t$ 得到： $$ P_t = K^{-1}[u, v, 1]^T D_t(u, v) $$
其中：
$P_t$ ：该点在当前帧相机坐标系下的三维坐标；
$K$ ：相机的内参矩阵。通过相机位姿变换 $[R, t]$ ，该点可以映射到下一帧图像的相机坐标系中： $$ P_{t+1} = R P_t + t $$ 然后将该点投影回图像平面，得到在目标帧图像中的像素坐标 $(u', v')$ ： $$ [u’, v’]^T = K P_{t+1} $$

损失函数

自监督方法的损失函数类似于无监督方法，但稍有不同。以下是自监督方法常用的损失函数：
重建损失（Reconstruction Loss） 衡量重建图像 $\tilde{I}_t$ 和原始图像 $I_t$ 的相似性： $$ L_{photo} = \sum_{u,v} |I_t(u,v) - \tilde{I}_t(u,v)| $$ 或使用更复杂的度量方法（如 SSIM）。

平滑损失（Smoothness Loss） 和无监督深度估计类似，平滑损失用于确保深度图的平滑性，同时保留图像边缘。

遮挡处理（Occlusion Handling） 视频中可能存在遮挡现象，即某些点在当前帧中可见，但在目标帧中不可见。遮挡处理通过掩码机制忽略这些点，避免误差传播。

测试阶段

在测试阶段，模型只需要单帧图像作为输入即可预测深度图。位姿网络在测试时通常不需要使用，因为相机运动信息主要用于训练阶段。

优势与局限性

优势：
无需真实深度标注数据，适合应用于大规模数据集。
通过视频数据进行训练，能够捕捉场景中的动态信息。
局限性：
对相机运动的假设要求较高。如果相机运动估计不准确，会影响深度预测。
遮挡处理和动态物体的处理仍是一个挑战。

特征跟踪

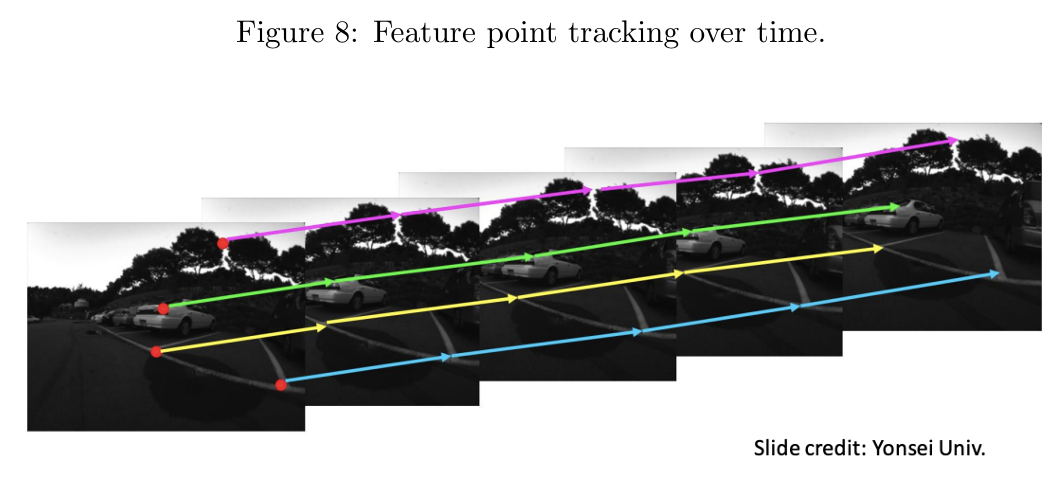
动机（Motivation）

给定一系列图像，特征跟踪任务旨在追踪一组二维点在所有图像中的位置，如图 8 所示。与深度估计类似，特征跟踪可以被视为解决图像序列中对应问题的另一种实例。

特征跟踪

特征跟踪可以用于追踪场景中物体的运动轨迹。我们对场景的内容或相机的运动方式不作任何假设：相机可能在移动或静止，而场景可能包含多个动态或静止的物体。

特征跟踪的难点在于确定哪些特征点可以高效地跨帧跟踪。特征的外观可能因为以下原因而在连续帧中发生显著变化：

相机运动：特征可能完全从视野中消失；
阴影变化：光照变化导致特征难以识别；
遮挡：某些特征点被其他物体遮挡。

此外，随着特征跟踪模型的外观信息更新，细微的误差可能逐渐累积，导致“漂移”（drift）。我们的目标是找到在跟踪中容易识别且稳定的区域（称为特征或关键点），然后应用简单的跟踪方法来持续找到这些对应点。

传统方法

传统上，图像中容易跟踪的显著特征通常通过手工设计的方法检测和跟踪。这些方法（如 Harris Corner 和 SIFT 特征）会为显著特征生成特定的描述符，用于快速匹配其他图像中的相似点。这些描述符编码了特征点的纹理、梯度等信息，便于后续匹配。然而，这些方法通常是稀疏的，即仅为图像中的部分像素生成描述符。

表示学习的应用

在这一部分，我们探讨如何使用表示学习来学习图像特征的描述符，而不是依赖手工设计。

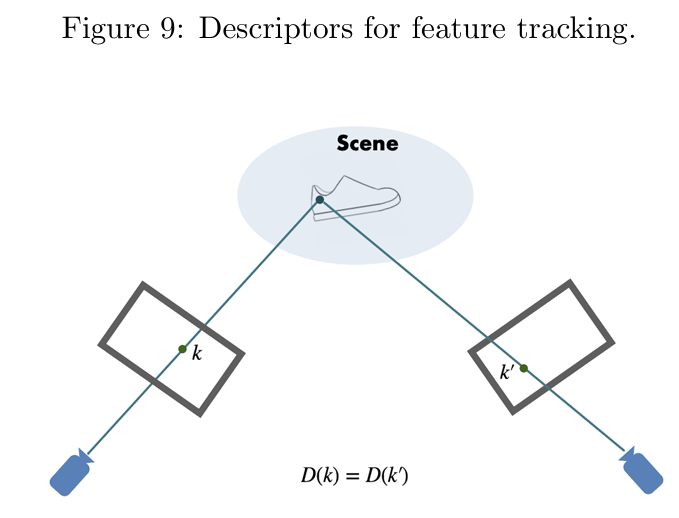
如图 9 所示， $D(k)$ 表示像素 $k$ 的特征描述符，通常是一个高维向量。假设 $k$ 和 $k'$ 是对应的点，且来源于同一个 3D 场景点。尽管它们出现在不同的图像中（可能视角、光照有所变化），我们仍希望它们的描述符相同，即 $D(k) = D(k')$ 。这样，我们可以通过描述符的相似性在图像间匹配像素，实现高效的特征跟踪。

学习密集描述符

我们研究了文献 [2] 中提出的一种学习密集描述符的方法。

方法概述

如图 10 所示，给定一个输入的彩色图像，我们希望学习一个映射 $f(\cdot)$ ，该映射为彩色图像中的每个像素输出一个 $D$ 维描述符。“密集”在此表示我们为输入图像中的每个点生成描述符，而不仅仅是稀疏的一组点。为了便于可视化，图 10 中将 $D$ 维描述符通过降维映射到 RGB。实际上， $f(\cdot)$ 是一个通过卷积编码器-解码器架构训练得到的神经网络。该网络通过像素对比损失训练，尝试通过最小化相似描述符之间的距离并最大化不同描述符之间的距离来反映像素的“对比”。

配对匹配损失

如图 11 所示，我们假设给定了一组图像配对（称为匹配）的对应关系。我们对图像中的所有点运行网络以计算描述符。对于每个真实匹配，我们计算两个对应点描述符之间的 L2 距离。我们的目标是最小化描述符空间中的距离 $D(I_a, u_a, I_b, u_b)^2$ 。
配对匹配损失公式为： $$ L_{\text{matches}}(I_a, I_b) = \frac{1}{N_{\text{matches}}} \sum_{N_{\text{matches}}} D(I_a, u_a, I_b, u_b)^2 $$

非匹配损失

对于非匹配点对（即不对应的点对），我们计算一个对比损失项。如图 12 所示，我们希望最大化非对应点之间的距离。公式如下： $$ L_{\text{non-matches}}(I_a, I_b) = \frac{1}{N_{\text{non-matches}}} \sum_{N_{\text{non-matches}}} \max(0, M - D(I_a, u_a, I_b, u_b)^2) $$
其中， $M$ 是最大距离，确保最大化的距离在一个固定范围内。

总损失

总损失是两部分的和： $$ L(I_a, I_b) = L_{\text{matches}}(I_a, I_b) + L_{\text{non-matches}}(I_a, I_b) $$

数据获取

为了大规模且低人工干预地获取真实的对应关系，作者提出使用机器人系统进行自动化和自监督的数据收集。如图 13 所示，利用机器人手臂在不同姿态下捕获静止物体的图像。由于机器人手臂的正向运动学是已知的，我们可以获得相机姿态和对应视图的配对。结合所有视图的 3D 重建，可生成所需的真实对应关系。

交叉对象损失

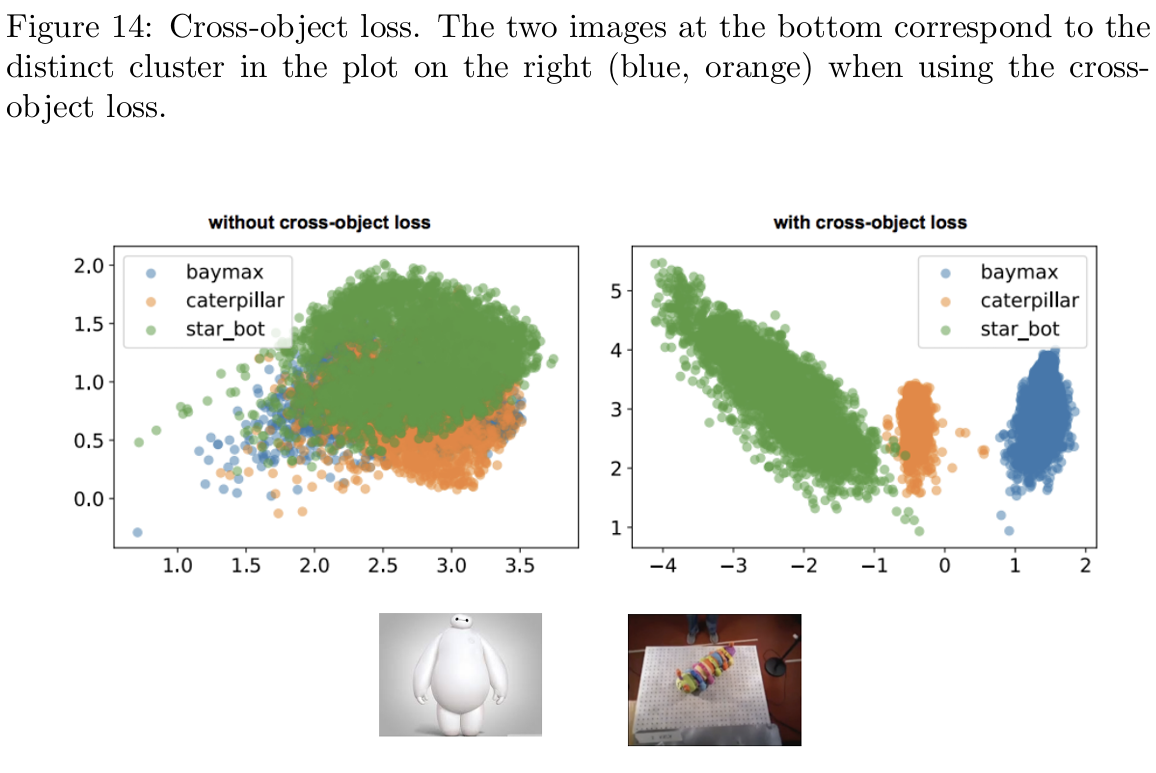
如图 14 所示，如果仅在相同对象的图像对上进行训练，不同对象的描述符可能会重叠，而这不符合期望。为此，引入了交叉对象损失（不同对象图像像素对都视为非匹配），训练后可以看到描述符空间中形成了清晰的聚类。

类一致性描述符

如图 15 所示，对于同一类的对象（如帽子），即使视觉外观不同，其描述符仍然具有相似的结构和颜色。

参考文献

David Eigen, Christian Puhrsch, and Rob Fergus.
Depth map prediction from a single image using a multi-scale deep network.
arXiv preprint arXiv:1406.2283, 2014.
（通过多尺度深度网络从单张图像预测深度图。）

Peter R Florence, Lucas Manuelli, and Russ Tedrake.
Dense object nets: Learning dense visual object descriptors by and for robotic manipulation.
arXiv preprint arXiv:1806.08756, 2018.
（密集对象网络：通过和为了机器人操作学习密集视觉对象描述符。）

Clément Godard, Oisin Mac Aodha, and Gabriel J Brostow.
Unsupervised monocular depth estimation with left-right consistency.
In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 270–279, 2017.
（具有左右一致性的无监督单目深度估计。）

Clément Godard, Oisin Mac Aodha, Michael Firman, and Gabriel J Brostow.
Digging into self-supervised monocular depth estimation.
In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 3828–3838, 2019.
（深入研究自监督单目深度估计。）

C. Harris and M. Stephens.
A combined corner and edge detector.
In Proceedings of the 4th Alvey Vision Conference, pages 147–151, 1988.
（一种结合角点和边缘的检测器。）

Max Jaderberg, Karen Simonyan, Andrew Zisserman, et al.
Spatial transformer networks.
Advances in Neural Information Processing Systems, 28:2017–2025, 2015.
（空间变换器网络。）

David G Lowe.
Distinctive image features from scale-invariant keypoints.
International Journal of Computer Vision, 60(2):91–110, 2004.
（基于尺度不变关键点的显著图像特征。）

Nikolaus Mayer, Eddy Ilg, Philip Hauser, Philipp Fischer, Daniel Cremers, Alexey Dosovitskiy, and Thomas Brox.
A large dataset to train convolutional networks for disparity, optical flow, and scene flow estimation.
In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 4040–4048, 2016.
（用于视差、光流和场景流估计的大规模数据集，用于训练卷积网络。）

K. Mikolajczyk and C. Schmid.
A performance evaluation of local descriptors.
IEEE Transactions on Pattern Analysis and Machine Intelligence, 27(10):1615–1630, 2005.
（局部描述符性能评估。）

Krystian Mikolajczyk and Cordelia Schmid.
Scale & affine invariant interest point detectors.
International Journal of Computer Vision, 60(1):63–86, 2004.
（尺度和仿射不变的兴趣点检测器。）

Ashutosh Saxena, Min Sun, and Andrew Y Ng.
Make3d: Learning 3d scene structure from a single still image.
IEEE Transactions on Pattern Analysis and Machine Intelligence, 31(5):824–840, 2008.
（Make3D：从单张静态图像学习三维场景结构。）

Jianbo Shi and Carlo Tomasi.
Good features to track.
In IEEE Conference on Computer Vision and Pattern Recognition, pages 593–600, 1994.
（适合追踪的优秀特征。）

光流和场景流

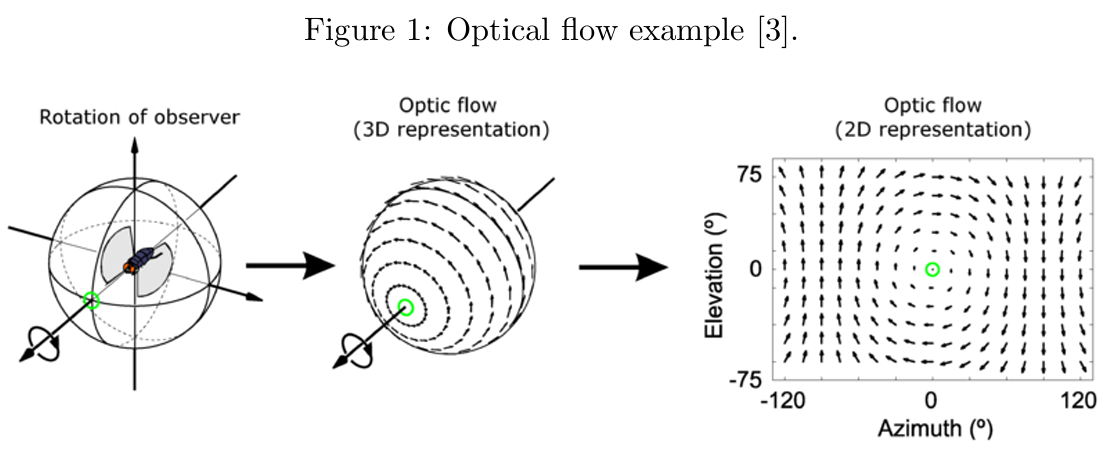
给定一个视频，光流被定义为一个二维向量场，它描述了由于相机（观察者）与场景（对象、表面、边缘）之间的相对运动，每个像素的表观移动情况。相机、场景或两者都可能处于运动状态。图1显示了一个旋转的飞虫从自身视角呈现的逆时针旋转方向。尽管场景是静态的，表观运动的二维光流却指示围绕原点的相反（顺时针）方向旋转。

光流与运动场

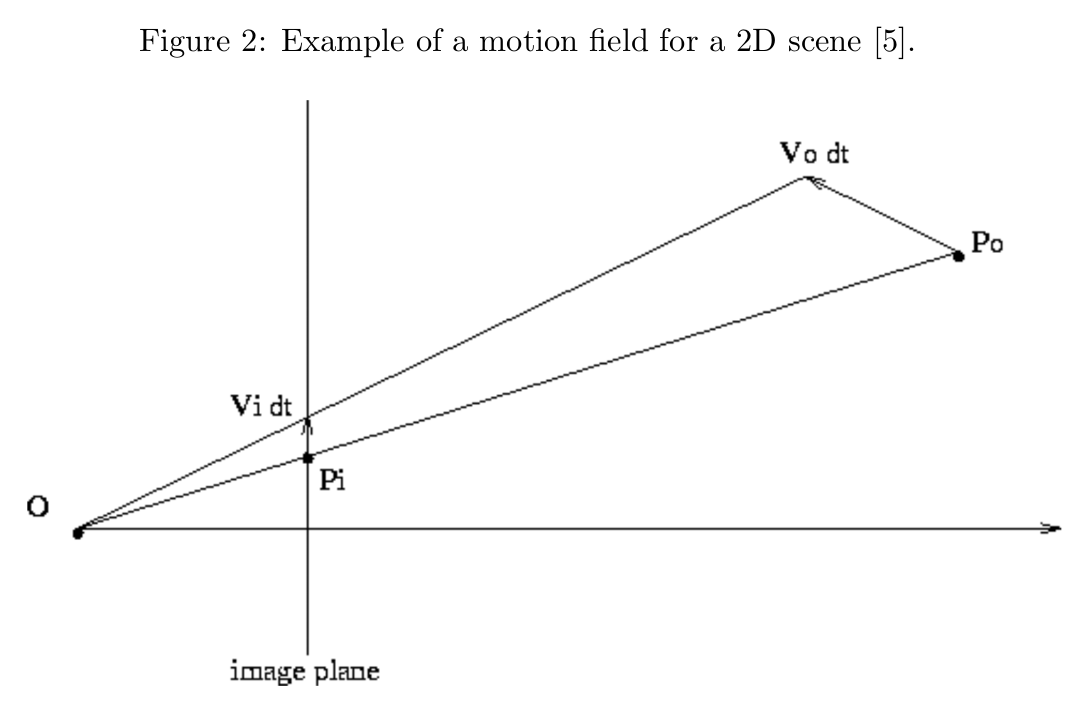
光流不应与运动场混淆，后者是一个二维向量场，描述了场景中点的三维运动矢量投影到观察者图像平面上的情况。图2展示了一个简单二维场景中的运动场（可以想象为从俯视角观察三维场景）。二维物体点 $P_o$ 被投影到图像平面上的一维点 $P_i$ ，由观察者 $O$ 所见。
如果物体点 $P_o$ 按照运动矢量 $V_o \cdot dt$ 发生位移，相应的投影一维点将以 $V_i \cdot dt$ 移动。此处的一维运动场包含了图像平面上所有位置 $i$ 的速度值 $V_i$ 。

推广到三维场景

对于像素 $(x, y)$ 的运动场，由以下公式给出： $$ \begin{bmatrix} u \ v \end{bmatrix} = \begin{bmatrix} \frac{dx}{dt} \ \frac{dy}{dt} \end{bmatrix} = M x’ $$ 其中， $x' = \begin{bmatrix} \frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt} \end{bmatrix}^T$ 表示三维点的运动，
$M \in \mathbb{R}^{2 \times 3}$ 包含了像素位移对三维点位置的偏导数。运动场是三维运动在图像平面上的理想二维表示，它是我们无法直接观察到的“真实值”；我们只能通过噪声观测（视频）估计光流（表观运动）。

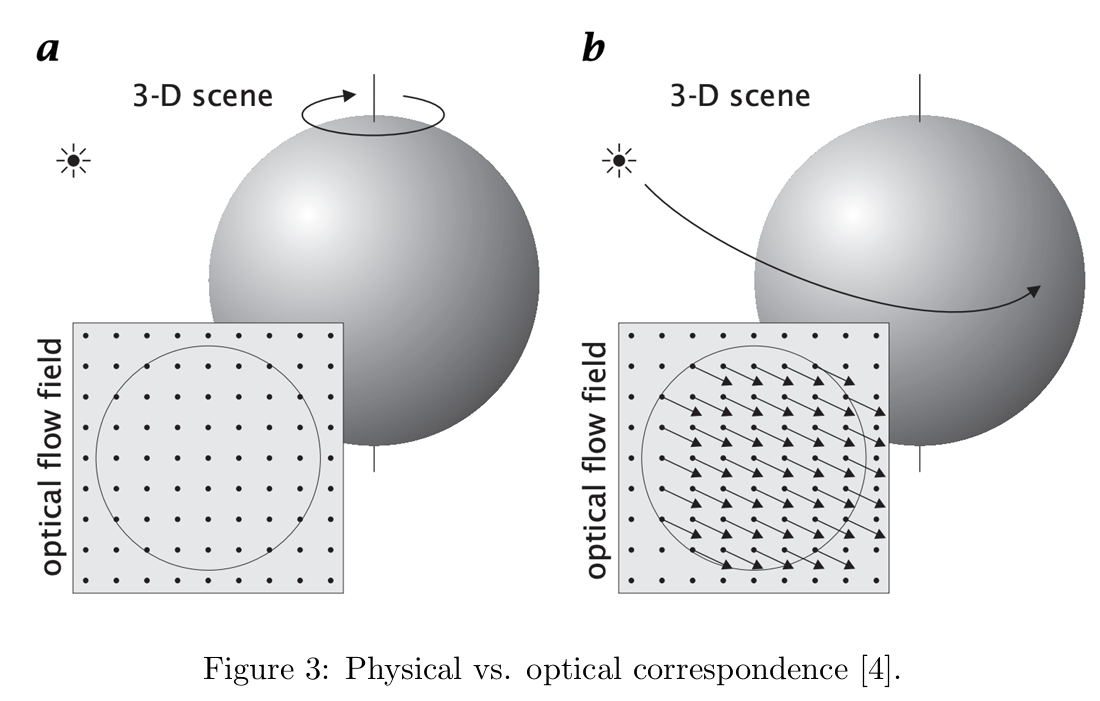
需要注意的是，光流并不总是等同于运动场。我们先假设观察相机是一个独立固定的能够观察到光源和球体。
例如，一个带有固定光源的均匀旋转球体没有光流，但其运动场不为零。（场景的亮度不会变化，因此观察不到像素的运动，光流为零；但是从物理上来看，球体确实在运动，存在真实的三维运动，运动场不为零）
相反，一个固定的均匀球体在光源周围运动时，光流非零但运动场为零。这两种情况如图3所示。（随着光源移动，球体的亮度分布发生了变化，因此像素看起来像是在“运动”，光流不为零；然而，实际上球体并没有发生任何实际运动，运动场为零）

计算光流

我们将一个视频定义为按照时间顺序排列的一系列帧。像素 $(x, y)$ 在时间 $t$ 时的亮度用函数 $I(x, y, t)$ 表示。在稠密光流（Dense Optical Flow）中，我们希望在每个时间点 $t$ 为每个像素 $(x, y)$ 计算其在 $x$ -轴和 $y$ -轴上的表观速度，分别用 $u(x, y, t) = \frac{\Delta x}{\Delta t}$ 和 $v(x, y, t) = \frac{\Delta y}{\Delta t}$ 表示。于是，每个像素的光流向量可写为：

$u = \begin{bmatrix} u \\ v \end{bmatrix}.$

接下来的部分中，我们将描述Lucas-Kanade方法，它是一种通过最小二乘法，在局部像素块内独立求解光流的方法。

亮度恒常性假设

基于亮度恒常性假设，我们可以认为同一物体在图像平面上的表观亮度不会随帧变化而改变。用方程表示，对于一个像素在时间 $t$ 到 $t + \Delta t$ 之间在 $x$ 和 $y$ 方向上分别移动 $\Delta x$ 和 $\Delta y$ 时，有：

$I(x, y, t) = I(x + \Delta x, y + \Delta y, t + \Delta t).$

一种常见的简化是假设 $\Delta t = 1$ （即相邻帧之间的时间间隔为1），因此像素的速度等于其位移，即 $u = \Delta x$ ， $v = \Delta y$ 。于是可以写成：

$I(x, y, t) = I(x + u, y + v, t + 1).$

小位移假设

泰勒展开补充

基于小位移假设，我们假设每帧之间的像素位移 $(\Delta x, \Delta y)$ 很小。这样我们可以用一阶泰勒展开对亮度函数 $I$ 进行线性化，如下所示：

$I(x + \Delta x, y + \Delta y, t + \Delta t) \approx I(x, y, t) + \frac{\partial I}{\partial x}\Delta x + \frac{\partial I}{\partial y}\Delta y + \frac{\partial I}{\partial t}\Delta t.$

将这一展开式代入亮度恒常性假设的方程中（即 $I(x, y, t) = I(x + \Delta x, y + \Delta y, t + \Delta t)$ ），可以得到光流约束方程：

$0 = \frac{\partial I}{\partial x} \Delta x + \frac{\partial I}{\partial y} \Delta y + \frac{\partial I}{\partial t} \Delta t.$

进一步简化后可得：

$I_x u + I_y v + I_t = 0,$

其中 $I_x$ 、 $I_y$ 、 $I_t$ 分别是亮度函数对 $x$ 、 $y$ 、 $t$ 的偏导数，分别代表亮度在空间和时间上的梯度。

我们将其简化为矩阵形式： $$ \begin{bmatrix} I_x & I_y \end{bmatrix} \begin{bmatrix} u \ v \end{bmatrix} = -I_t, $$ 或者： $$ \mathbf{\nabla} I^T \mathbf{u} = -I_t, $$ 其中 $\mathbf{\nabla} I = \begin{bmatrix} I_x \\ I_y \end{bmatrix}$ 是亮度的空间梯度， $\mathbf{u} = \begin{bmatrix} u \\ v \end{bmatrix}$ 是待求解的光流向量。

欠约束系统的性质

由于亮度梯度 $\mathbf{\nabla} I$ 是一个二维向量场，而我们需要同时解 $u$ 和 $v$ ，所以这是一种欠约束的系统。即使增加光流约束方程，我们仍然只有一个方程来解决两个未知数。在这种情况下，光流约束方程仅能提供光流在亮度梯度方向上的分量（即法向光流）。如图 4 所示，光流约束方程的解集是一个直线，表示所有可能的 $(u, v)$ 组合。

光流与梯度方向的关系

回顾两个向量 $\mathbf{a}$ 和 $\mathbf{b}$ 的点积定义： $$ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}||\mathbf{b}| \cos(\theta), $$
其中 $\theta$ 是两个向量之间的夹角。通过点积公式，可以将光流投影到梯度方向上，表示为：

$\frac{\mathbf{\nabla} I}{\|\mathbf{\nabla} I\|} \cdot \mathbf{u} = \frac{-I_t}{\|\mathbf{\nabla} I\|}.$

公式表明，光流约束只能提供法向分量，而缺少沿图像边缘方向的分量。

图 5 展示了一个示例图像中 x 和 y 方向上的空间梯度。可以看到，高梯度幅值对应于图像的边缘。

其中，左侧图是灰度图，中间是图像在x轴的梯度图（梯度反映的是像素亮度变化的快慢；如果亮度变化剧烈（例如边缘位置），梯度值较高（通常以黑或白表示）），右侧是y的梯度图

光流约束的法向分量

下方公式显示了光流约束如何提供 $\mathbf{u}$ 在 $\nabla I$ 上的投影，这被称为法向光流（Normal Flow）：

$\frac{\nabla I}{\|\nabla I\|} \cdot \mathbf{u} = \frac{-I_t}{\|\nabla I\|}.$

光流约束的解集

图 4 展示了光流约束方程的解集，它是一条形如 $y = mx + b$ 的直线。这条直线表示所有可能的光流向量 $(u, v)$ 组合，它们满足光流约束方程。

此外，我们还可以将这些解与图像空间对应起来。法向光流的方向与给定像素亮度梯度的空间方向一致。在图像空间中，解集的方向与图像边缘一致，因为法向光流与亮度梯度正交。

因此，虽然我们知道光流向量在梯度方向上的分量（法向光流），但无法确定沿着图像边缘方向的分量。这些不确定性形成了解集（直线），其可能的值由沿边缘方向的自由度表示。

孔径问题（Aperture Problem）

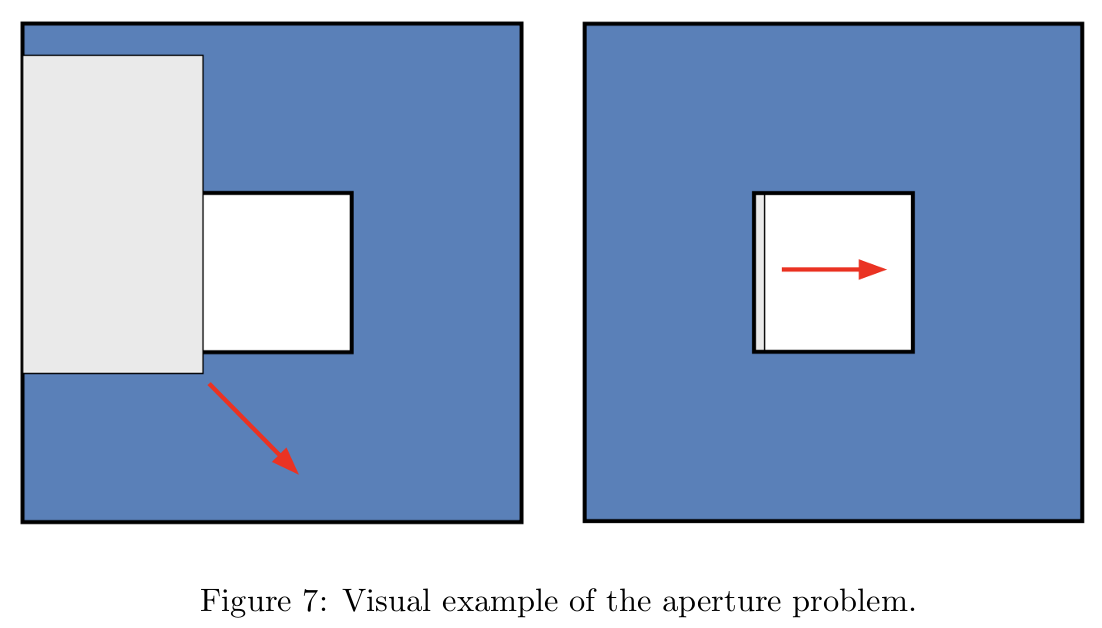
这种无法确定边缘方向上光流分量的问题被称为孔径问题，图 7 中对此进行了说明：

图左侧：一个灰色矩形完全暴露于视野中，其运动方向可以清楚地被观察到。
图右侧：当灰色矩形被蓝色方块遮挡时，仅能看到矩形通过孔径的亮度梯度方向上的运动，即法向运动（normal motion）。然而，无法确定它在图像边缘方向上的实际运动。

这是因为我们只能测量亮度梯度方向上的分量，而图像边缘方向上的运动信息丢失了。

缓解孔径问题：空间平滑性假设

为了解决孔径问题，我们引入了空间平滑性假设：假设图像中邻近的像素属于同一表面，因此具有相同的光流。这一假设使我们可以通过使用像素邻域的信息来增加约束条件。

假设当前像素周围有一个 $N \times N$ 的邻域，我们可以为该邻域内的每个像素 $p_i = [x_i, y_i]^T$ 写出光流约束方程：

$\mathbf{A}\mathbf{u} = \mathbf{b},$

其中：

$\mathbf{A} = \begin{bmatrix} I_x(p_1) & I_y(p_1) \\ \vdots & \vdots \\ I_x(p_{N^2}) & I_y(p_{N^2}) \end{bmatrix}, \quad \mathbf{b} = - \begin{bmatrix} I_t(p_1) \\ \vdots \\ I_t(p_{N^2}) \end{bmatrix}.$

这样，我们为邻域内每个像素引入了一个新的约束条件，从而使系统变得可解，可见这是一个非齐次线性方程组，使用最小二乘法求解。

最小二乘解法

通过最小化误差 $\|\mathbf{A}\mathbf{u} - \mathbf{b}\|$ ，我们得到最小二乘解：

$\mathbf{u}_{\text{ls}} = (\mathbf{A}^T\mathbf{A})^{-1}\mathbf{A}^T\mathbf{b}.$

这种方法有效地利用了像素邻域的信息来估算光流，缓解了孔径问题带来的自由度不足问题。

增加邻域约束的条件

为了确保引入邻域后，光流约束系统能够可靠地求解，以下条件需要满足：

$\mathbf{A}^T \mathbf{A}$ 的值不能太小：
- 如果像素所在区域的梯度幅值较小（例如低纹理区域），则 $\mathbf{A}^T \mathbf{A}$ 的特征值会很小，导致解容易受到噪声干扰。
$\mathbf{A}^T \mathbf{A}$ 必须条件良好（well-conditioned）：
- 如果图像区域的梯度主要集中在某一个方向（例如在边缘处，梯度向量指向相同方向）， $\mathbf{A}^T \mathbf{A}$ 的一个特征值可能比另一个大得多，系统的条件数会很大。这种情况下，解的稳定性较差。

理想的求解区域

最佳的光流估算区域是具有高纹理并且空间结构方向多样化的区域。这些区域的特点是：

存在多个梯度方向（例如角点），导致 $\mathbf{A}^T \mathbf{A}$ 的两个特征值均较大且接近，系统条件良好，解的稳定性更高。

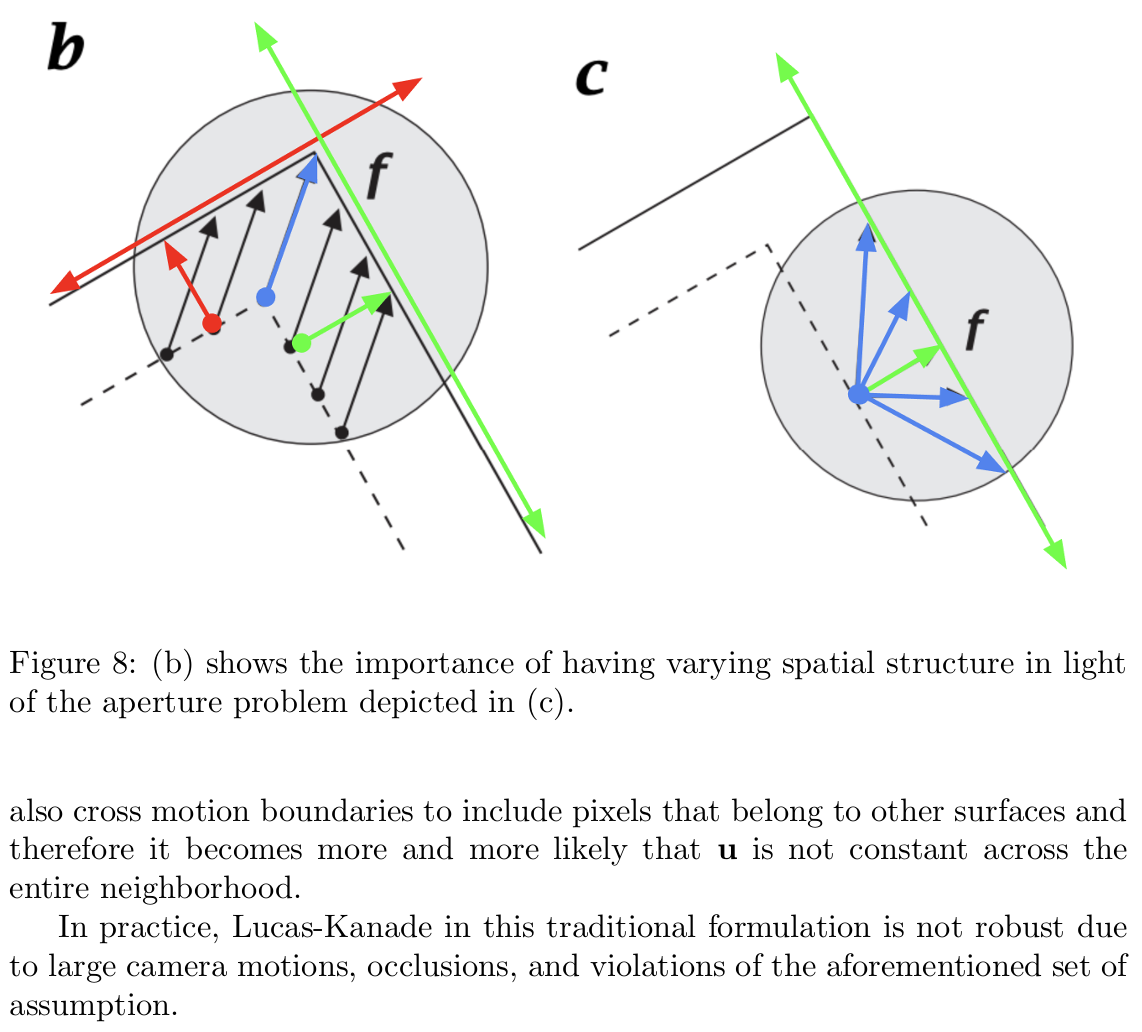
为了更直观地理解方向多样性的好处，可以参考图 8：

©：仅有一个法向光流矢量（绿色），对应一条解集直线，可能的解数量较多。
(b)：角点区域包含多个梯度方向（例如红色和绿色的梯度向量），对应两条解集直线，其交点为唯一的解。

邻域大小的权衡

增大邻域大小 $N$ 会增加包含更多方向信息的机会，从而提高解的准确性。然而，邻域大小的增大会带来以下问题：

跨越运动边界：邻域可能包含来自不同表面的像素，导致光流不一致。
解的偏差：跨越运动边界的邻域可能引入干扰，使得光流估算偏离真实值。

Lucas-Kanade 方法的局限性

尽管传统的 Lucas-Kanade 方法在小运动和局部平滑的假设下表现良好，但在以下情况中，其鲁棒性较差：

大范围的相机运动：局部假设被破坏，梯度方向信息不足。
遮挡问题：邻域内的像素可能消失或被遮挡。
假设的违背：场景中的表面可能不是平滑的，导致邻域内光流不一致。

状态最优估计

状态估计

了解环境的当前状态对于人工智能代理可靠地进行实时决策非常重要。在状态估计中，我们的目标是通过持续整合来自不同传感器的测量数据（多模态感知），推断出系统在当前时刻的潜在状态。

我们首先从概率的角度研究离散时间动态系统。图1以图模型的形式展示了一个部分可观测的马尔科夫决策过程（POMDP）。

图1：部分可观测马尔科夫决策过程（POMDP）的图模型。

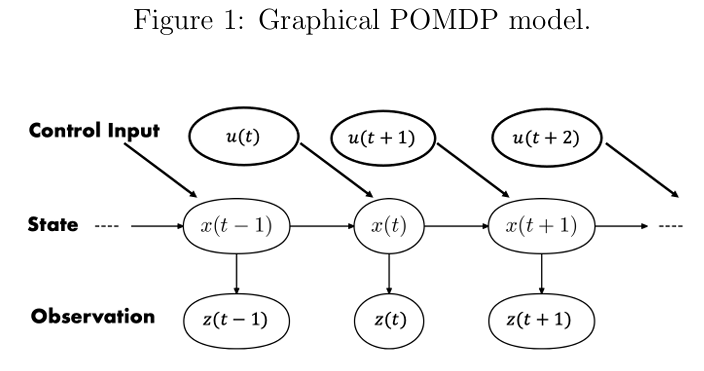
有向边表示条件依赖关系。时间 $t$ 的状态 $x_t \in \mathbb{R}^n$ 仅依赖于之前的状态 $x_{t-1}$ 。时间 $t$ 的传感器观测值 $z_t \in \mathbb{R}^k$ 依赖于时间 $t$ 的状态。时间 $t$ 的控制输入 $u_t \in \mathbb{R}^m$ 表示应用于系统的控制。例如，处于某种环境中的人工智能代理的状态可以是位置、方向、线速度和角速度，或上述任意组合。类似地，从状态派生的测量值可以是环境的相机图像或激光雷达数据，这些数据依赖于机器人的位置和运动。

测量值和控制输入是已知的，但隐藏状态历史 $x_{0:t}$ 是未知的。我们假设系统以随机的方式演化，观测值也是随机的。因此，我们将状态 $X_t$ 和观测值 $Z_t$ 建模为随机变量，它们可以分别取 $x_t$ 和 $z_t$ 的值。为了简化符号，我们用 $p(X_t = x_t)$ 表示 $p(x_t)$ ，对 $Z_t$ 也是类似。

状态估计器的目标是计算或逼近在已知数据（测量值和控制输入的历史）及状态转移和观测模型的基础上，状态 $x_t$ 的后验概率分布。具体而言，我们想知道状态的后验分布 $p(x_t|z_{1:t}, u_{1:t})$ ，它为每一个可能的状态值分配一个概率，条件是给定测量值和控制输入的序列。后验分布也被称为时间 $t$ 状态值的信念，用 $\text{bel}(t)$ 表示。概率形式不能给出状态的确切值，但能让我们量化对状态可能值的不确定性。

通过使用图1中的图模型表示动态系统，我们假设状态是完整的。这个假设导致了两个关键属性。首先，我们假设系统是马尔可夫的，即当前状态 $x_t$ 仅依赖于前一个状态 $x_{t-1}$ 和前一个控制输入 $u_{t-1}$ ，而不是整个历史 $z_{1:t-1}$ 。这可以表示为：

$p(x_t|x_{0:t-1}, z_{1:t-1}, u_{1:t}) = p(x_t|x_{t-1}, u_t)$

这也称为转移模型，表示系统从当前状态 $x_{t-1}$ 转移到状态 $x_t$ 的可能性，条件是给定控制输入 $u_t$ 。

其次，我们假设当前测量值 $z_t$ 仅依赖于当前状态 $x_t$ ，即 $z_t$ 在条件上独立于所有先前的状态 $x_{0:t-1}$ 、测量值 $z_{1:t-1}$ 和控制输入 $u_{1:t}$ 。这可以表示为：

$p(z_t|x_{0:t}, z_{1:t-1}, u_{1:t}) = p(z_t|x_t)$

这也被称为测量模型，表示给定状态 $x_t$ ，测量值 $z_t$ 的可能性。

贝叶斯滤波器（Bayes Filter）

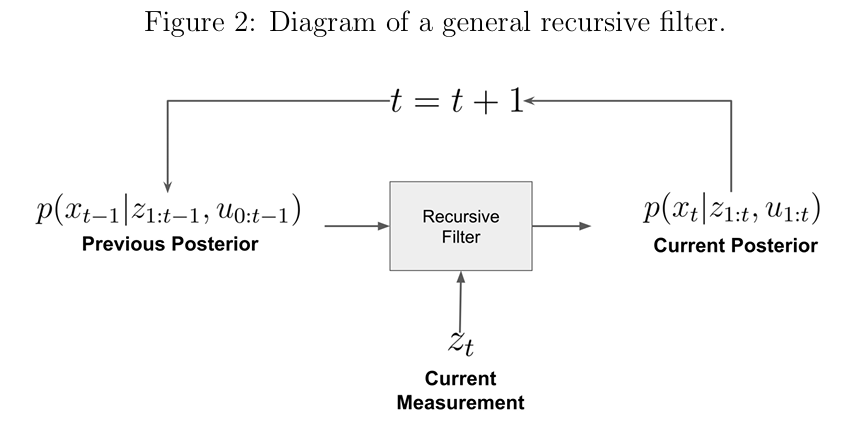
递归滤波器通过不断地吸收新的测量值来估计状态的后验分布，如图2所示。在每个时间步 $t$ ，我们只使用旧的后验分布 $p(x_{t-1}|z_{1:t-1}, u_{0:t-1})$ 、新的控制输入 $u_{t-1}$ 和新的测量值 $z_t$ 来计算新的后验分布 $p(x_t|z_{1:t}, u_{0:t})$ 。因此，递归滤波器的复杂度与时间无关；它不依赖于历史数据的大小，非常适合实时推断。

图2：通用递归滤波器的示意图

条件概率回顾

我们可以通过如下公式分解联合概率分布：

$p(A,B) = p(A|B)p(B)$

其中 $A$ 和 $B$ 是随机变量。如果联合分布被条件化到另一个随机变量 $C$ ，我们可以传递条件化信息：

$p(A,B|C) = p(A|B,C)p(B|C)$

边缘化分布的公式为：

$p(A) = \int_B p(A,B) dB$

类似地，对于条件概率：

$p(A|C) = \int_B p(A,B|C) dB$

通过两种方式分解联合分布，可以得到贝叶斯定理：

$p(A|B)p(B) = p(B|A)p(A)$

推导

我们现在推导贝叶斯滤波器，这是最简单的递归滤波器。我们的目标是推导一个递归公式，用于计算状态的后验分布，该公式只依赖于先前的后验分布、当前的测量值 $z_t$ 、控制输入 $u_t$ ，以及已知的状态转移和测量模型。假设这些模型是已知且可计算的，即 $p(x_t|x_{t-1}, u_t)$ 和 $p(z_t|x_t)$ 。通过贝叶斯定理和测量值的条件独立性，我们可以得到：

$(x_t|z_{1:t}, u_{1:t}) = \frac{p(z_t|x_t, z_{1:t-1}, u_{1:t})p(x_t|z_{1:t-1}, u_{1:t})}{p(z_t|z_{1:t-1}, u_{1:t})}$

利用测量值的条件独立性假设：

$p(z_t|x_t, z_{1:t-1}, u_{1:t}) = p(z_t|x_t)$

简化后，公式变为：

$p(x_t|z_{1:t}, u_{1:t}) = \frac{p(z_t|x_t)p(x_t|z_{1:t-1}, u_{1:t})}{p(z_t|z_{1:t-1}, u_{1:t})}$

我们现在简化分母 $p(z_t|z_{1:t-1}, u_{1:t})$ 和分子中的 $p(x_t|z_{1:t-1}, u_{1:t})$ 。

分母的简化：

通过边缘化 $x_t$ 并利用测量值的条件独立性：

$p(z_t|z_{1:t-1}, u_{1:t}) = \int_{x_t} p(z_t, x_t|z_{1:t-1}, u_{1:t}) dx_t \\ = \int_{x_t} p(z_t|x_t, z_{1:t-1}, u_{1:t}) p(x_t|z_{1:t-1}, u_{1:t}) dx_t \\ = \int_{x_t} p(z_t|x_t) p(x_t|z_{1:t-1}, u_{1:t}) dx_t$

分子的先验分布

$p(x_t|z_{1:t-1}, u_{1:t})$ ：

通过边缘化 $x_{t-1}$ 并应用马尔可夫假设：

$p(x_t|z_{1:t-1}, u_{1:t}) = \int_{x_{t-1}} p(x_t, x_{t-1}|z_{1:t-1}, u_{1:t}) dx_{t-1} \\ = \int_{x_{t-1}} p(x_t|x_{t-1}, z_{1:t-1}, u_{1:t}) p(x_{t-1}|z_{1:t-1}, u_{1:t}) dx_{t-1} \\ = \int_{x_{t-1}} p(x_t|x_{t-1}, u_t) p(x_{t-1}|z_{1:t-1}, u_{1:t}) dx_{t-1}$

将所有部分结合后，我们得到贝叶斯滤波器的完整形式。

图3：贝叶斯滤波器的示意图

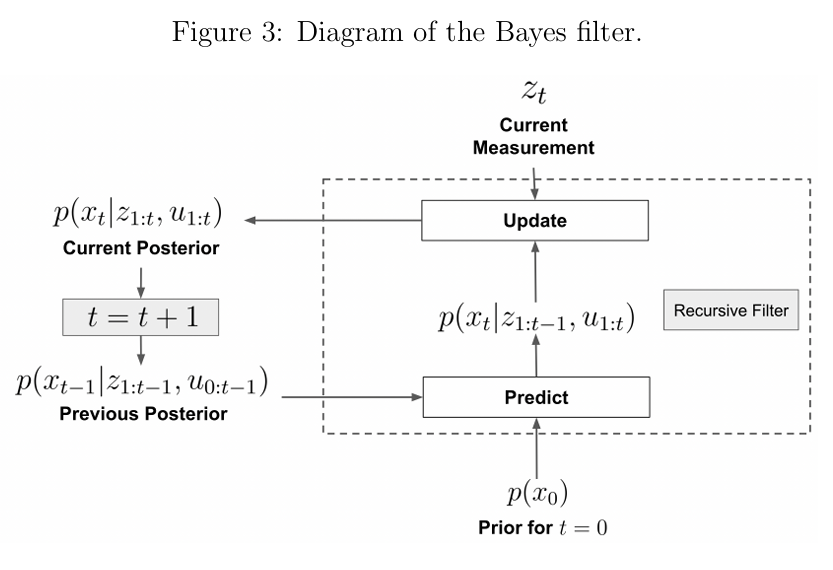
图4：贝叶斯滤波器的预测和更新步骤公式

2.3 离散贝叶斯滤波器

我们来看一个离散情况下的实际实现，其中 $X_t$ 和 $Z_t$ 都只有有限个可能值。假设 $X_t$ 是一个离散随机变量，有 $N$ 个可能值； $X_t$ 的域为 $x_t \in \{1, 2, \ldots, N\}$ 。同样， $Z_t$ 是一个离散随机变量，有 $M$ 个可能值； $Z_t$ 的域为 $z_t \in \{1, 2, \ldots, M\}$ 。对于离散贝叶斯滤波器，预测和更新的公式与连续情况相同，但积分被替换为求和。

信念向量（即状态后验分布）的公式如下：

$\text{bel}(t) = \begin{pmatrix} p(X_t = 1|z_{1:t}, u_{1:t}) \\ p(X_t = 2|z_{1:t}, u_{1:t}) \\ \vdots \\ p(X_t = N|z_{1:t}, u_{1:t}) \end{pmatrix}$

预测步骤可表示为矩阵乘法：

$\hat{\text{bel}}(t) = T(u_t) \text{bel}(t-1)$

其中， $T(u_t)$ 表示转移概率矩阵，形式为：

$T(u_t) = \begin{pmatrix} p(X_t = 1|X_{t-1} = 1, u_t) & \cdots & p(X_t = 1|X_{t-1} = N, u_t) \\ \vdots & \ddots & \vdots \\ p(X_t = N|X_{t-1} = 1, u_t) & \cdots & p(X_t = N|X_{t-1} = N, u_t) \end{pmatrix}$

更新步骤也可以通过矩阵乘法实现：

$\text{bel}(t) = \frac{M(z_t) \hat{\text{bel}}(t)}{\mathbf{1}^\top M(z_t) \hat{\text{bel}}(t)}$

其中， $M(z_t)$ 是测量模型的概率矩阵：

$M(z_t) = \begin{pmatrix} p(Z_t = 1|X_t = 1) & \cdots & p(Z_t = 1|X_t = N) \\ \vdots & \ddots & \vdots \\ p(Z_t = M|X_t = 1) & \cdots & p(Z_t = M|X_t = N) \end{pmatrix}$

分母中的 $\mathbf{1}^\top$ 是一个向量，所有元素为1，用于对未归一化的概率求和。

卡尔曼滤波器（Kalman Filter）

之前，我们看到了状态转移模型 $p(x_t|x_{t-1}, u_t)$ 和测量模型 $p(z_t|x_t)$ 的概率表示方法。这是贝叶斯的视角。状态转移和测量模型也可以从动态系统的视角来看，分别由以下方程表示动态模型和测量模型：

$x_t = f(x_{t-1}, u_t) + w_{t-1} \\ z_t = h(x_t) + v_t$

其中：

$f(\cdot)$ 表示系统的动态规律，描述状态从 $x_t$ 到 $x_{t+1}$ 的演化方式。
$h(\cdot)$ 是一个映射函数，将状态 $x_t$ 映射到对应的观测值。
$w_t$ 和 $v_t$ 分别是过程噪声和测量噪声，这些噪声是动态系统中自然存在的随机扰动。

我们假设动态模型、测量模型以及噪声的统计特性 $D_w$ 和 $D_v$ 是已知的，其中 $w \sim D_w$ 且 $v \sim D_v$ 。这些动态系统方程与图1中的图模型一致，并符合我们关于状态是完整的假设：即 $x_t$ 仅依赖于 $x_{t-1}$ 和 $u_t$ ，而 $z_t$ 仅依赖于 $x_t$ 。

高斯分布（Gaussian Distributions）

如果 $X \in \mathbb{R}^N$ 是从多元高斯分布（又称正态分布）中采样的随机向量，我们表示为 $X \sim \mathcal{N}(\mu, \Sigma)$ ，其中：

$\mu \in \mathbb{R}^N$ 是均值向量。
$\Sigma \in \mathbb{R}^{N \times N}$ 是正定的协方差矩阵（在一元情况下相当于方差）。

对应的概率密度函数（PDF）为：

$p(X) = \frac{1}{\sqrt{(2\pi)^N |\Sigma|}} \exp\left(-\frac{1}{2}(x - \mu)^T \Sigma^{-1} (x - \mu)\right) \tag{13}$

图5：左图展示了多元高斯分布的形状；右图展示了等概率轮廓线（等高线）。

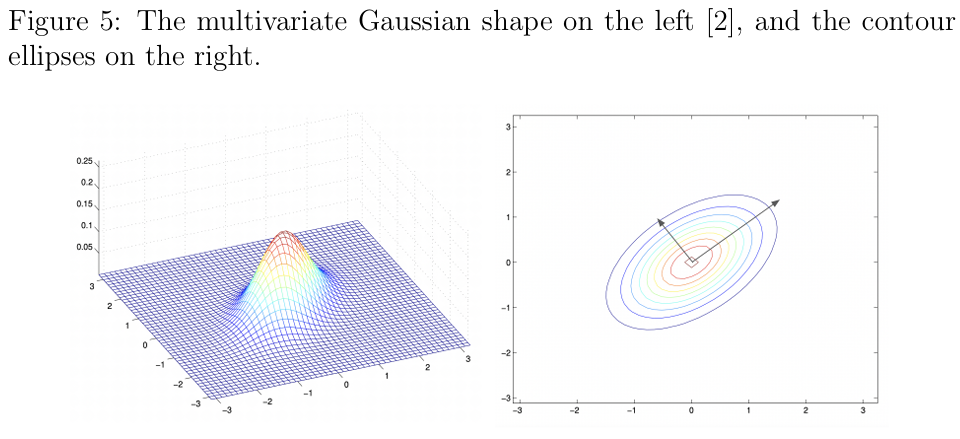
协方差矩阵 $\Sigma$ 表示分布在每个方向上的“扩展程度”：

$\Sigma$ 的特征向量是分布的主轴方向。
特征值表示对应方向上的不确定性大小。大的特征值表明在对应方向上有更大的不确定性，而小的特征值则相反。

协方差矩阵不仅表示分布的置信度，还间接捕获了状态的不同分量之间的相关性，这在估计中非常有用。

卡尔曼滤波器的基本假设

卡尔曼滤波器是贝叶斯滤波器在线性高斯系统上的应用。正如其名称所暗示的，线性高斯系统有两个关键假设：

所有涉及的随机变量（如状态、测量值、后验分布、噪声）均为多元高斯分布。
所有变量与其父变量的关系均为线性关系，即 $f(\cdot)$ 和 $h(\cdot)$ 是线性的，形如 $y = Ax$ 。

线性高斯系统的动态模型和测量模型分别为：

$x_t = A_t x_{t-1} + B_t u_t + w_t \\ z_t = C_t x_t + v_t$

其中：

$w_t \sim \mathcal{N}(0, Q_t)$ ：过程噪声，服从零均值高斯分布，协方差矩阵为 $Q_t$ 。
$v_t \sim \mathcal{N}(0, R_t)$ ：测量噪声，服从零均值高斯分布，协方差矩阵为 $R_t$ 。

我们还假设：

$w_t$ 和 $v_t$ 是彼此独立的。
$w_t$ 和 $v_t$ 在时间上不相关，即 $\text{Cov}(w_t, w_\tau) = 0$ 和 $\text{Cov}(v_t, v_\tau) = 0$ 当 $t \neq \tau$ 时。

初始条件或先验表示为：

$x_0 \sim \mathcal{N}(\mu_{0|0}, \Sigma_{0|0})$

此外，假设 $x_0$ 与 $v_t$ 和 $w_t$ 相互独立。

卡尔曼滤波器的核心思想

虽然卡尔曼滤波器局限于线性高斯系统，但它可以高效地处理连续随机变量和向量（无限多种可能值）。这是因为只要我们知道均值 $\mu$ 和协方差 $\Sigma$ ，我们就可以完全描述概率分布。因此，与贝叶斯滤波器需要更新整个分布 $p(x)$ （对所有可能的 $x$ ），卡尔曼滤波器只需更新均值向量和协方差矩阵即可，这可以通过闭式公式实现。

卡尔曼滤波器与贝叶斯滤波器类似，也由**预测（Predict）和更新（Update）**两个步骤组成。

预测步骤（Predict Step）

在预测步骤中，我们根据系统的过程模型，利用先前的后验分布计算当前时刻的预测后验分布：

$\mu_{t|t-1} = A_t \mu_{t-1|t-1} + B_t u_t \tag{16} \\ \Sigma_{t|t-1} = A_t \Sigma_{t-1|t-1} A_t^T + Q_t$

解释：

$\mu_{t|t-1}$ 是当前状态的预测均值，由先前状态均值通过状态转移方程预测得到。
$\Sigma_{t|t-1}$ 是当前状态的预测协方差，通过状态转移的线性变换叠加过程噪声协方差 $Q_t$ 得到。

更新步骤（Update Step）

在更新步骤中，我们利用新的测量值 $z_t$ 来修正预测的均值和协方差。更新公式如下：

$\mu_{t|t} = \mu_{t|t-1} + K_t(z_t - C_t \mu_{t|t-1}) \\ \Sigma_{t|t} = \Sigma_{t|t-1} - K_t C_t \Sigma_{t|t-1} \\ K_t = \Sigma_{t|t-1} C_t^T (C_t \Sigma_{t|t-1} C_t^T + R_t)^{-1}$

解释：

均值更新公式：
- $z_t$ 是传感器的实际测量值。
- $C_t \mu_{t|t-1}$ 是基于预测的测量值。
- $z_t - C_t \mu_{t|t-1}$ 是测量残差（也称为创新），表示预测的测量值与实际测量值之间的差距。
- 均值的更新试图利用测量残差来校正预测均值 $\mu_{t|t-1}$ ，权重由卡尔曼增益 $K_t$ 决定。
协方差更新公式：
- 卡尔曼增益 $K_t$ 用于修正预测协方差 $\Sigma_{t|t-1}$ 。
- 更新后的协方差 $\Sigma_{t|t}$ 通常会变小，表示通过结合测量值后对状态的不确定性减少了。
卡尔曼增益公式：
- 卡尔曼增益 $K_t$ 是一个权重，表示信任传感器测量值与预测状态的程度。
- 计算公式中的 $C_t \Sigma_{t|t-1} C_t^T + R_t$ 表示测量的不确定性总量，包括预测的测量不确定性和传感器噪声。

特殊情况分析：

为了更好地理解卡尔曼增益 $K_t$ ，我们分析两个极端情况：

测量噪声 $R_t$ 接近 0：
- 表明测量值非常可靠，几乎没有噪声。
- 此时 $K_t$ 接近 $C_t^{-1}$ ，均值更新为 $\mu_{t|t} = C_t^{-1} z_t$ ，即直接使用测量值来更新状态。
- 协方差 $\Sigma_{t|t}$ 接近 0，表示对状态的高度置信。
过程噪声 $\Sigma_{t|t-1}$ 接近 0：
- 表明预测状态非常精确。
- 此时 $K_t$ 接近 0，均值更新为 $\mu_{t|t} = \mu_{t|t-1}$ ，即完全忽略测量值。
- 这种情况下，过程模型已经足够描述状态的演化。

卡尔曼滤波器的整体流程

卡尔曼滤波器的整个过程交替执行预测步骤和更新步骤：

在预测步骤中，协方差通常增加，表示不确定性随着时间的推移而增加。
在更新步骤中，结合测量值减少协方差，表示不确定性降低。

这种协方差交替增加和减少的模式在多次迭代后最终会收敛。

图6：从分布视角看卡尔曼滤波器的更新过程

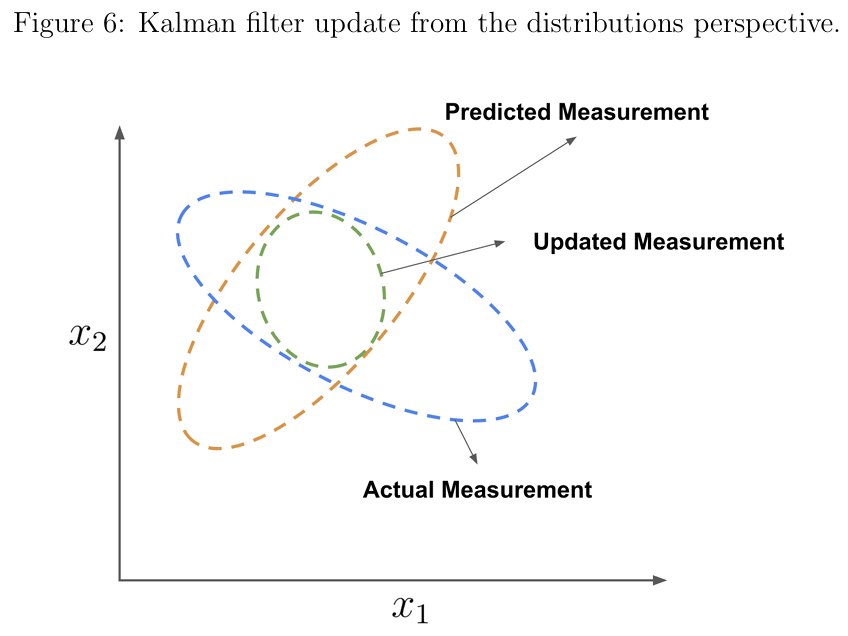
在图6中：

橙色椭圆表示预测的测量值分布（均值为 $C_t \mu_{t|t-1}$ ，协方差为 $C_t \Sigma_{t|t-1} C_t^T$ ）。
蓝色椭圆表示实际测量值分布（均值为 $z_t$ ，协方差为 $R_t$ ）。
绿色椭圆表示更新后的分布，即通过结合预测值和实际测量值后的状态分布。

注意：

预测步骤会增加协方差，表示不确定性上升。
更新步骤会减小协方差，表示通过新测量值减少了不确定性。

卡尔曼滤波器的局限性

卡尔曼滤波器适用于线性高斯系统，在以下场景可能受限：

系统或测量模型是非线性的。
状态或测量值的分布不是高斯分布。
噪声特性未知或变化。

接下来，如果需要处理非线性系统，可以使用扩展卡尔曼滤波器（Extended Kalman Filter, EKF）。

扩展卡尔曼滤波器（Extended Kalman Filter, EKF）

前面提到，卡尔曼滤波器适用于线性高斯系统。线性过程和测量模型保证了预测和更新后的分布仍为高斯分布。

图7：线性变换作用于高斯分布的示意图

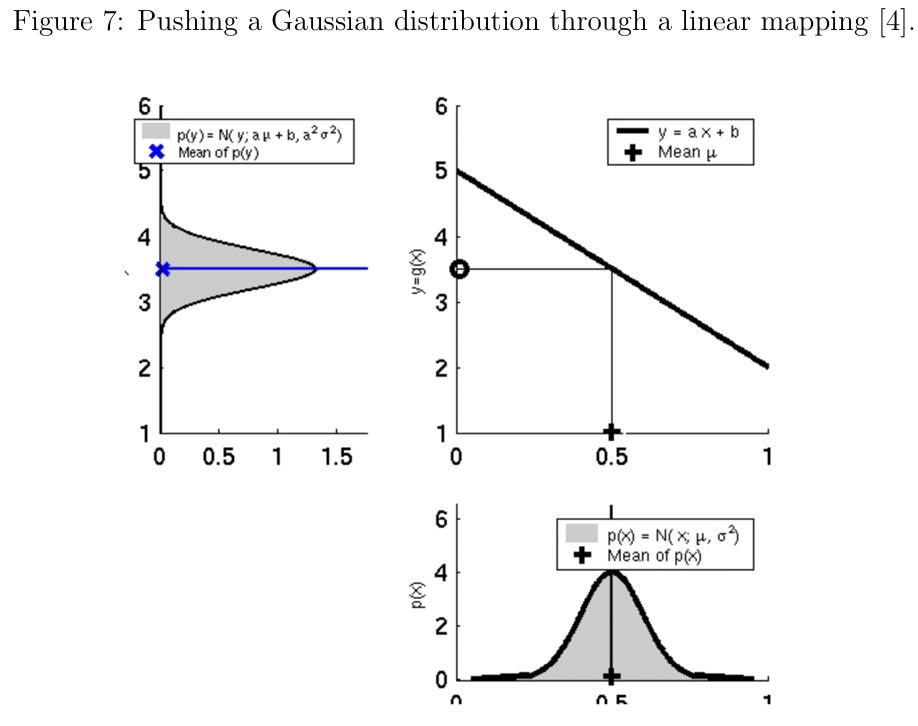
如图7所示，将线性变换作用于随机变量 $x$ 后，其结果仍是高斯分布。然而，图8展示了当作用非线性变换时，分布不再是高斯分布，此时原有的预测和更新公式不再适用。

图8：非线性变换作用于高斯分布的示意图

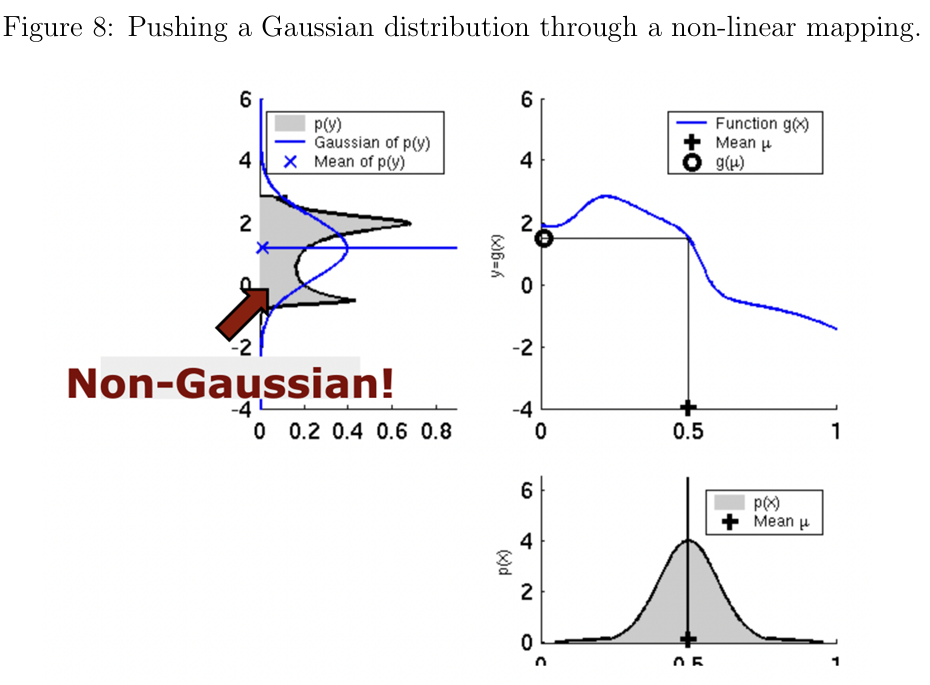
扩展卡尔曼滤波器通过在每个时间步 $t$ 对非线性动态和测量函数进行线性化，从而处理非线性系统。

线性化与泰勒展开

我们使用 一阶泰勒展开 在 $f(\mu_{t-1|t-1}, u_t)$ 和 $g(\mu_{t|t-1})$ 附近对非线性动态和测量模型进行线性化。

预测步骤

预测步骤的线性化公式为：

$\mu_{t|t-1} = f(\mu_{t-1|t-1}, u_t) \\ \Sigma_{t|t-1} = A_{t-1} \Sigma_{t-1|t-1} A_{t-1}^T + Q_{t-1}$

其中：

$A_t$ 是动态模型的雅可比矩阵，定义为：

$A_t(\mu_{t-1|t-1}, u_t) = \frac{\partial f(x_t, u_t)}{\partial x_t} \bigg|_{x_t = \mu_{t-1|t-1}}$

更新步骤

更新步骤的线性化公式为：

$\mu_{t|t} = \mu_{t|t-1} + K_t(z_t - g(\mu_{t|t-1})) \\ \Sigma_{t|t} = \Sigma_{t|t-1} - K_t C_t \Sigma_{t|t-1} \\ K_t = \Sigma_{t|t-1} C_t^T (C_t \Sigma_{t|t-1} C_t^T + R_t)^{-1}$

其中：

$C_t$ 是测量模型的雅可比矩阵，定义为：

$C_t(\mu_{t|t-1}, u_t) = \frac{\partial g(x_t)}{\partial x_t} \bigg|_{x_t = \mu_{t|t-1}}$

扩展卡尔曼滤波器的适用性

扩展卡尔曼滤波器适用于非线性系统，但其线性化近似可能引入误差，尤其是当非线性程度较大或状态远离线性化点时。

参考文献

[1] Chuong B Do. More on multivariate gaussians. URL http://cs229. stan ford. edu/section/more on gaussians. pdf.[Online], 2008.

[2] Chuong B Do. The multivariate gaussian distribution. Section Notes, Lecture on Machine Learning, CS, 229, 2008.

[3] Jonathan R. Shewchuk. Eigenvectors and the anisotropic multivariate normal distribution. Lecture Notes, CS, 189, 2019.

[4] Cyrill Stachniss. Extended kalman filter. http://ais.informatik. uni-freiburg.de/teaching/ws13/mapping/pdf/slam04-ekf.pdf, 2013. Accessed: 2022-01-31.