3D-Reconstruction
1.摄像机几何
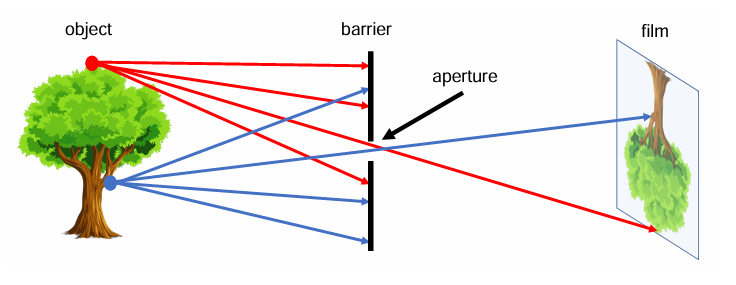
针孔模型
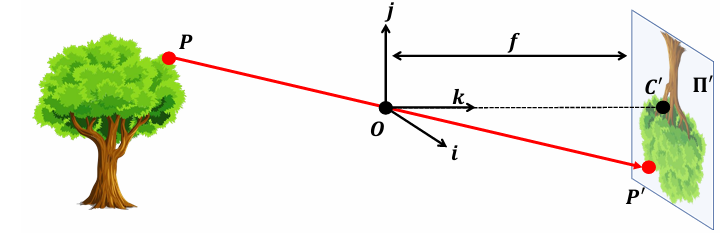
针孔相机的P与P^'^的映射关系:
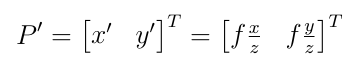
针孔模型的问题
光圈减小,成像更加清晰,但是光线减少,图像变暗
因此我们如何设计一个镜头,使得成像清晰,图像也足够亮。
解决方案就是增加透镜
透镜
透镜的性质:
平行于光轴的光线经过透镜会聚焦到焦点
穿过透镜中心的光线不发生偏转
因为穿过中心光线不偏转,因此我们可以把针孔相机的成像映射关系沿用到透镜模型中!
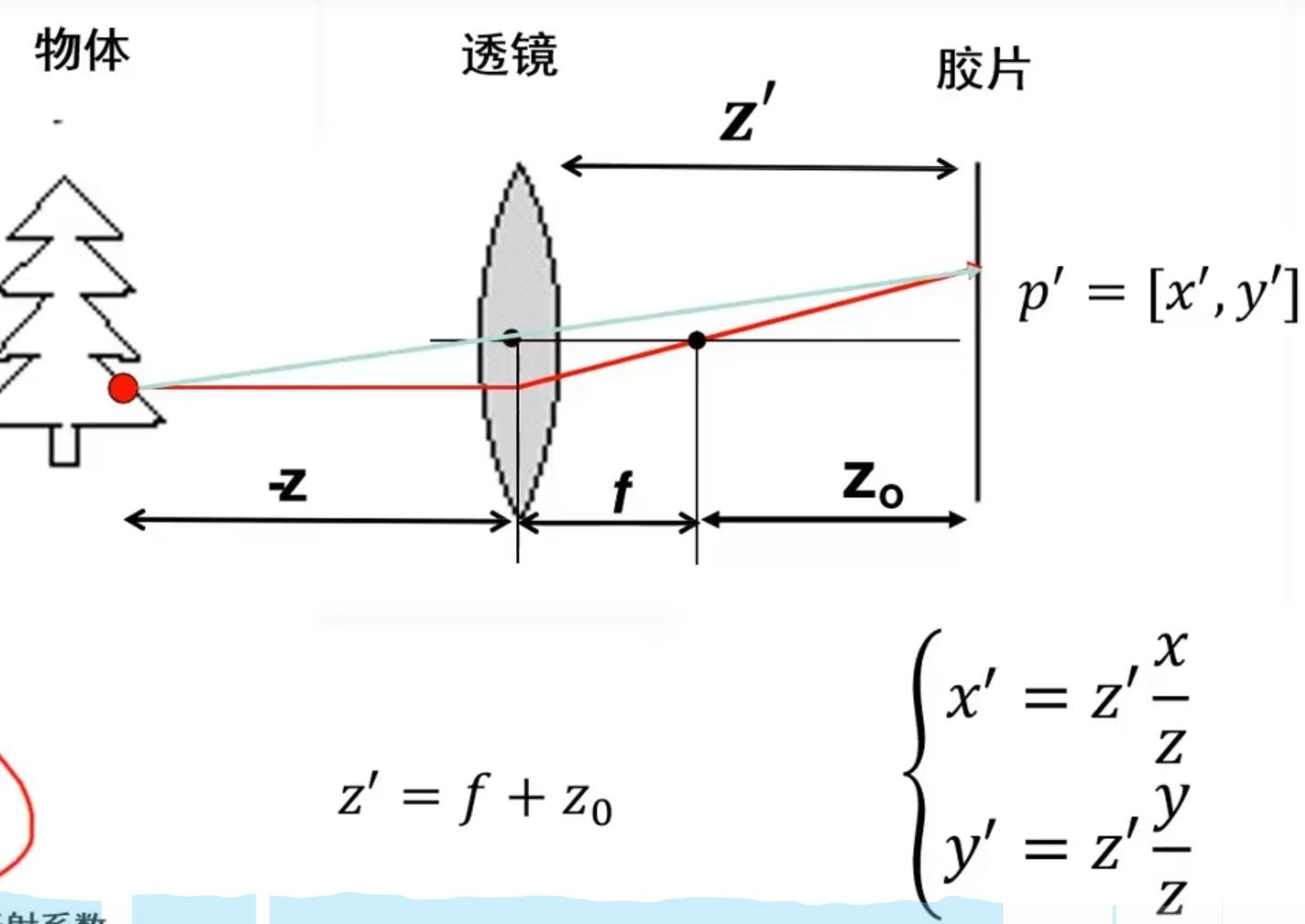
由于透镜是一个体积,而非一个点,根据Games101
有一个关系:
其中,f是焦距,z0是物距,z1是像距
因此某些过远或者过近的点出来的光线经过透镜会在成像平面形成一块区域而非一个点,这就是景深效果
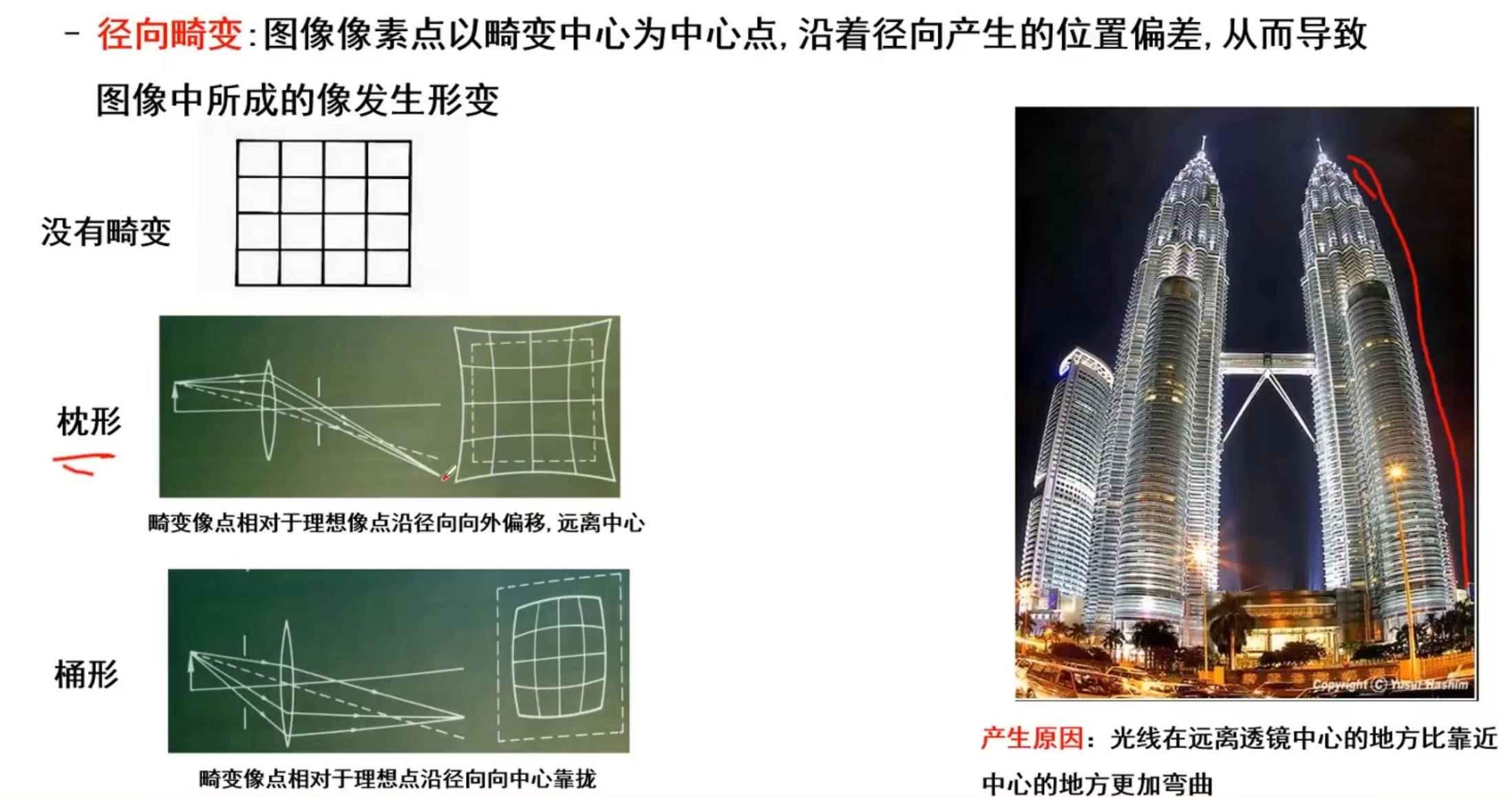
透镜的问题:径向畸变
摄像机几何
摄像机几何要处理的就是把一个世界空间的点映射到像素平面空间中
1.成像平面一般是图像中心为原点,像素平面通常是左下角为原点
加入一个位移变换:cx,cy
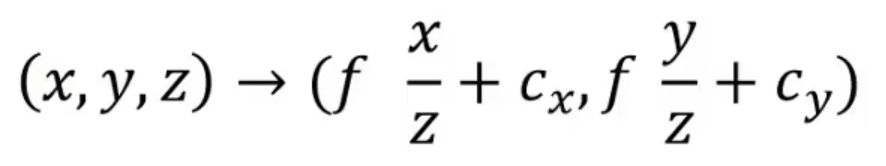
2.单位的变换
真实世界是连续的,以厘米为单位;像素图中是离散的,以像素pixel为单位
因此我们需要两个参数,表示x,y方向 从厘米到像素转换的单位变化率
k,l:pixel/cm
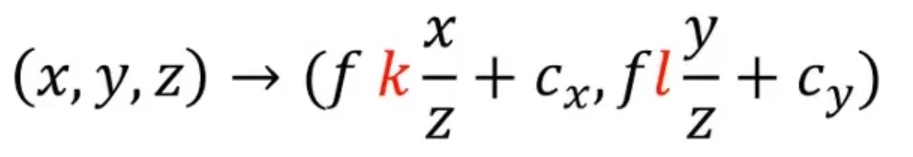
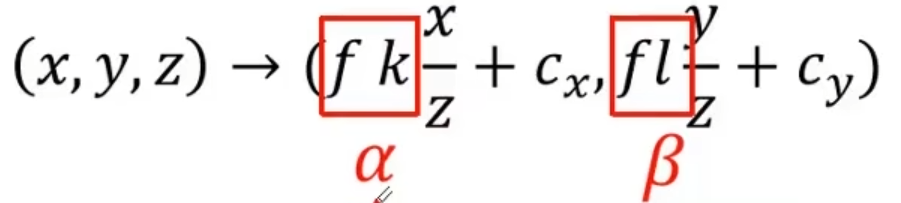
使用齐次坐标系把映射写为矩阵
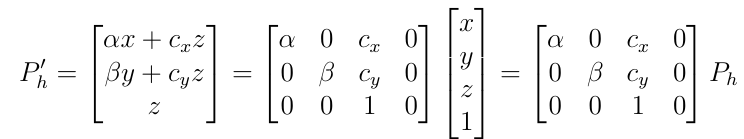
其中h下标表示在齐次坐标表示下
不过,课程说明,以后都去掉h,所有坐标都默认在齐次坐标下,除非特殊说明
成像平面x,y坐标非正交矩形的情况
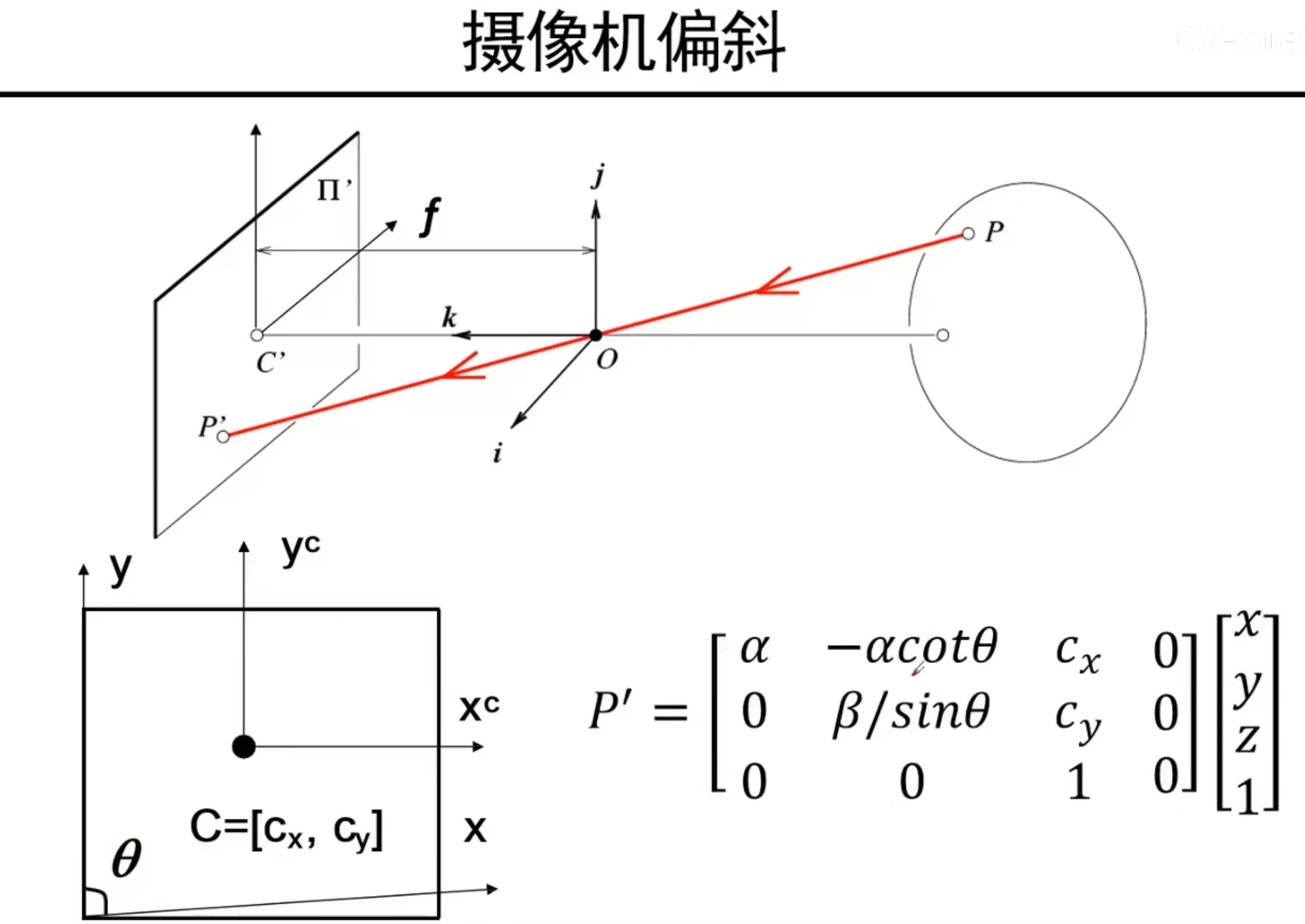
镜头制造工艺不好导致的夹角,引入一些角度偏移在我们的变换矩阵中
应该是成像平面相当于光轴的旋转角度
推导课程中未提及
3D世界到2D图像映射总结
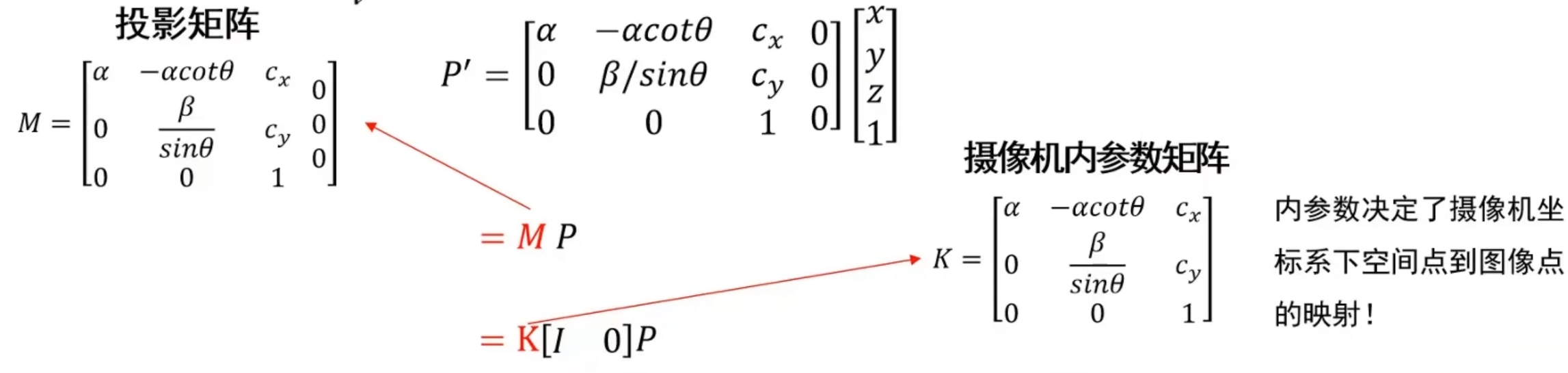
其中*[I 0]*的I是一个三行三列单位阵
其中,K矩阵有5个自由度(5 DOF)
因为K矩阵由5个变量决定
规范化摄像机
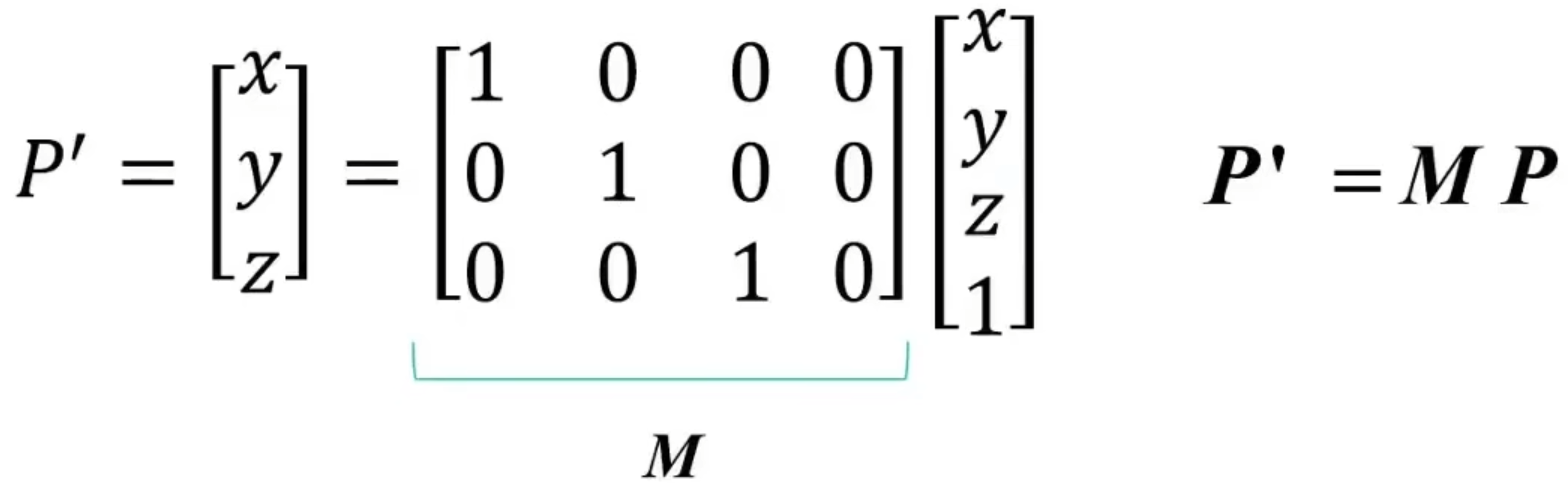
也就是说该相机是一个正方形标准相机,且像平面原点和像素平面原点一样
规范化相机的特点:二维点的齐次坐标加一维系数就可以得到三维世界的齐次坐标
从世界坐标到像素平面——投影矩阵的完整公式
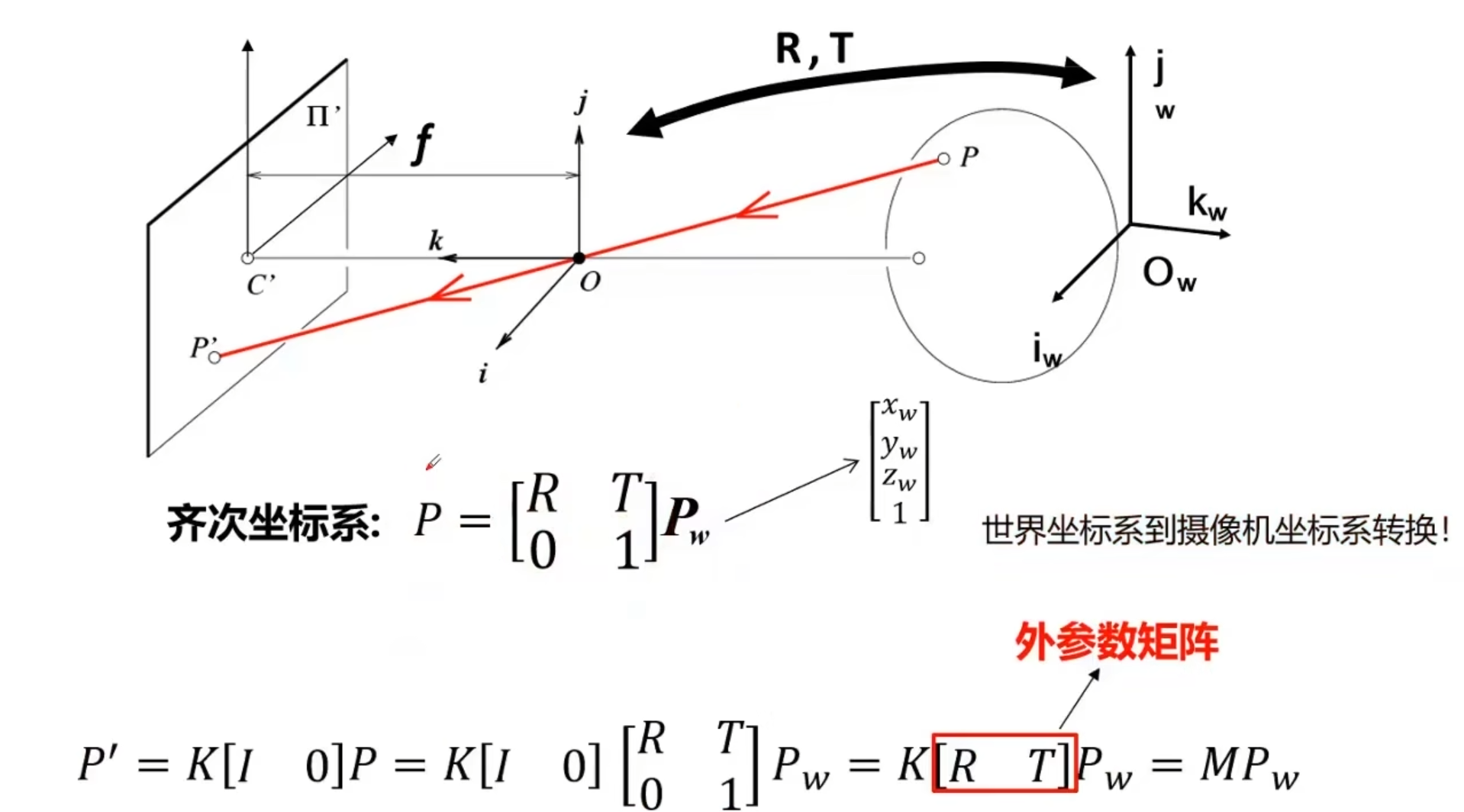
(图中的R是3x3旋转矩阵,T是3x1平移矩阵,I是3x3单位阵)
现在我们从世界空间Pw->相机空间P->成像平面->像素平面P^'^
简化后得到外参数矩阵[R T]和内参数矩阵K构成的投影矩阵
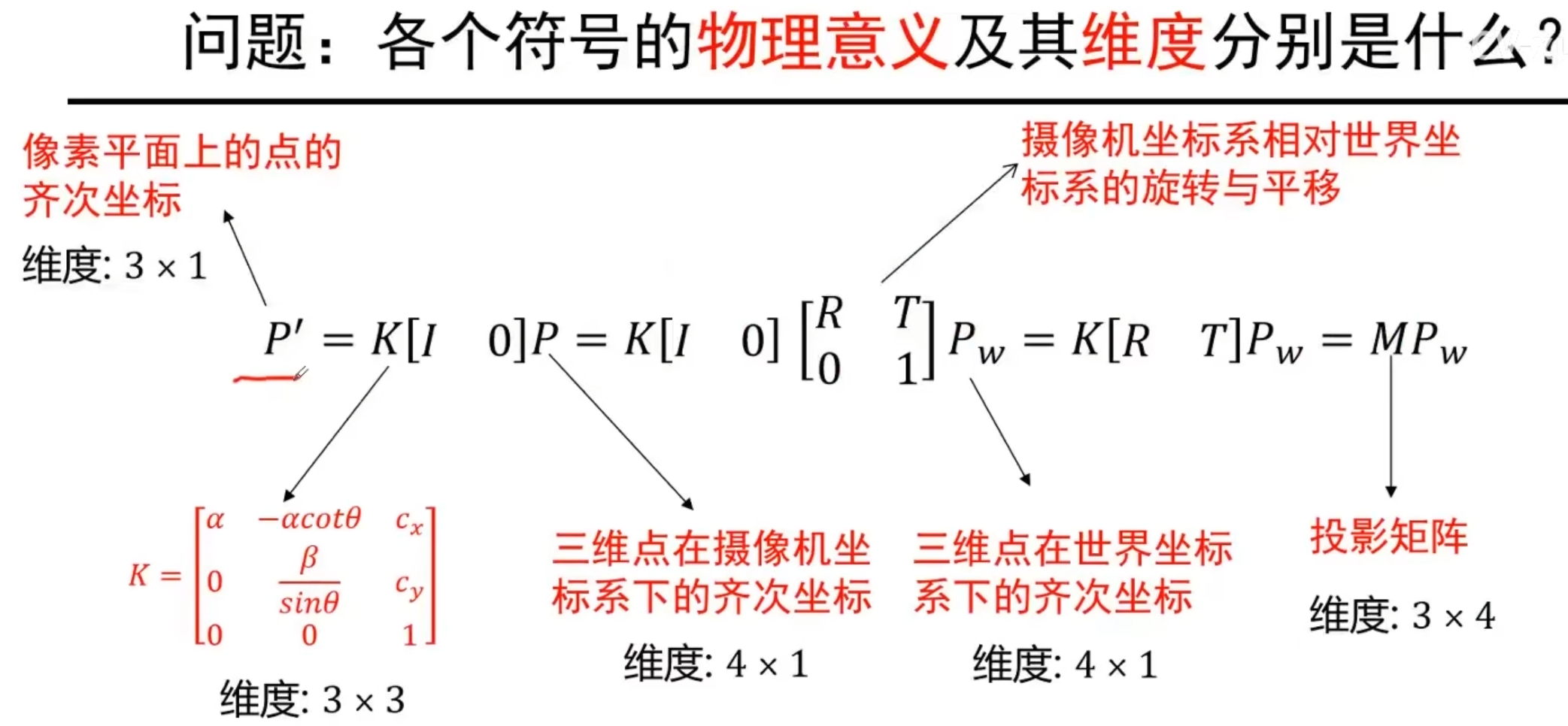
其中,R旋转矩阵关于x,y,z轴有三个旋转角度。T平移矩阵有x,y,z三个平移变量。K内参数矩阵有5个变量
所以投影矩阵一共有11个自由度
Faugeras定理——摄像机标定中证明

其中a1,a2,a3都是列向量(方便后续计算操作)
即:
a2,a3同理
零倾斜透视投影矩阵:
零倾斜矩阵且宽高比为1:
透视投影变换的性质
1.点投影为点
2.线投影为线
3.近大远小
4.角度不再保持
5.平行线相交(交点称为影消点)
其他摄像机模型
弱透视投影摄像机
当被摄物体上的各个点与被摄物体所组成的大致所在平面的相对深度远小于大致所在平面与摄像机的距离时,我们可以认为,各个点都在相对于摄像机同一个深度的平面上(比如远远地拍摄一个人的正脸,可以近似认为人身上的所有位置都距离摄像机相同的深度!)
忽略物体上各点的深度
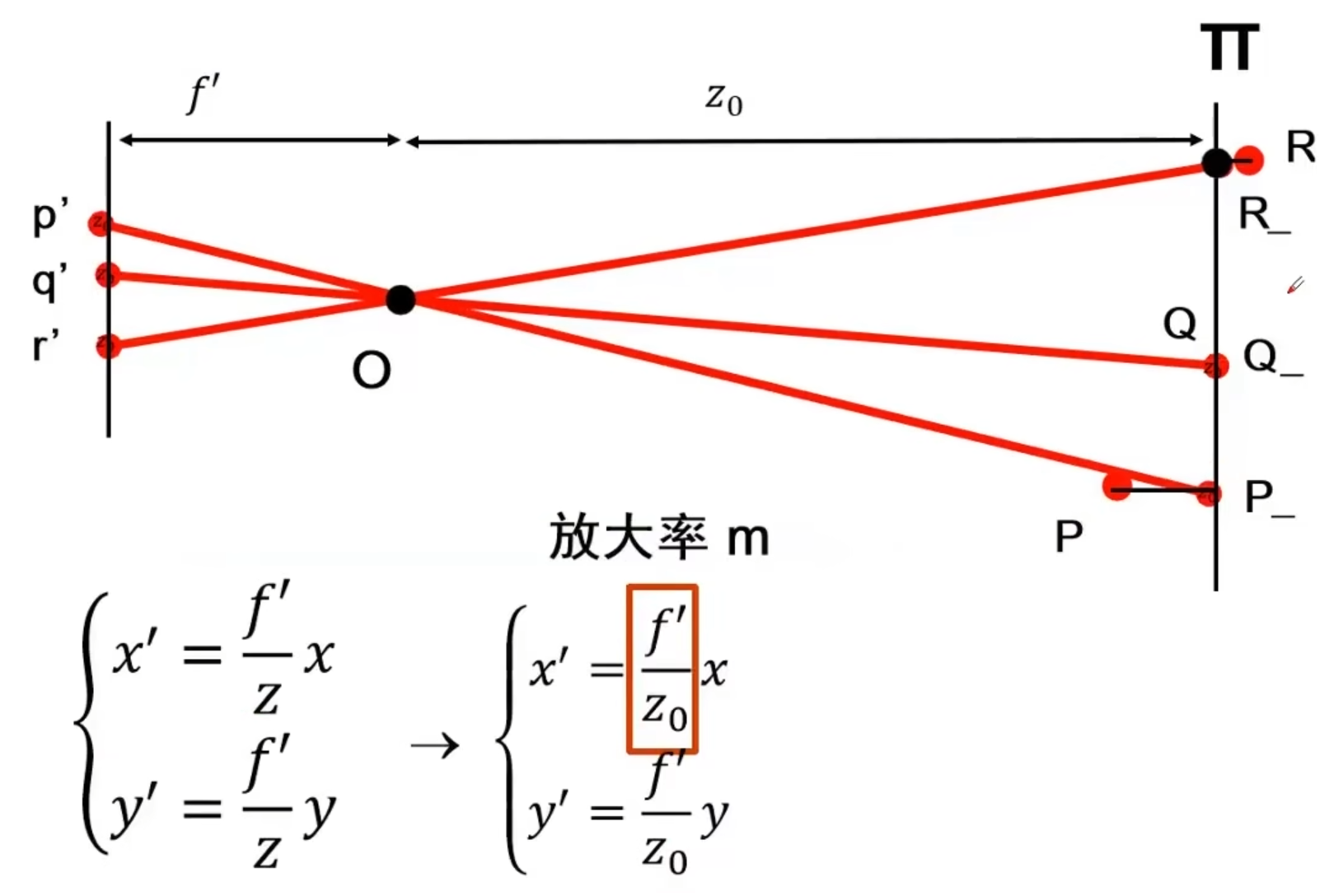
如图,P点本来距离摄像机近一些,但是我们近似为也在平面PI上
因此x^'^和x的投影映射就变成了一个线性变换(原先由于系数是f/z并不是一个线性变换)
写出该摄像机的投影矩阵,会发现v = 0,也就是投影矩阵最后一行为 0 0 0 1(课程中直接给出结论)
也就是说,弱透视摄像机的投影矩阵只有A,b,一共8个自由度,相比原来的少了3个变量
正交投影摄像机
假定相机距离物体无限远,所以所有物体都在同一个深度上。
三种摄像机的总结
正交投影:应用在AUTOCAD这种建筑设计或者工业设计的单视图中
弱透视投影:当物体较小且较远时准确,常用于图像识别任务
透视投影:对于3D到2D映射的准确建模,常用于运动恢复结构或SLAM
最小二乘解
线性方程组的最小二乘解

这里有q个未知数,p个等式
所以可知当p = q时唯一解,
p > q时:
如果 y 在 A 的列向量张成的空间内(即 y 可以由 A 的列向量线性表示),则有解(即多出来的等式实际上是已有等式的线性组合得到)
如果 y 不在 A 的列空间中,则 无解。
若无解,我们希望得到一个近似解x,使得Ax = y近似成立,作为其解
因此使用最小二乘法
即得到一个x,使得
求解方式:

齐次线性方程组的最小二乘解
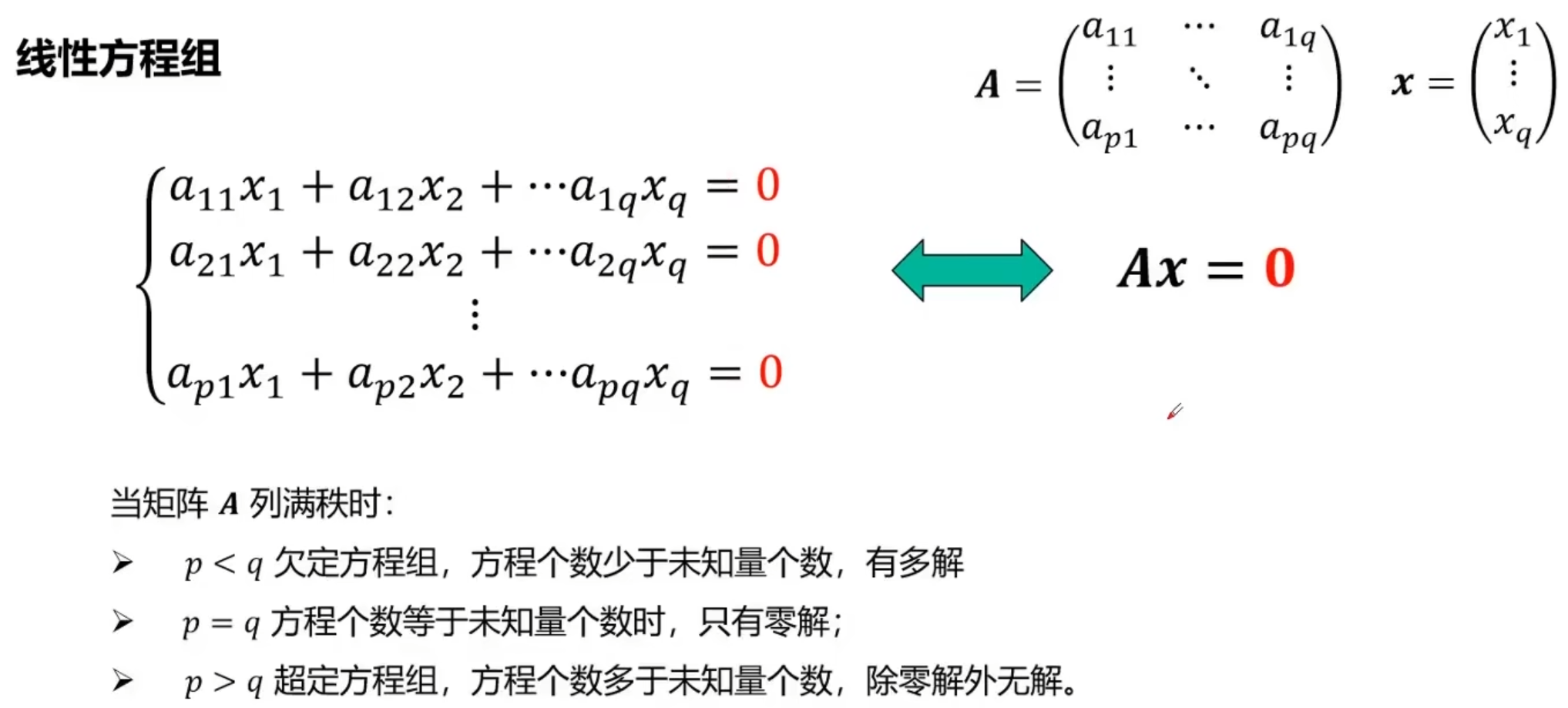

为什么要让x的模为1?
因为如果不做约束,Ax的模可以无限放大,因为Ax=0,则Aλx=0也是其解,所以要约束
非线性方程组的最小二乘解

2.摄像机标定
摄像机标定:即求解摄像机的内,外参数矩阵
符号说明
以后像素平面的点用小写p表示,世界空间的点用大小P表示
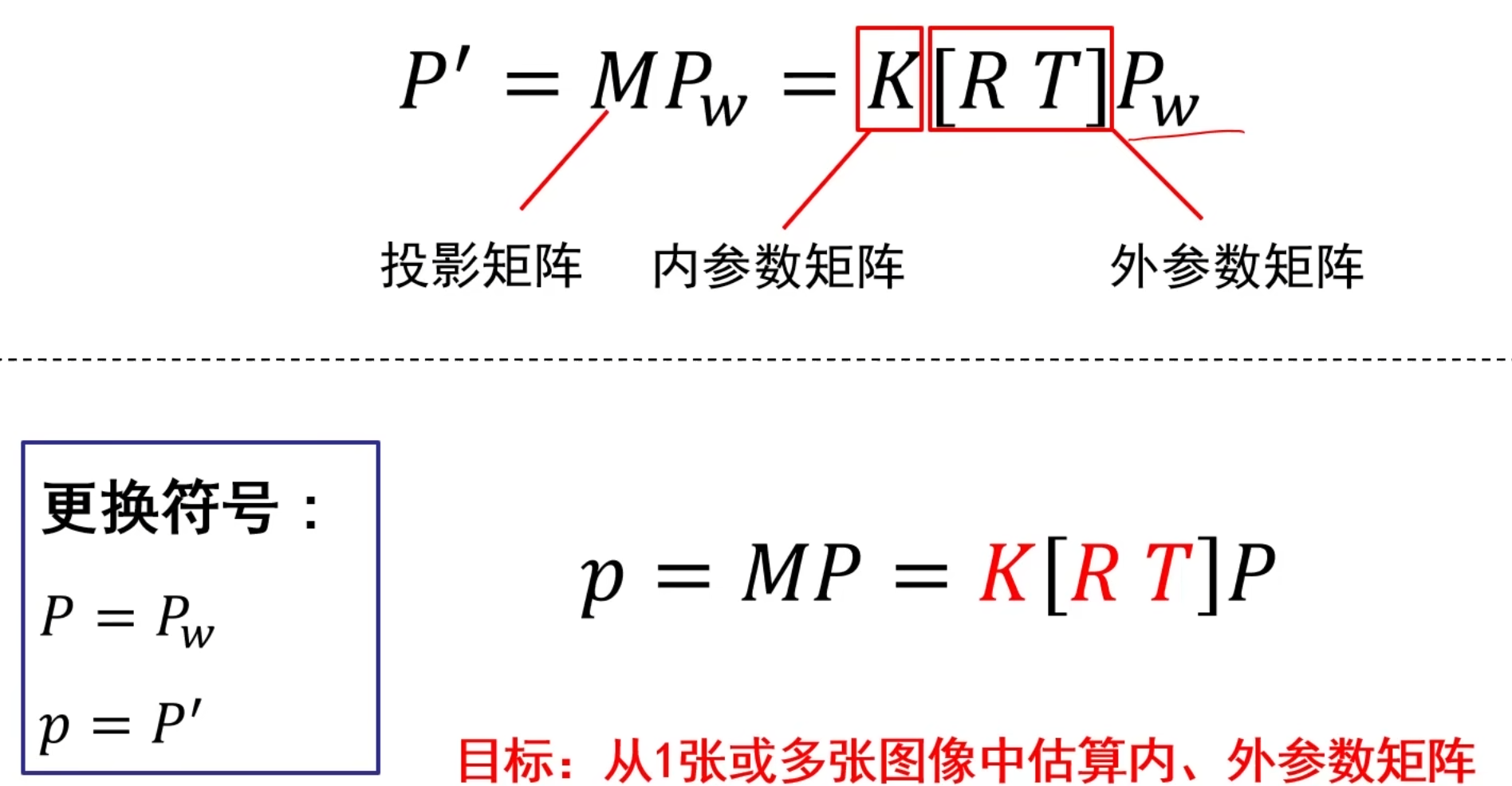
求解投影矩阵M
已知像素平面坐标和世界空间下坐标,求解投影矩阵M中的内外参数矩阵的过程就是标定
我们先求解投影矩阵M
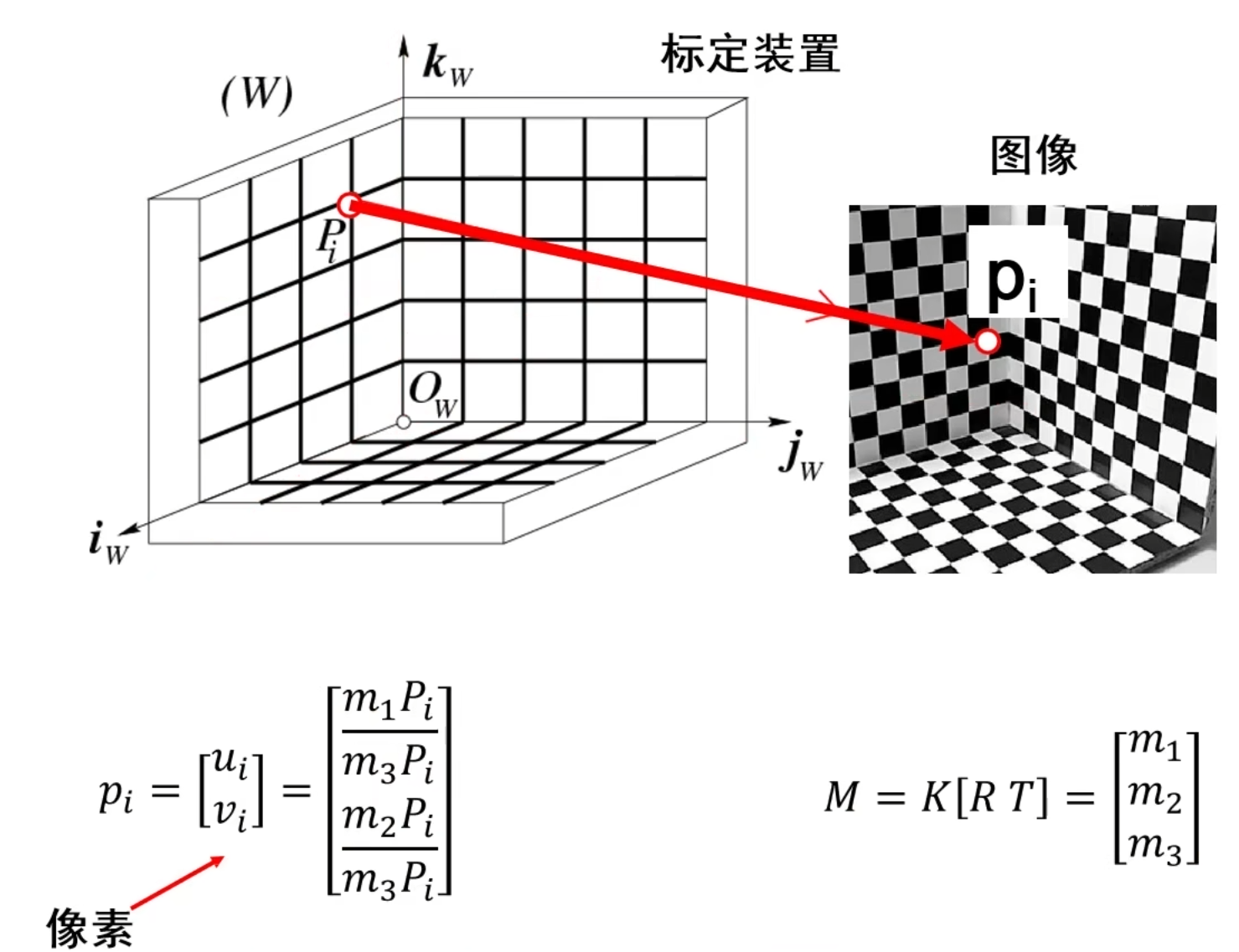
把M矩阵写成m1,m2,m3行向量组成的矩阵(每一个m是一个1x4行向量),再把齐次坐标除以最后分量得到欧氏空间坐标
可以得到左边的等式。
左边等式中
我们知道M矩阵有11个自由度, 通过上面的等式整理可得下图:
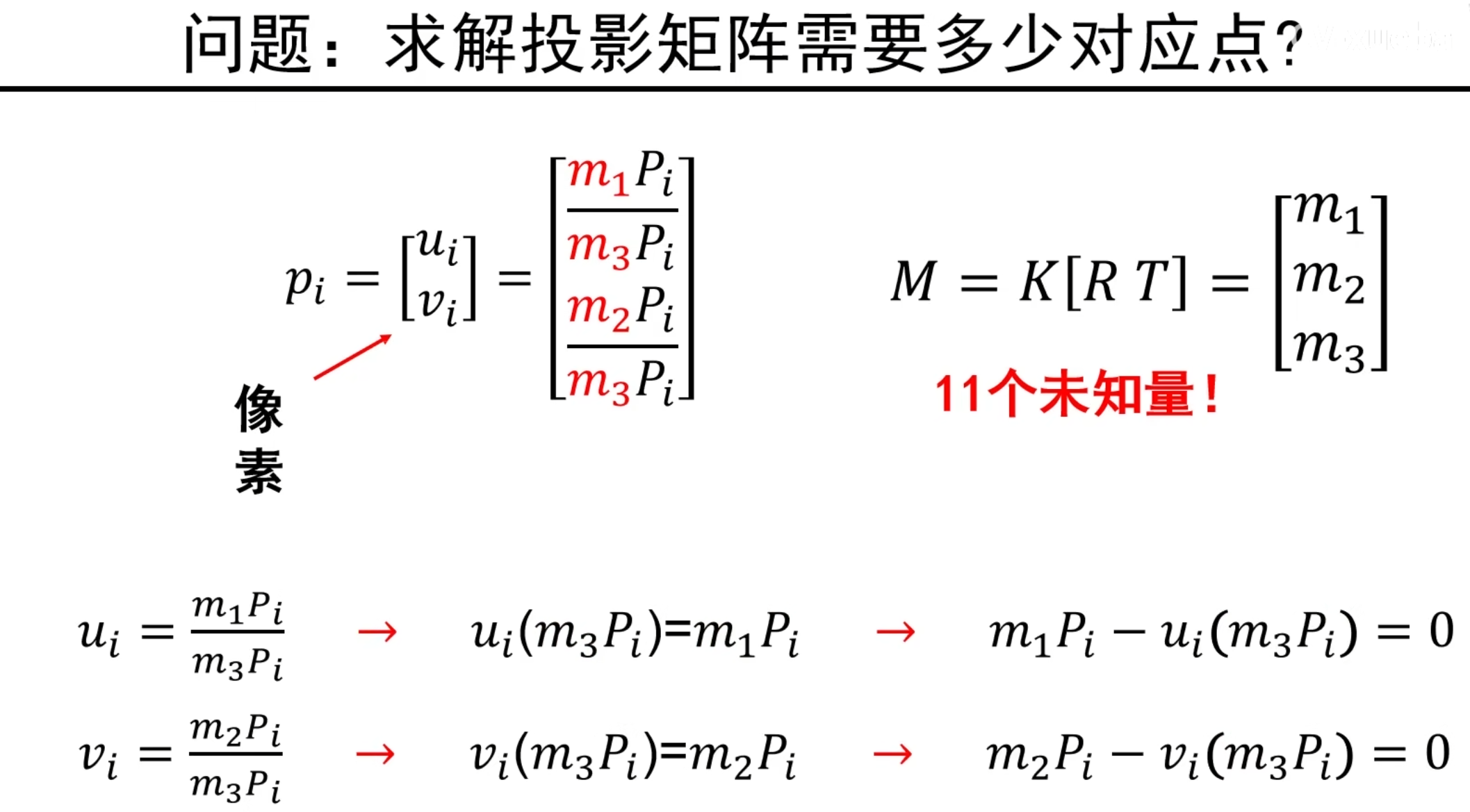
可见,一个点坐标(像素空间+世界空间),可以得到两个方程
所以我们最少需要6个点,才能解得M矩阵,但实际上需要使用多于6个点来得到更鲁棒的结果
再进一步进行构造整理:

我们可以把n个点提供的2n个方程组改写整理成Pm = 0的形式,其中P是我们为了构造Pm=0构造出来的矩阵
可见,该问题转化为了求解一个超定齐次线性方程组的解的问题!使用上节课的最小二乘法来做!

A是3x3矩阵,b是3x1列向量
如此便可以通过最小二乘法解得近似的投影矩阵M,这个M和我们实际的标定矩阵M会相差一个比例系数(因为是通过最小二乘得到的)
求解内,外参数矩阵
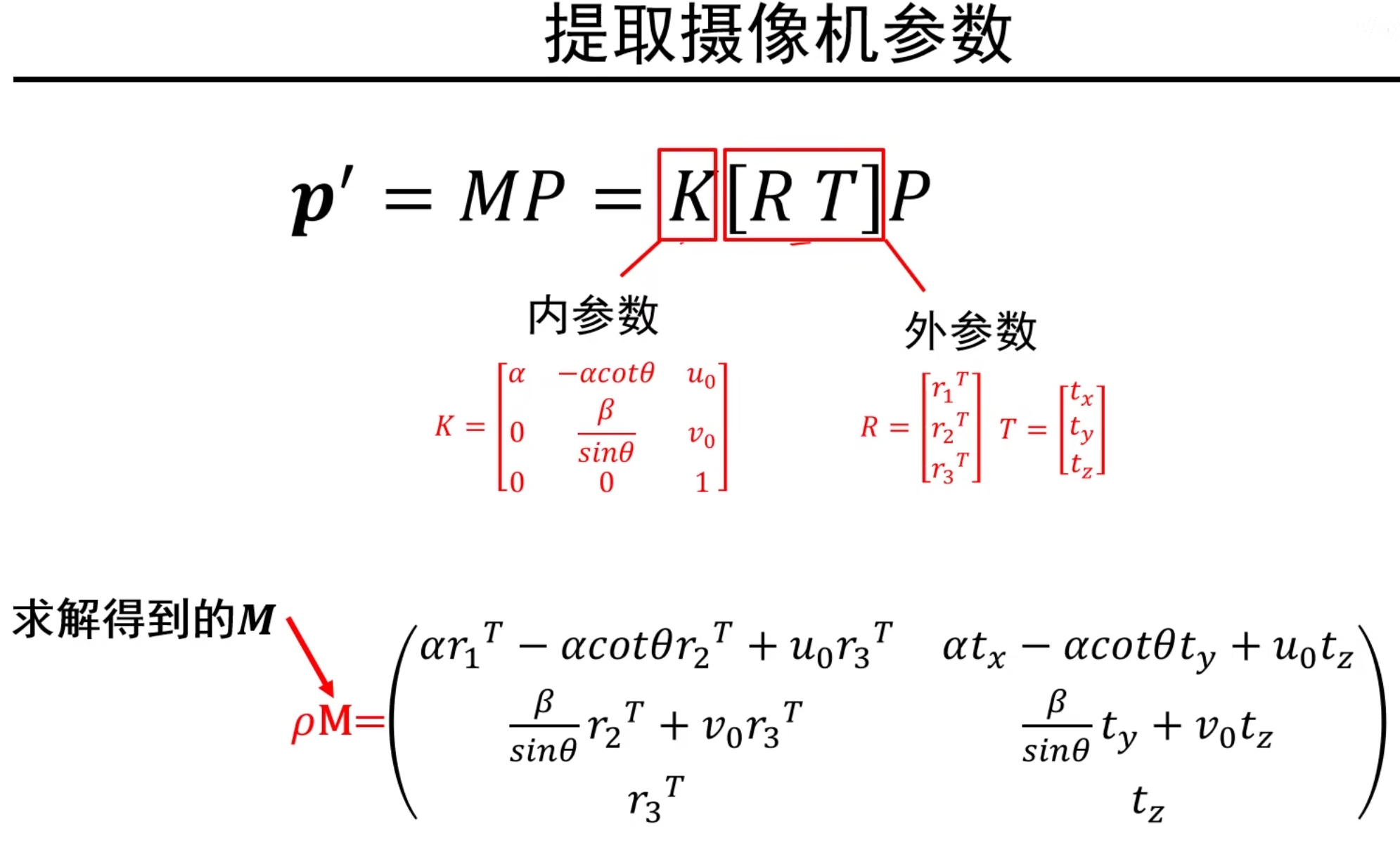
注意:r1是一个列向量,所以r^T^就是一个行向量
正交阵定义:设A是一个方阵。若A^T^A=I或AA^T^=I,则A为正交阵
同时,我们知道旋转矩阵和逆变换相乘等于不变,也就是I,而且易得旋转矩阵的逆就是其转置,故旋转矩阵是正交阵,因此r1点乘r2为0,r1叉乘r2为r3同向的向量,且根据旋转矩阵的公式,我们知道r1,r2,r3的模都为1!
通过代入K,R,T未知量,得到了最下面的右边的一堆东西,这一堆东西表示标定的真实的矩阵,所以左边用ρM表示我们计算的M和真实的M差了一个比例系数ρ
现在先求解u0和v0——即cx和cy,代表成像平面到像素平面的位移偏移量
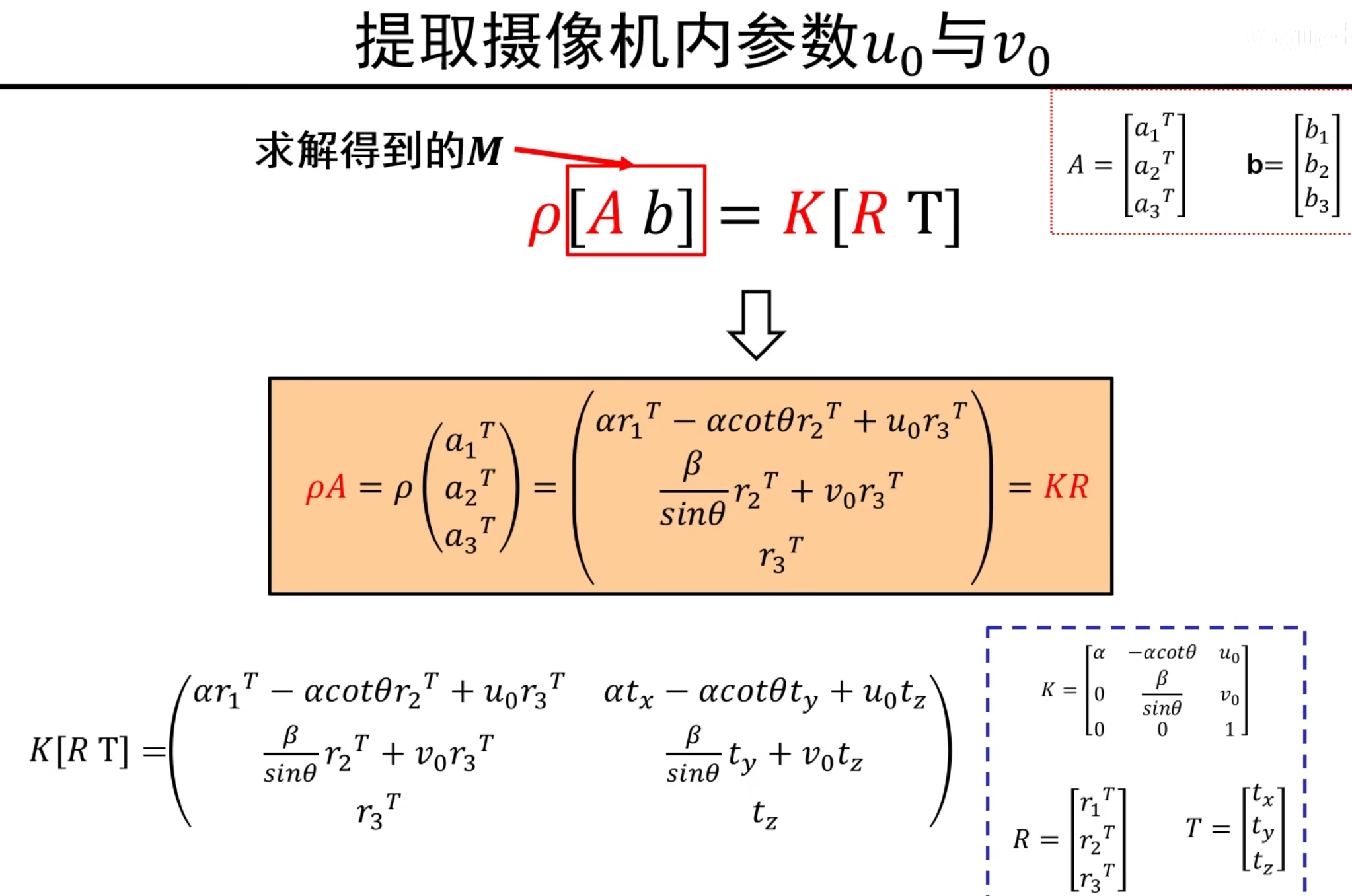
我们已知通过最小二乘已经解得了[A b],通过分析也可知K[R T]带未知数的形式
因此进行等式联立,如上图
求解ρ
求解u0,v0(cx,cy)

求解θ
经过下图化简:使用红框的方法求上面面红色部分的模(即向量的模=向量x向量的转置),得到右边
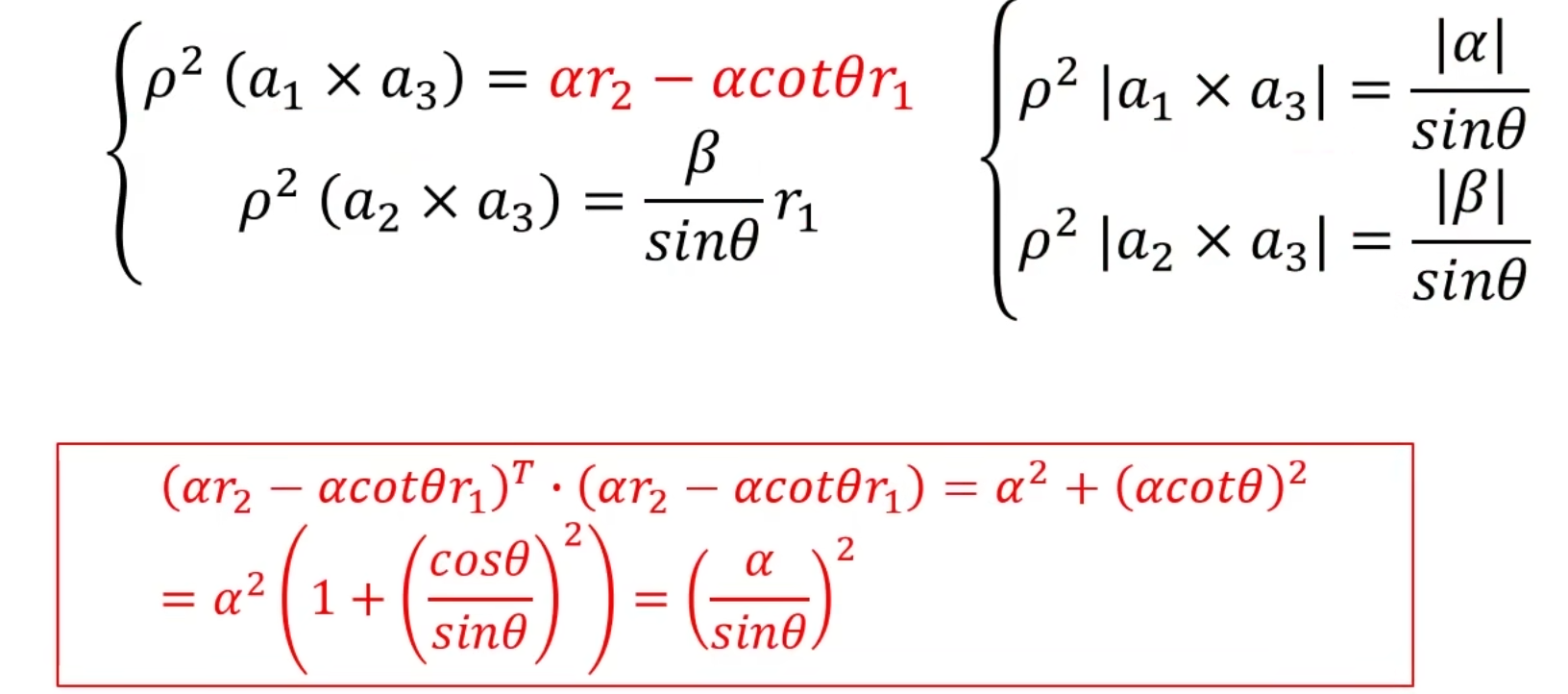
继续求解cosθ

观察cosθ的等式,可以发现,如果cosθ为0,则要求(a1xa3)(a2xa3)=0
回顾上一节的Faugeras定理

我们就此推出该公式里面像素是一个矩形的条件!
求解α,β
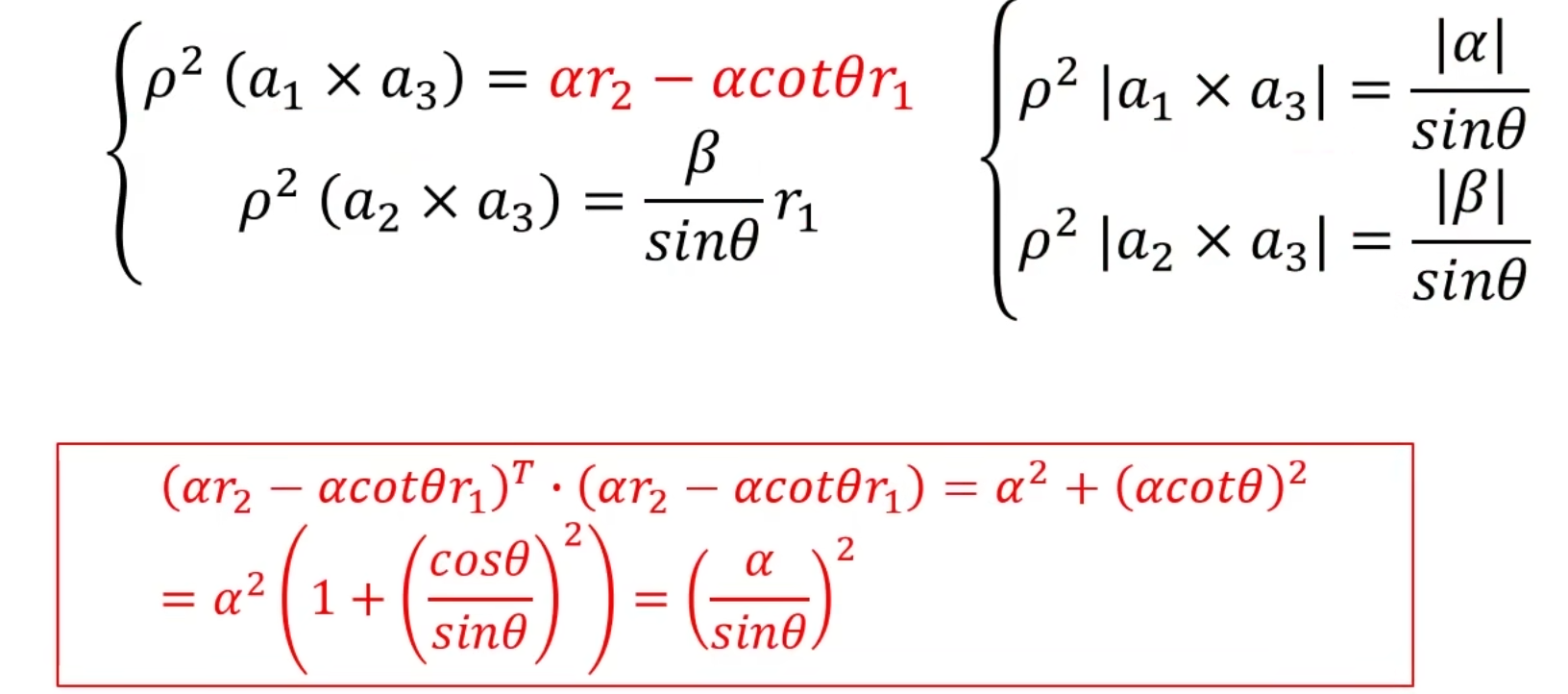
还是该结论,我们把右边的α和β放在一边就可以求得
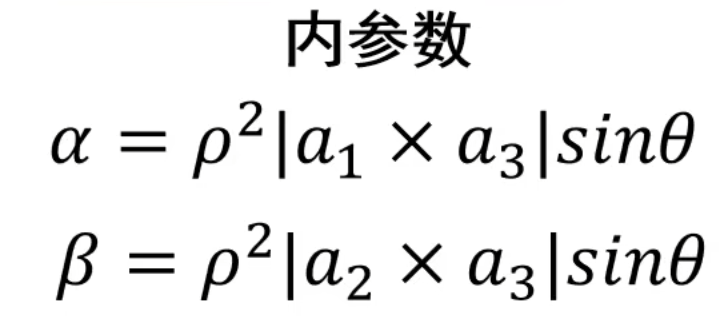
我们又推出了Faugeras定理的其中一条!像素为方形的(宽高比为1)

求解外参数r1,r2,r3

r~3~可以立马得到,因为r3 = ρa~3~,代入ρ可得
r~1~=ρa~3~ x ρa~2~
r~2~=r~3~ x r~1~
求解外参数T
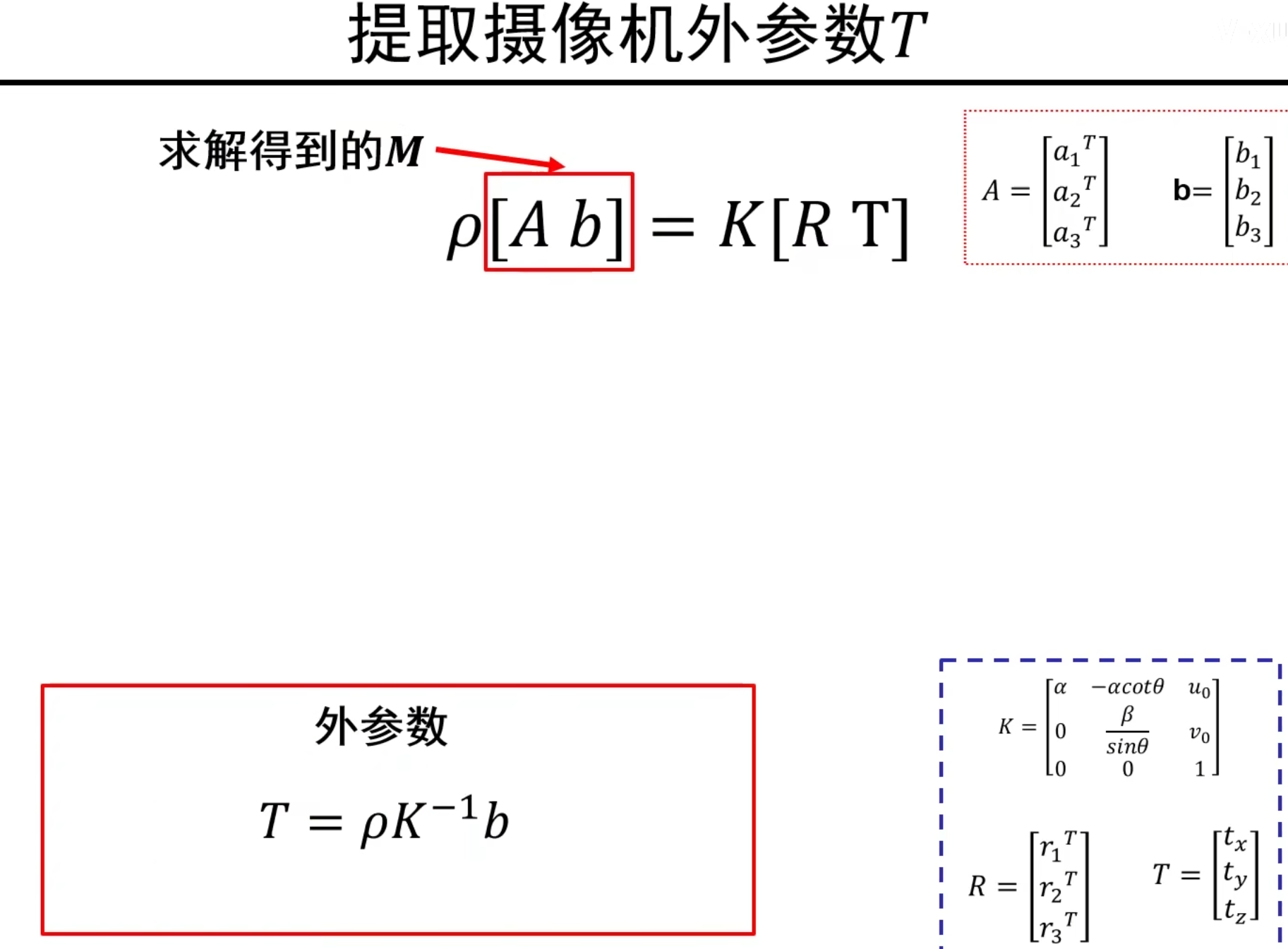
摄像机参数求解总结
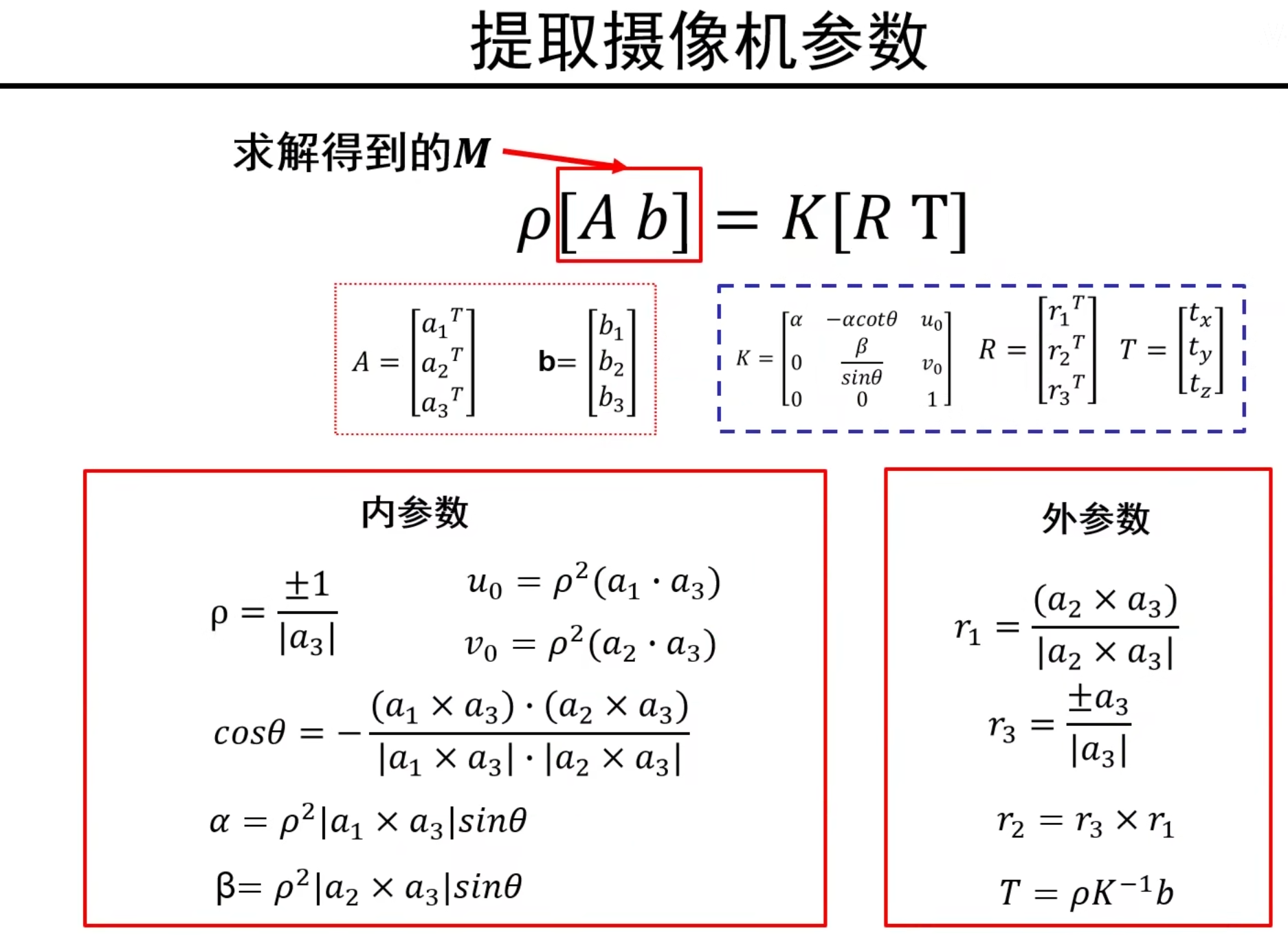
取P点的说明
取的六个点不能全部位于同一平面!因为同一平面会有相关性,会退化
径向畸变的摄像机标定
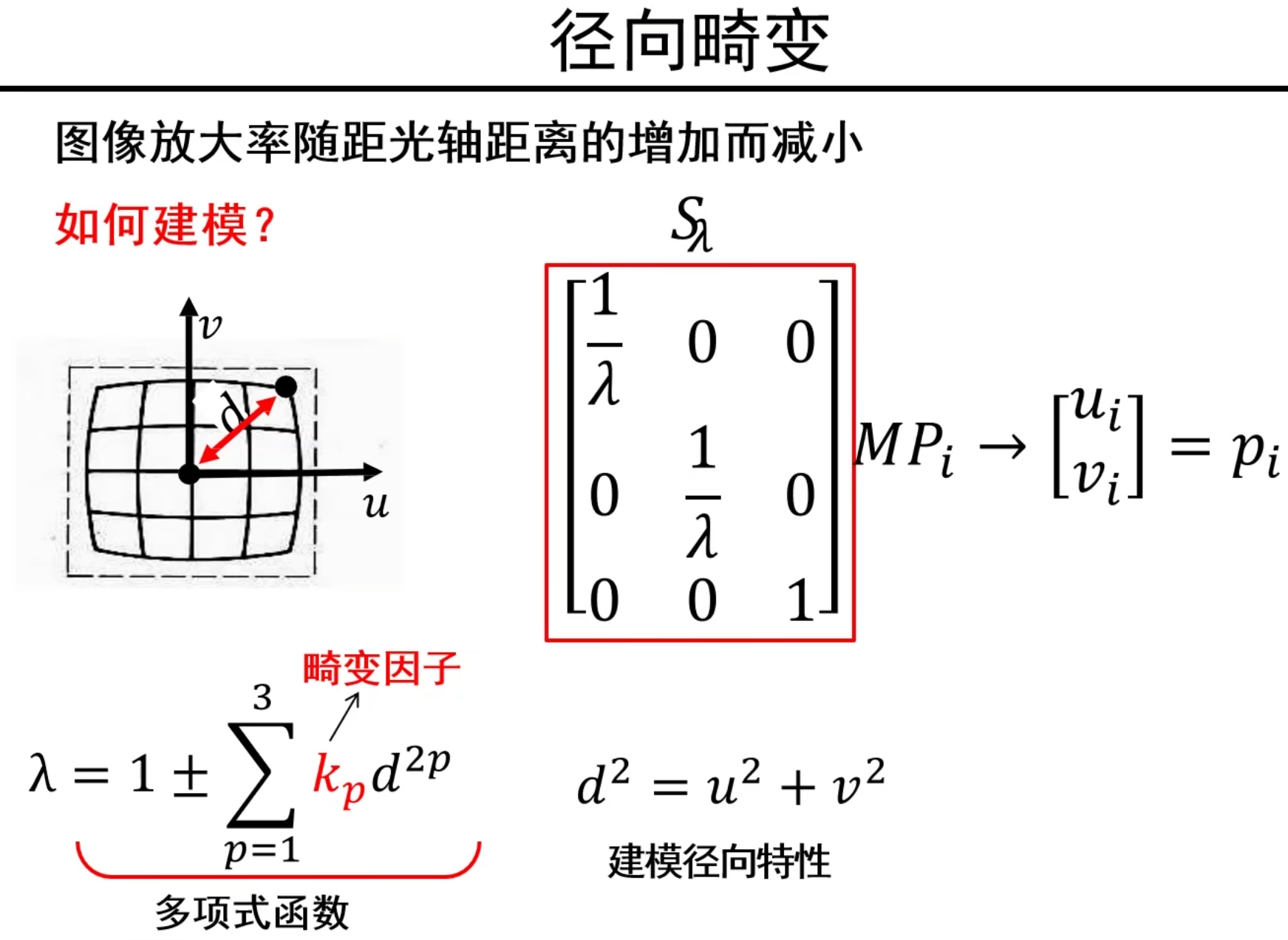
P~i~是一个世界空间的点,经过MP~i~得到的是无畸变相机的像素空间下坐标。
经过**S~λ~**的缩放变换,就得到了畸变的坐标!
K~p~是一个系数
其中,λ的值由底下的多项式决定。d是MP~i~,也就是在无畸变相机的像素空间下坐标距离图像中心的距离的平方
可见,d越大,如果λ是+,1/λ就越小,也就是径向向里收缩,对应桶形畸变。如果是-号,对应枕形畸变。极端情况下,在原点处没有畸变,也就体现了镜头中越靠镜头外畸变越明显
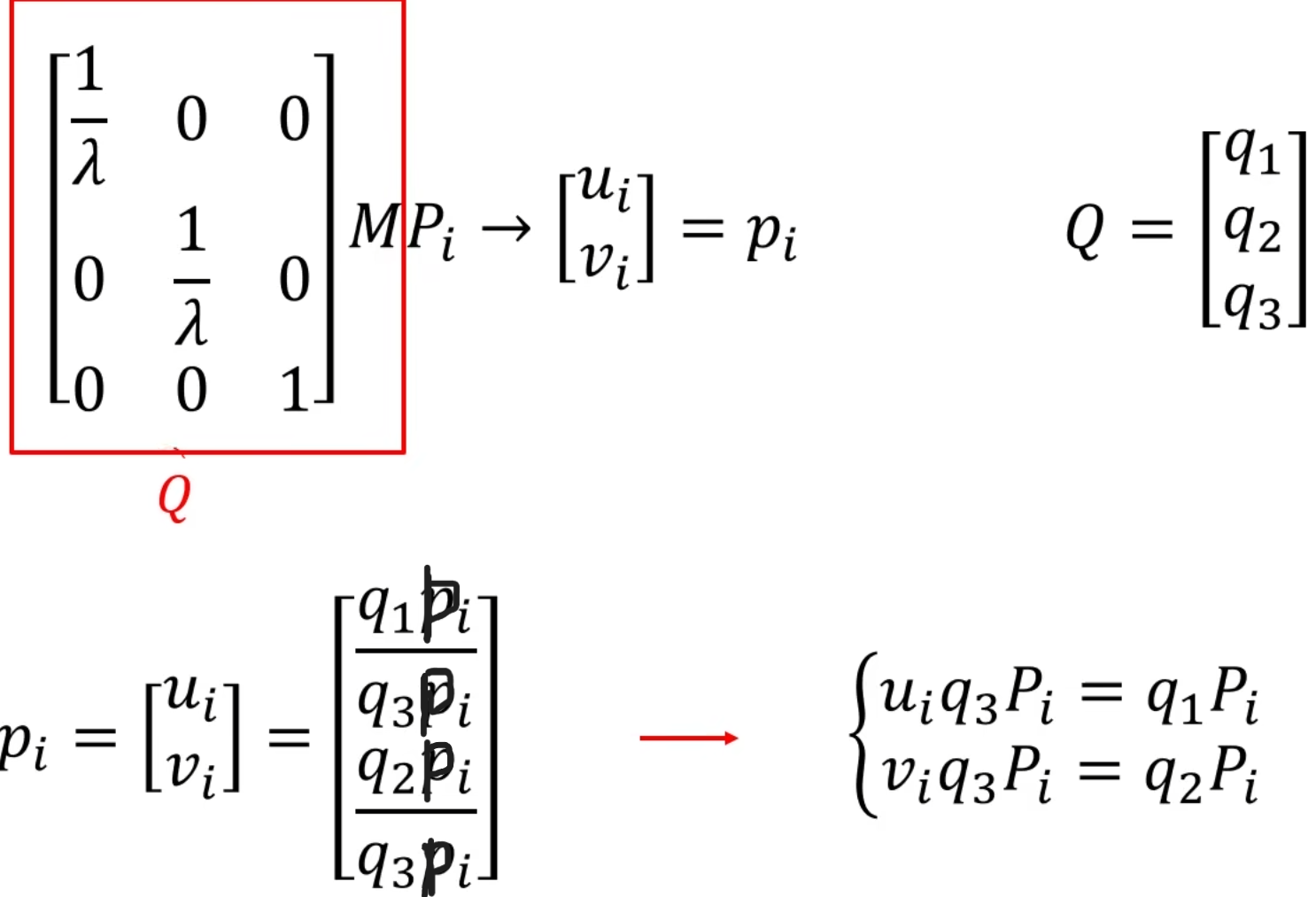
我们把畸变缩放和无畸变投影矩阵合成一个变换矩阵Q
如上图进行整理(还记得吗,p~i~小写,是像素空间的点坐标)

回想我们在做理想摄像机标定的时候,这这一步写成了Pm = 0的线性齐次方程组,因为P矩阵是已知的所以为线性
但是此处,q是p和缩放矩阵的合成,而缩放矩阵的λ存在未知数,因此是非线性的!
因此,我们将使用非线性方程组的最小二乘解

具体二乘法不做推导
但是,如果初始解与实际相距较远,可能会很慢,因此我们试着先求出线性部分以找到近似解,再拿解去迭代
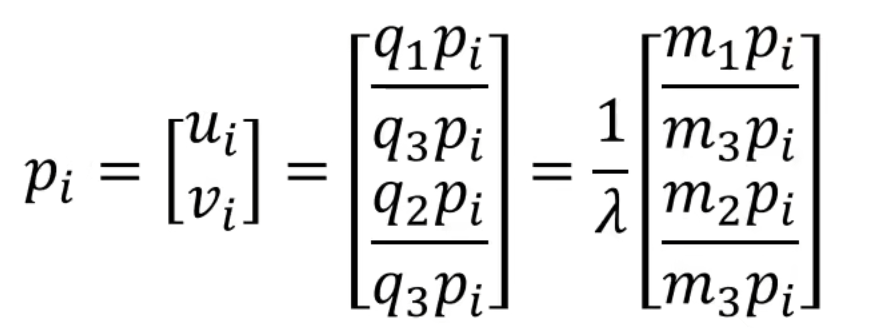
先把λ取出来,然后把u~i~/v~i~得到:

可以发现,我们把λ这个未知量约掉了,使用Ln = 0,把方程组改写成了一个齐次线性方程组,就可以使用最小二乘法的奇异值分解得到解!
这样我们搞定了部分变量,再进行迭代法可以加快求解的收敛速度
(k~1~,k~2~,k~3~是前面λ里面的畸变因子)

2D平面的变换
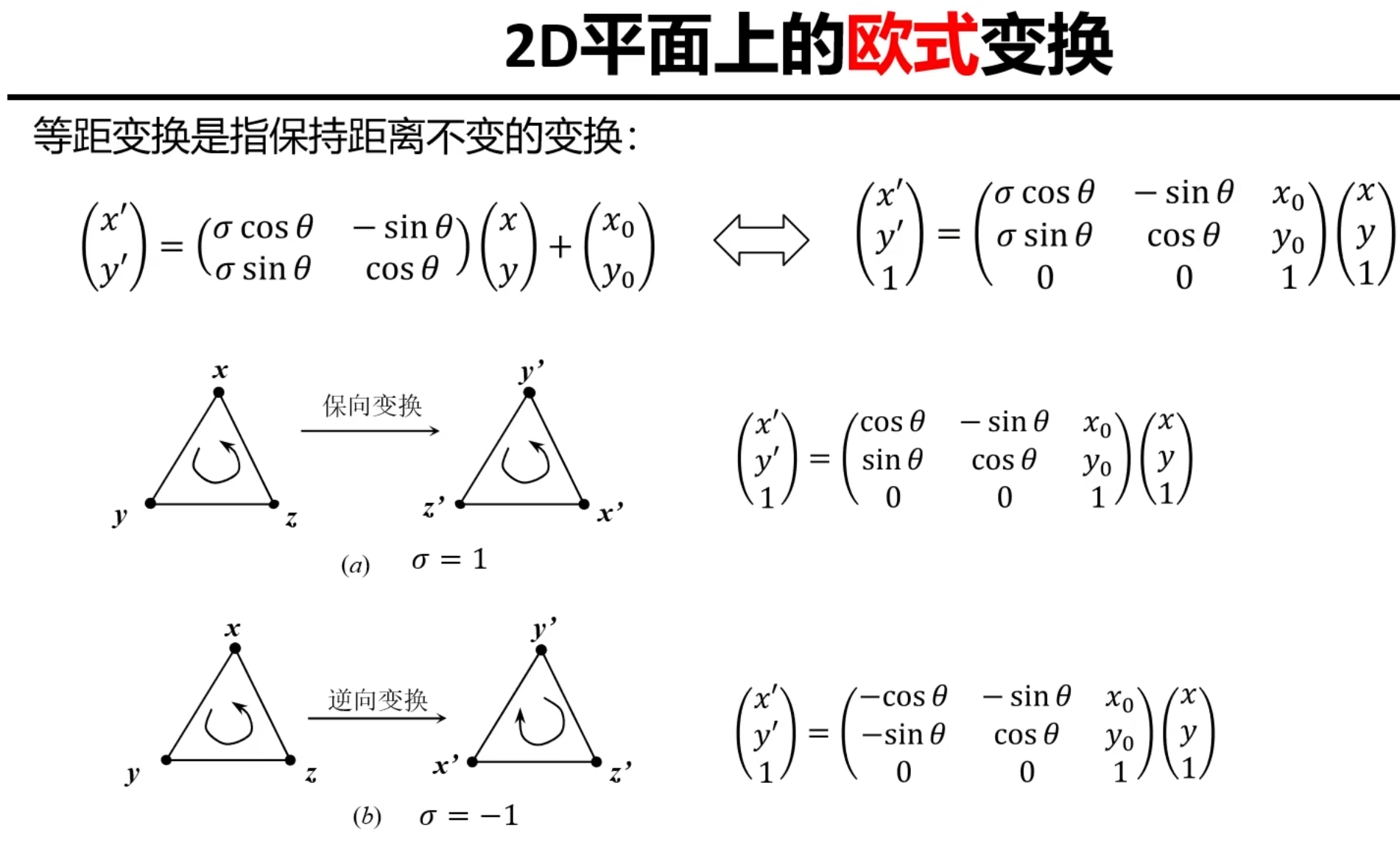
σ取1是逆时针旋转变换+平移,-1是顺时针旋转变换+平移
上面的叫等距变换,原因是变换完以后x^‘^^2^ + y^’^^2^=x^2^ + y^2^
同时,我们称σ=1的等距变换为欧式变换
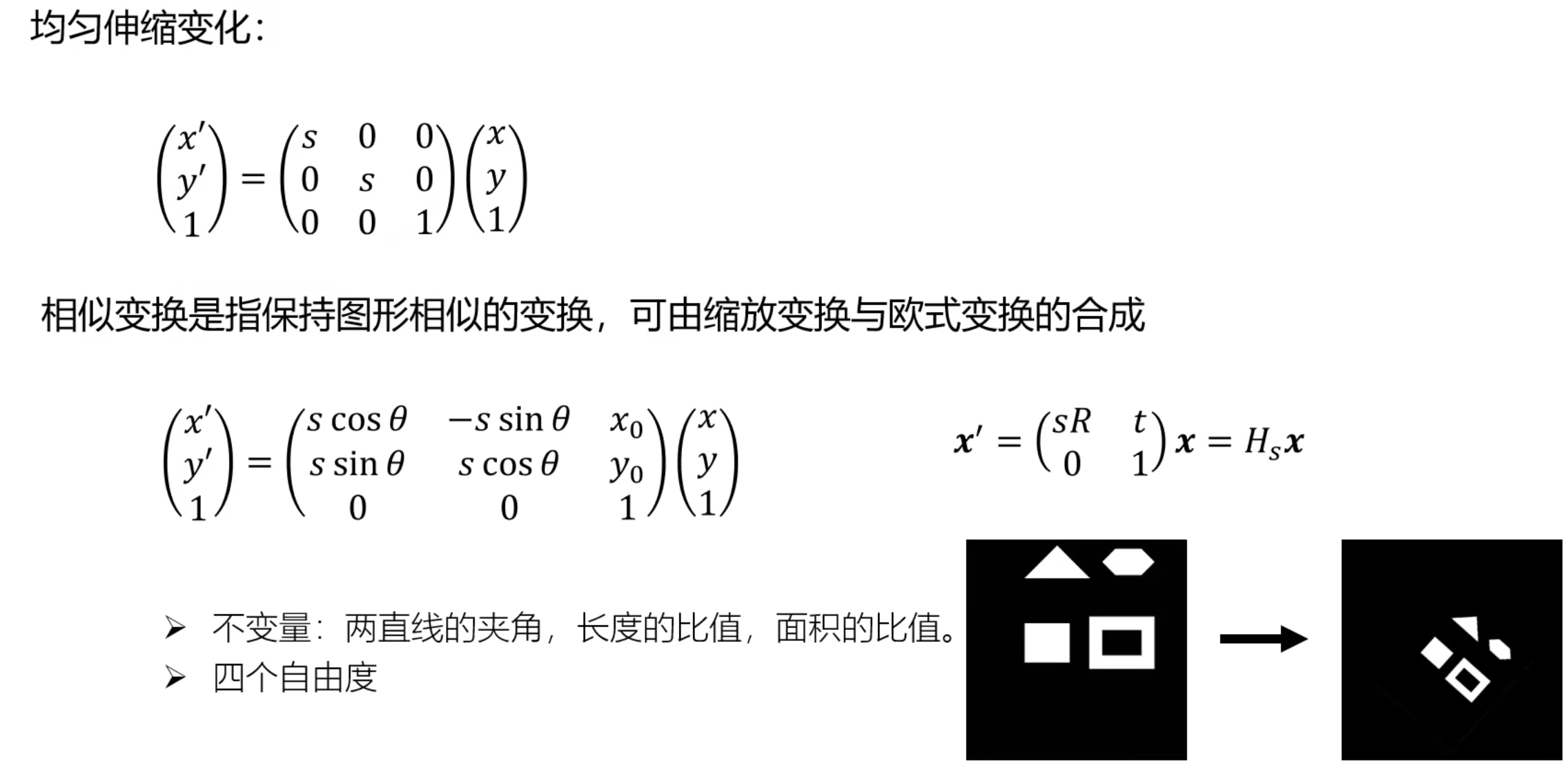
仿射变换

透视变换

3D空间的变换
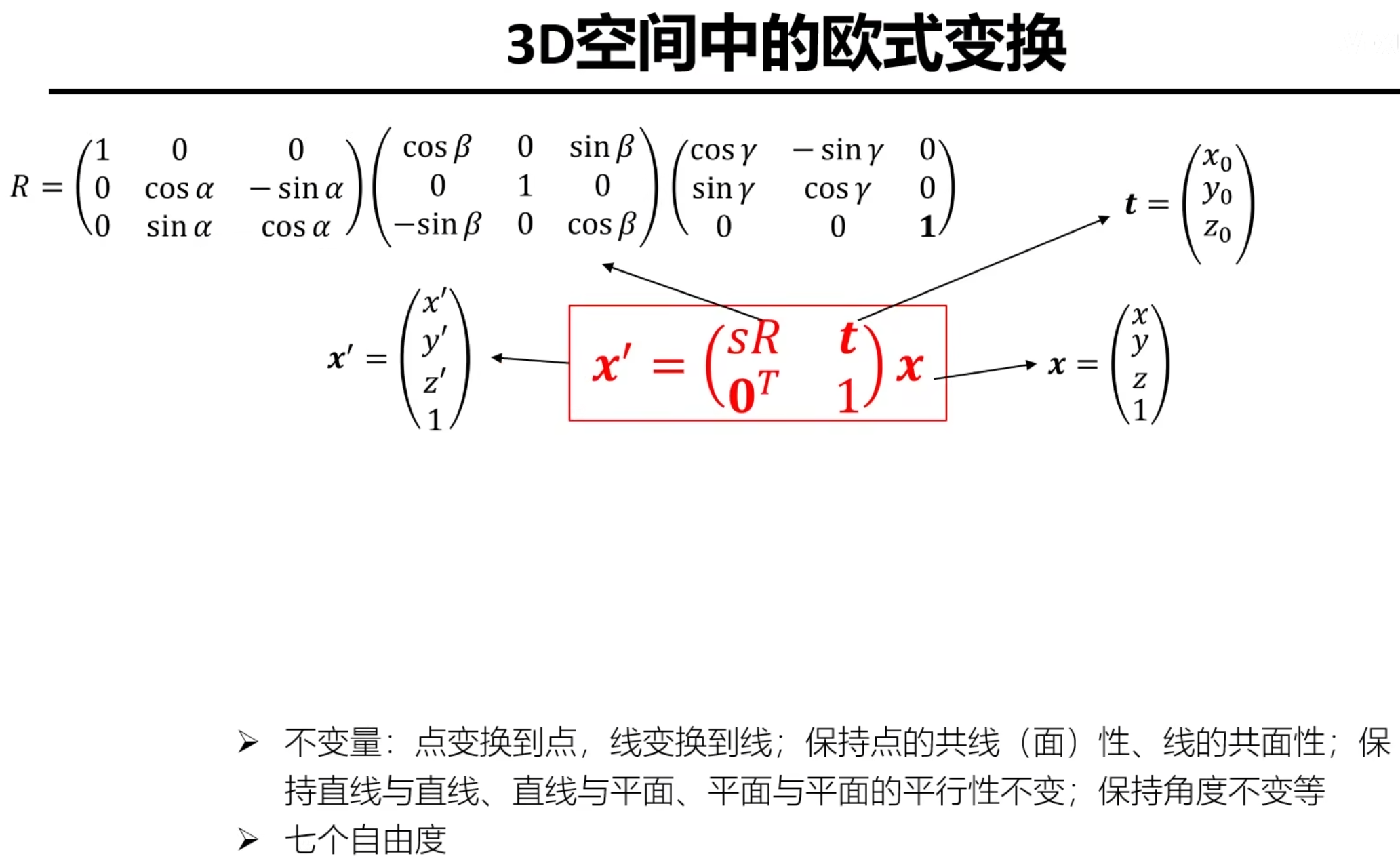
仿射变换
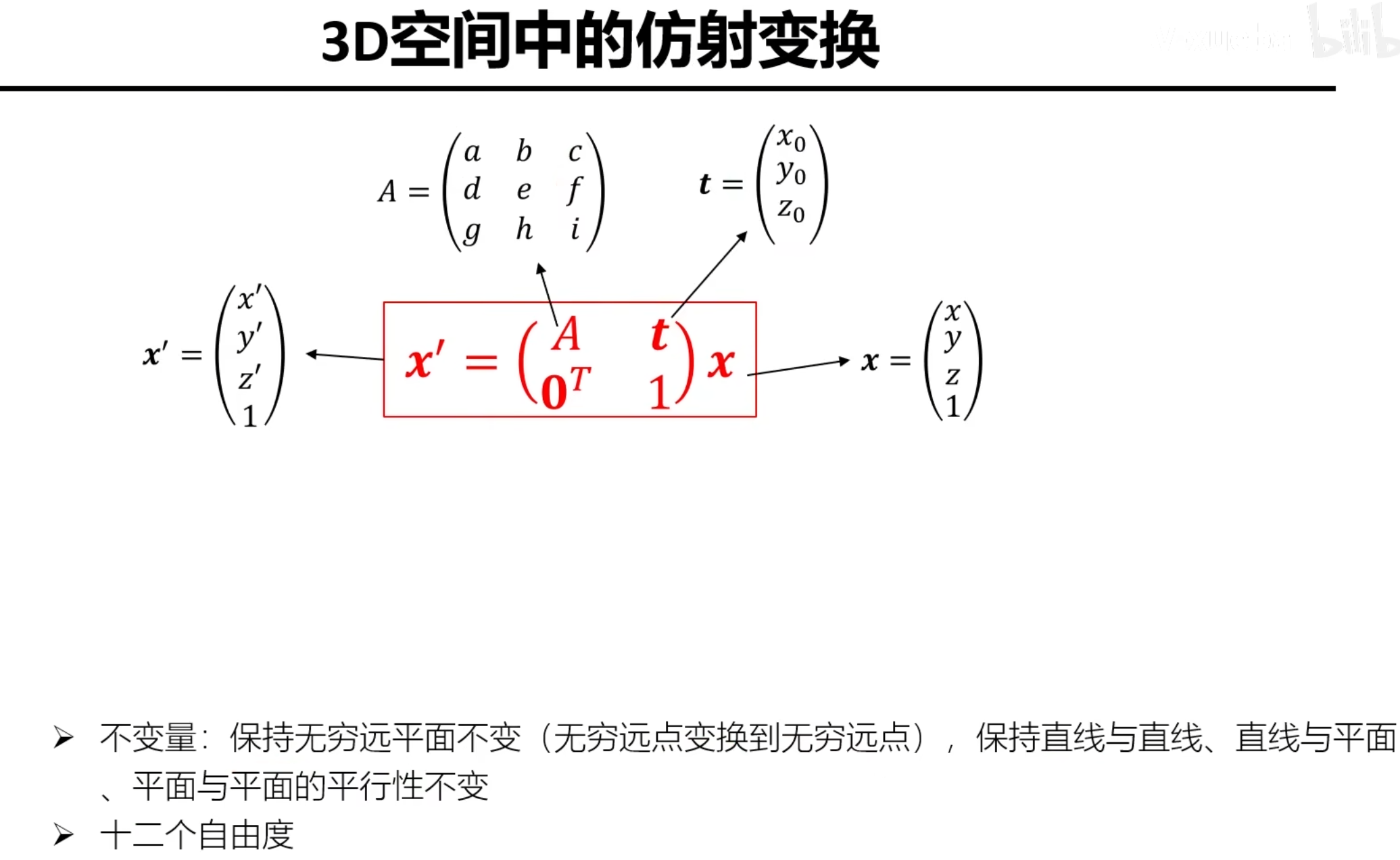
透视变换
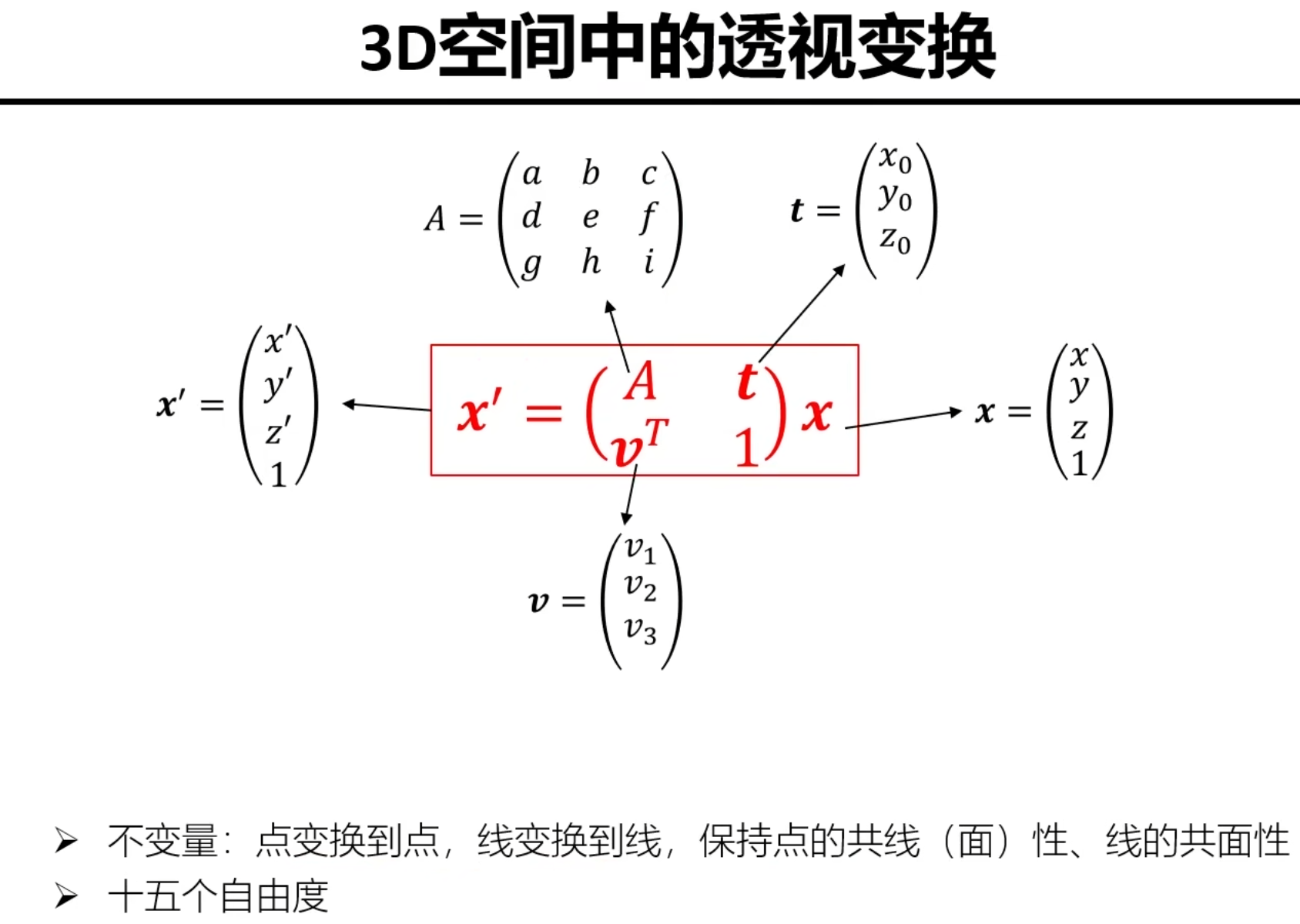
3.单视图几何
无穷远点,面,线
2D平面上的直线表示
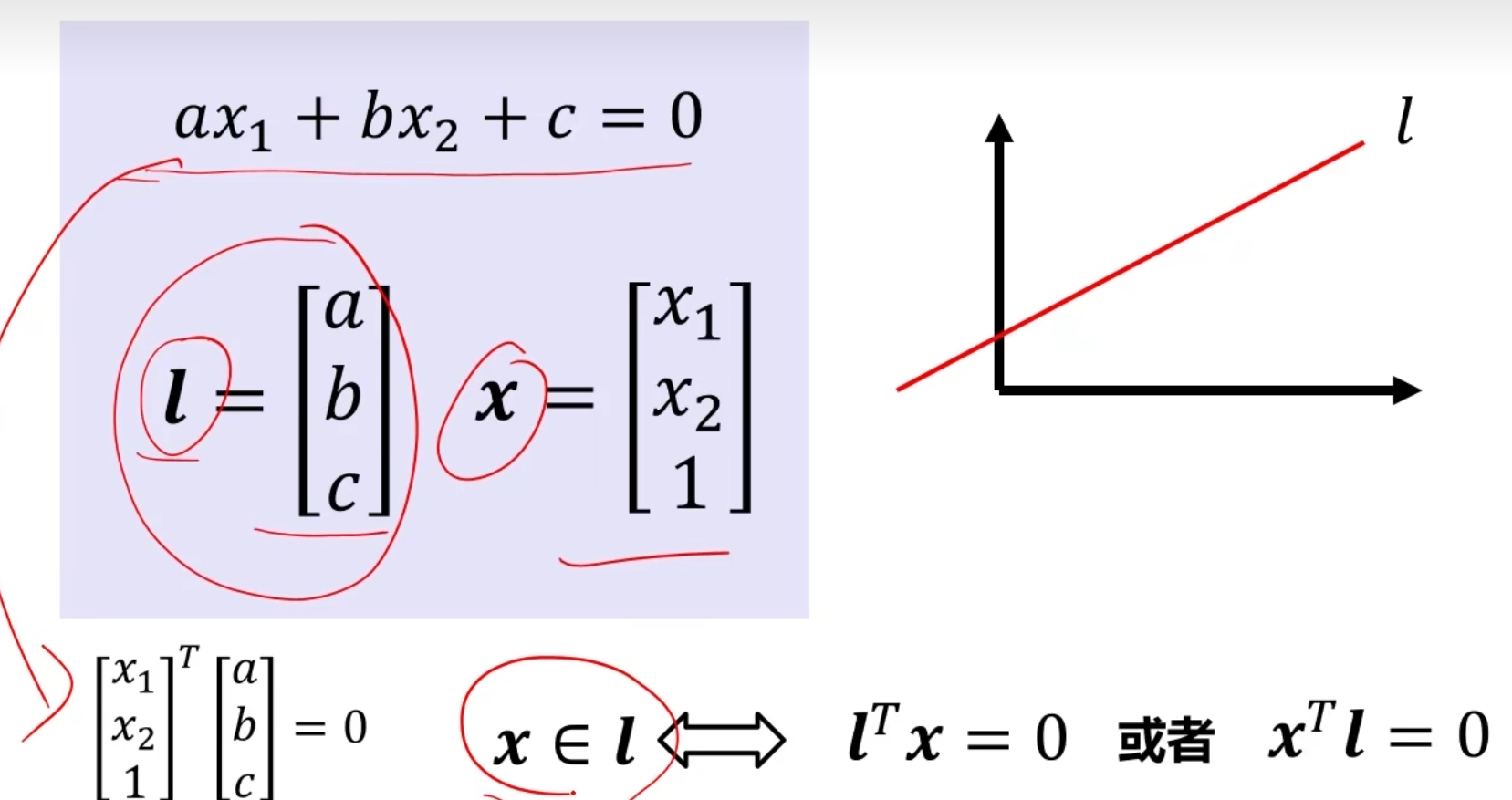
使用向量表示,方便后面计算
两条直线的交点:

这里很神奇,x其实是叉乘出来的一个向量,但是由于点乘=0,与我们上图的直线定义中直线上的点的定义重合了,所以这个向量x如果看作一个点的坐标,这个点就在l和l^'^上!因此得证
2D中无穷远点
欧氏空间中平行线的定义:
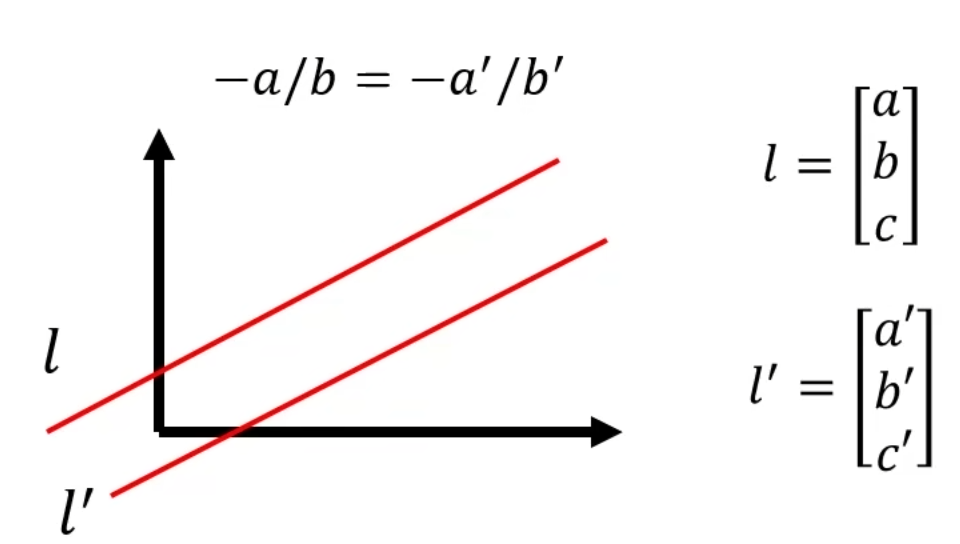
在齐次坐标下,求两个平行直线的交点,使用上面叉乘求交点的方法,可得如下:



(灰色框框是叉乘的矩阵表示形式)
可以发现,得到的交点最后一维分量为0,说明两个平行线的交点是一个无穷远点
可以继续得到小结论:
想要得到一个直线的无穷远点,就取其方向向量再加一维0即可,如l直线是[a,b,c],则其方向向量是[b,-a],法线方向是[a,b],无穷远点是[b,-a,0]
2D中无穷远线
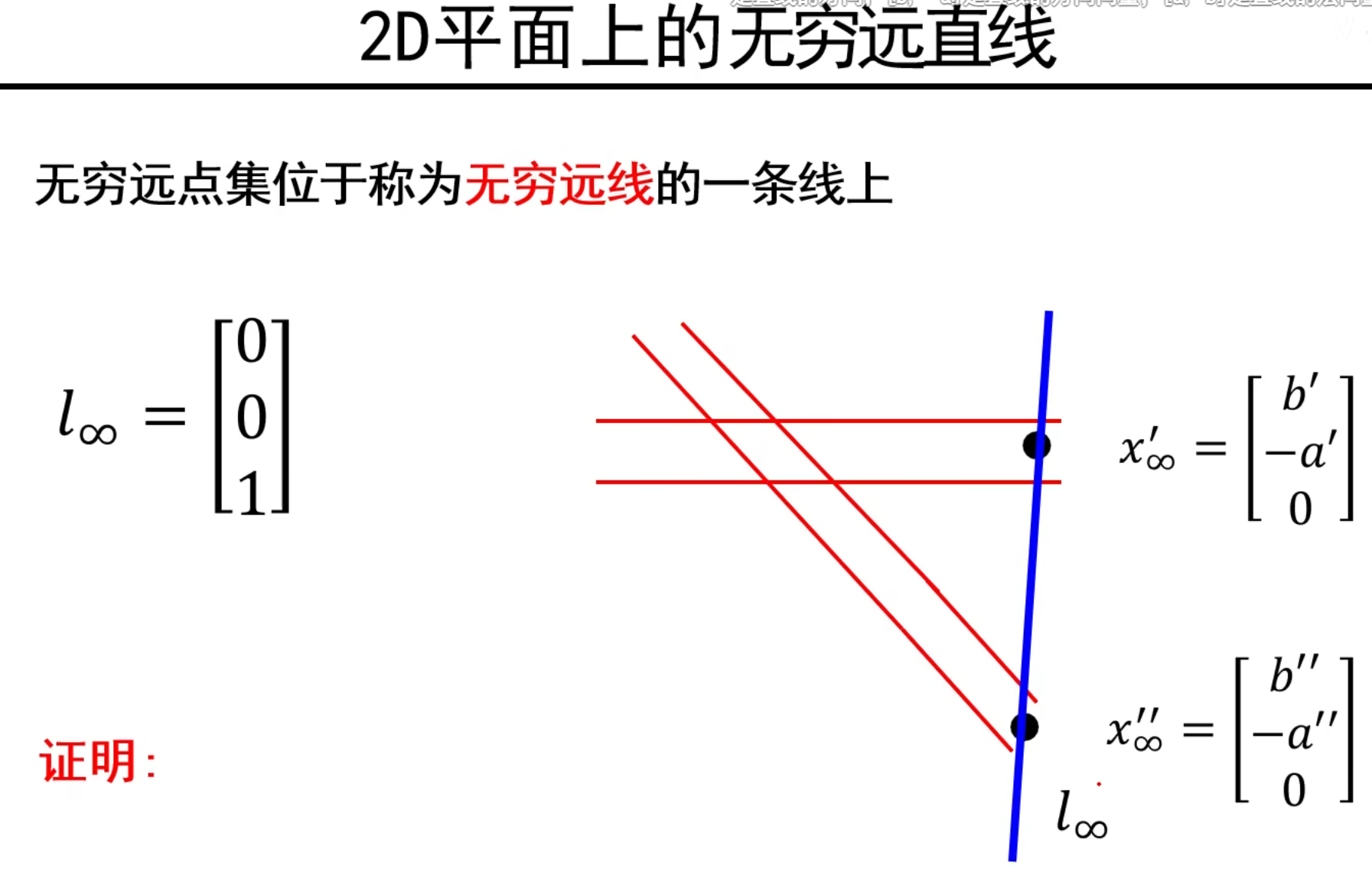

3D中的面表示
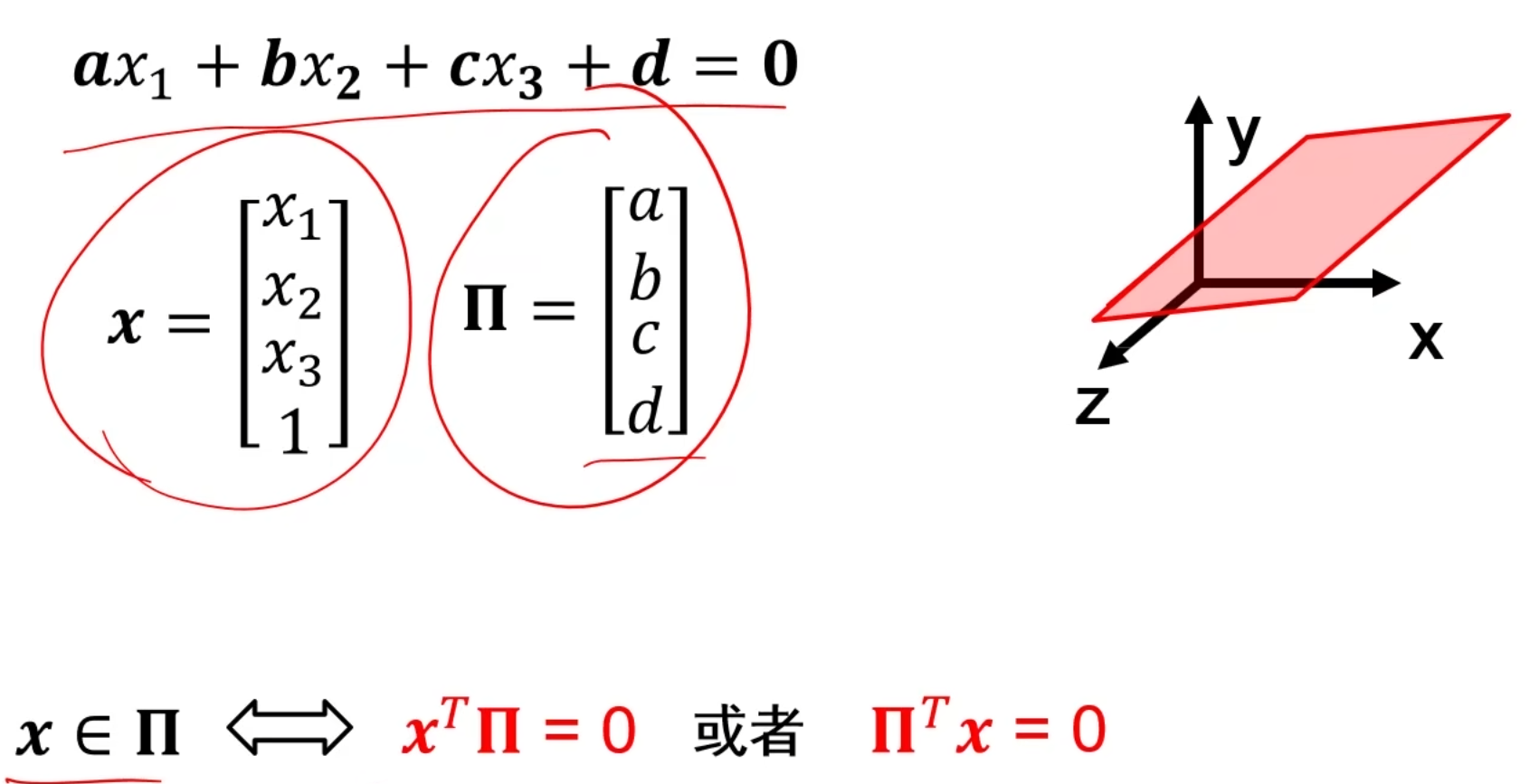
其中,n = [a,b,c] 就是平面的法向量
3D中的直线表示

3D中的无穷远点
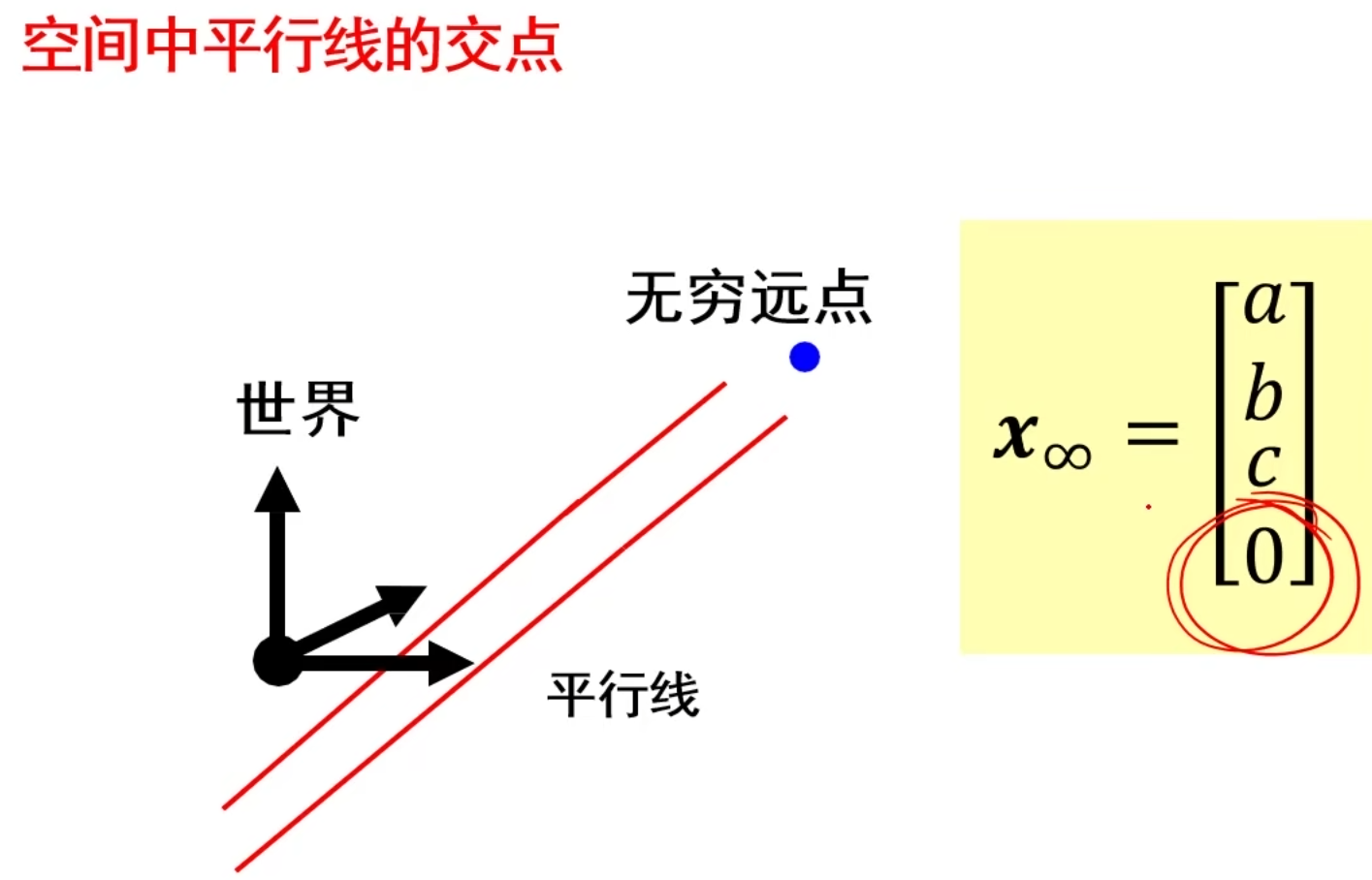
其中[a,b,c]就是3D空间中直线的方向向量
3D中的无穷远面
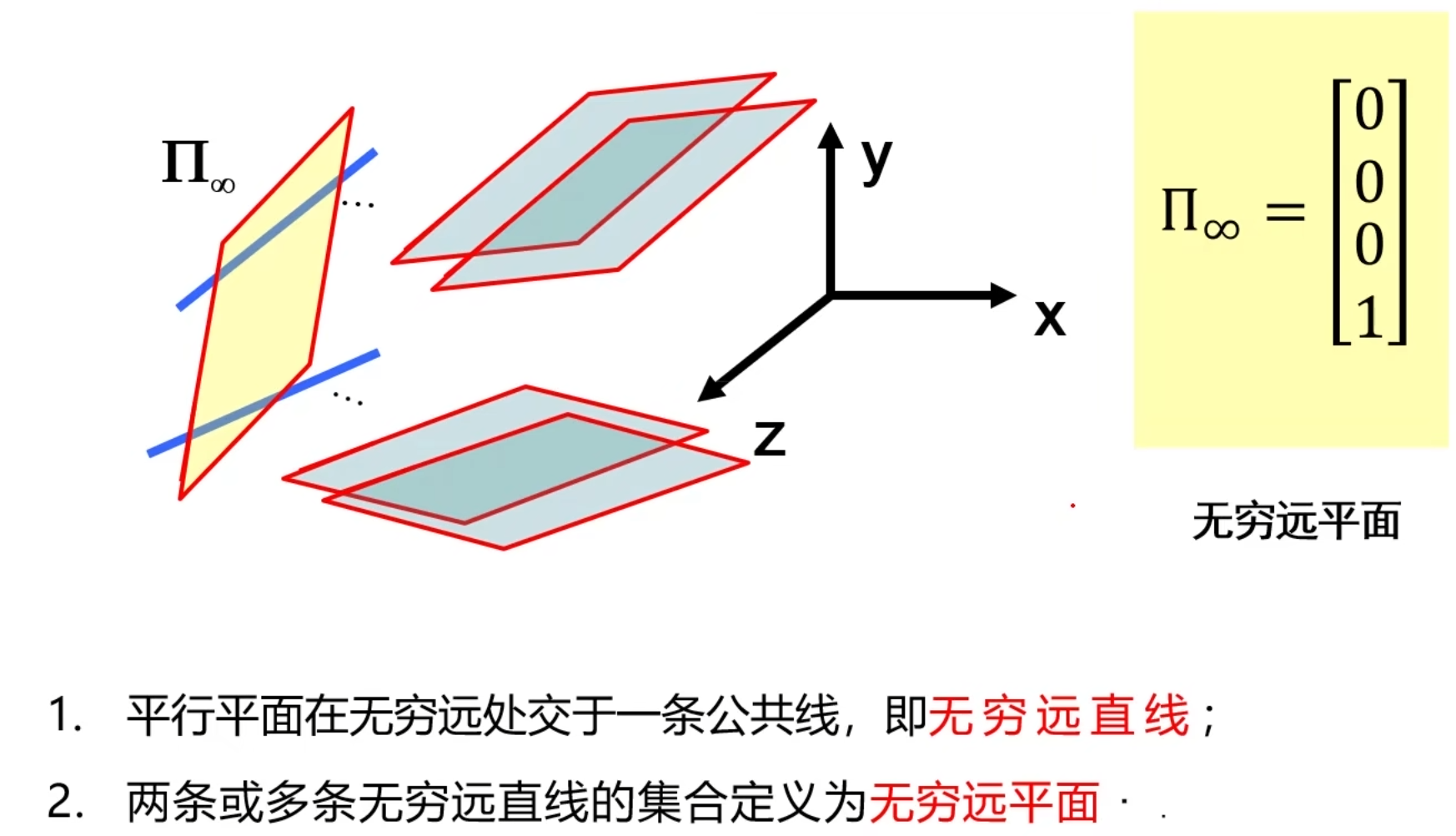
注意:3D中每一个平面都会对应一条无穷远线,所以各种平面的无穷远线合在一起就构成了一个无穷远面!
第二个角度,两个平行平面,会在无穷远处交于同一条无穷远线!
影消点和影消线
2D中无穷远点的变换
透视变换
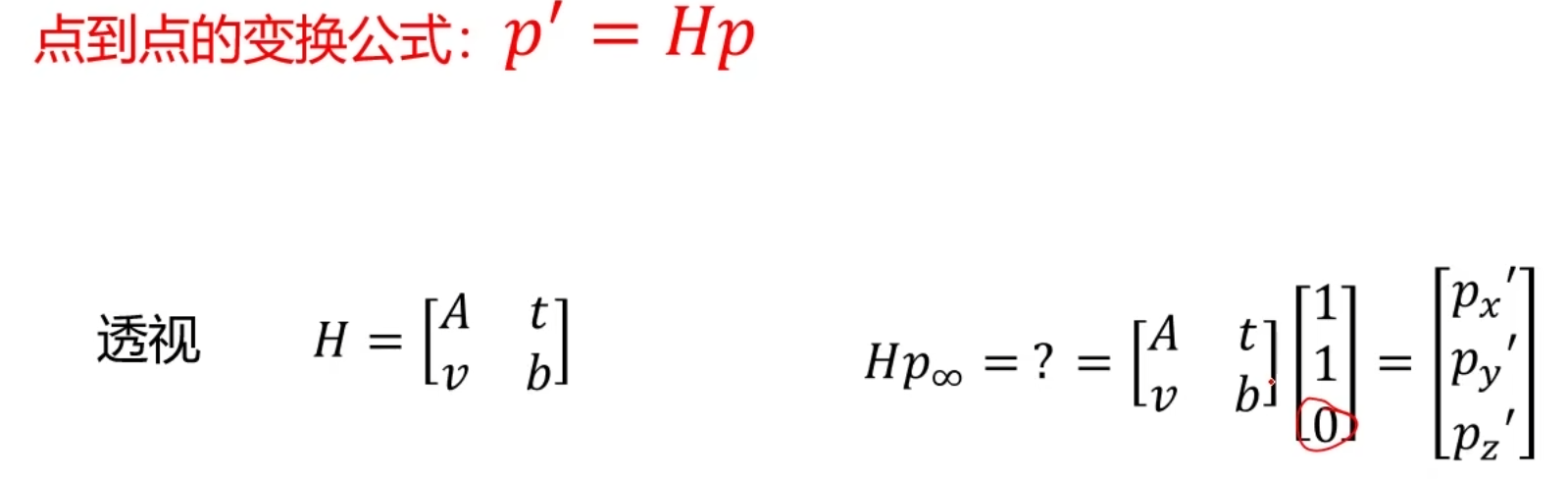
透视变换后,由于v是一个1x2向量,所以若v不为0,则无穷远点经过透视变换后不再是无穷远点
故透视变换不能保证无穷远点仍然是无穷远点
仿射变换
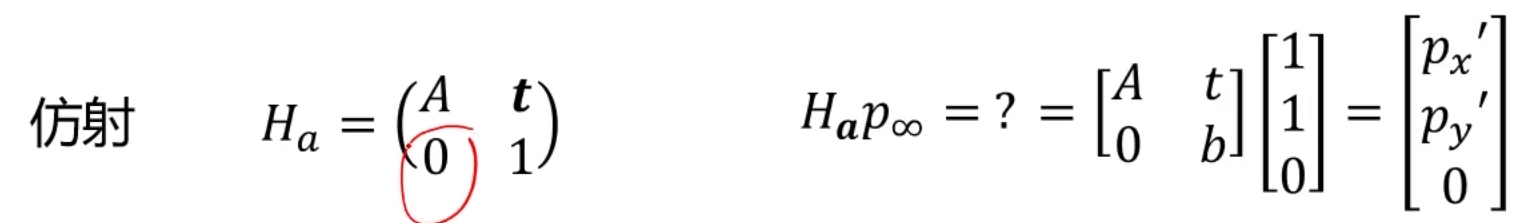
仿射变换后,无穷远点仍然是无穷远点
2D中无穷远线
2D中线的变换矩阵推导
线的变换需要通过点的变换解出
已知:直线l和点的变化矩阵H
求解:变换后的直线l^'^
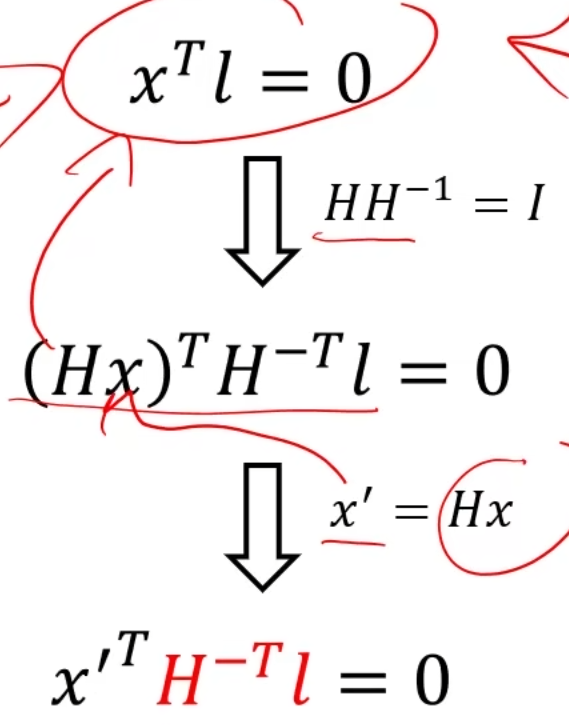
对比已知条件的最后一条,可以得到结论:
2D中无穷远线的变换
透视变换
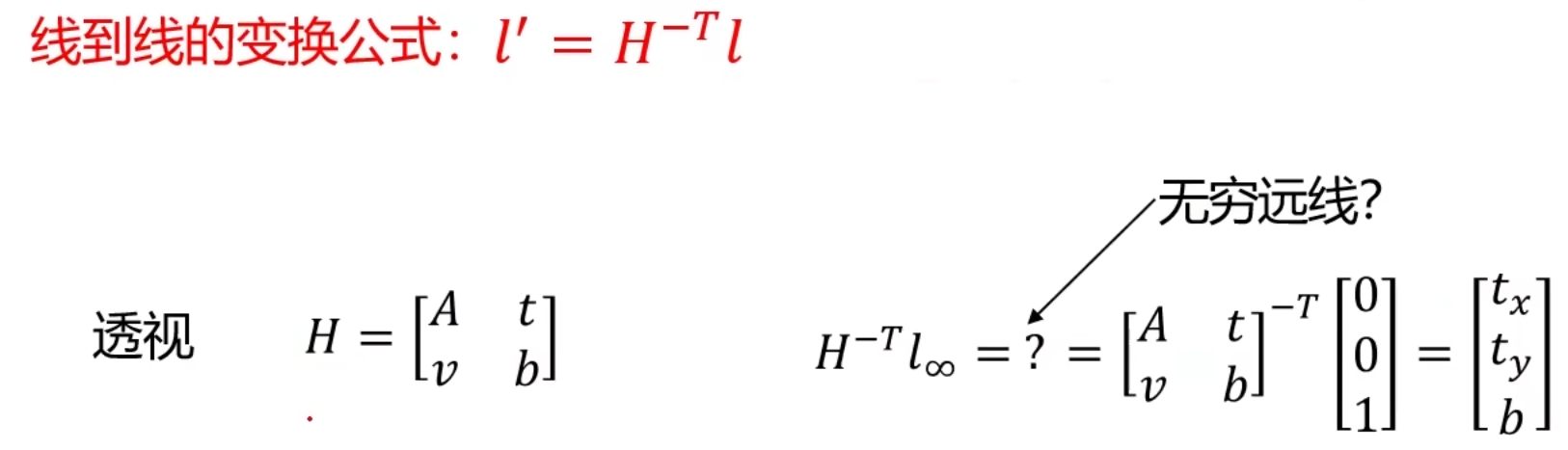
透视变换后,不一定能保证得到无穷远线
仿射变换
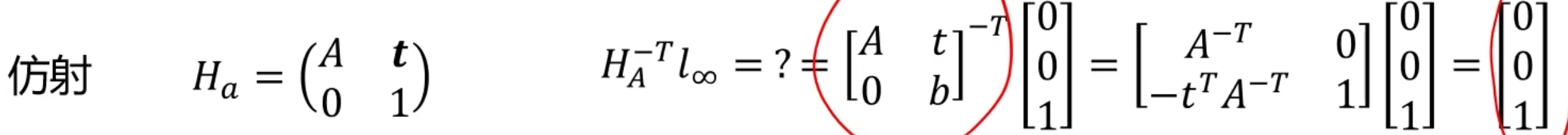
仿射变换后,可以保持还是无穷远线
影消点
三维的无穷远点,经过相机摄影,得到二维像素图像平面上的一个投影点,就叫影消点(像素坐标)
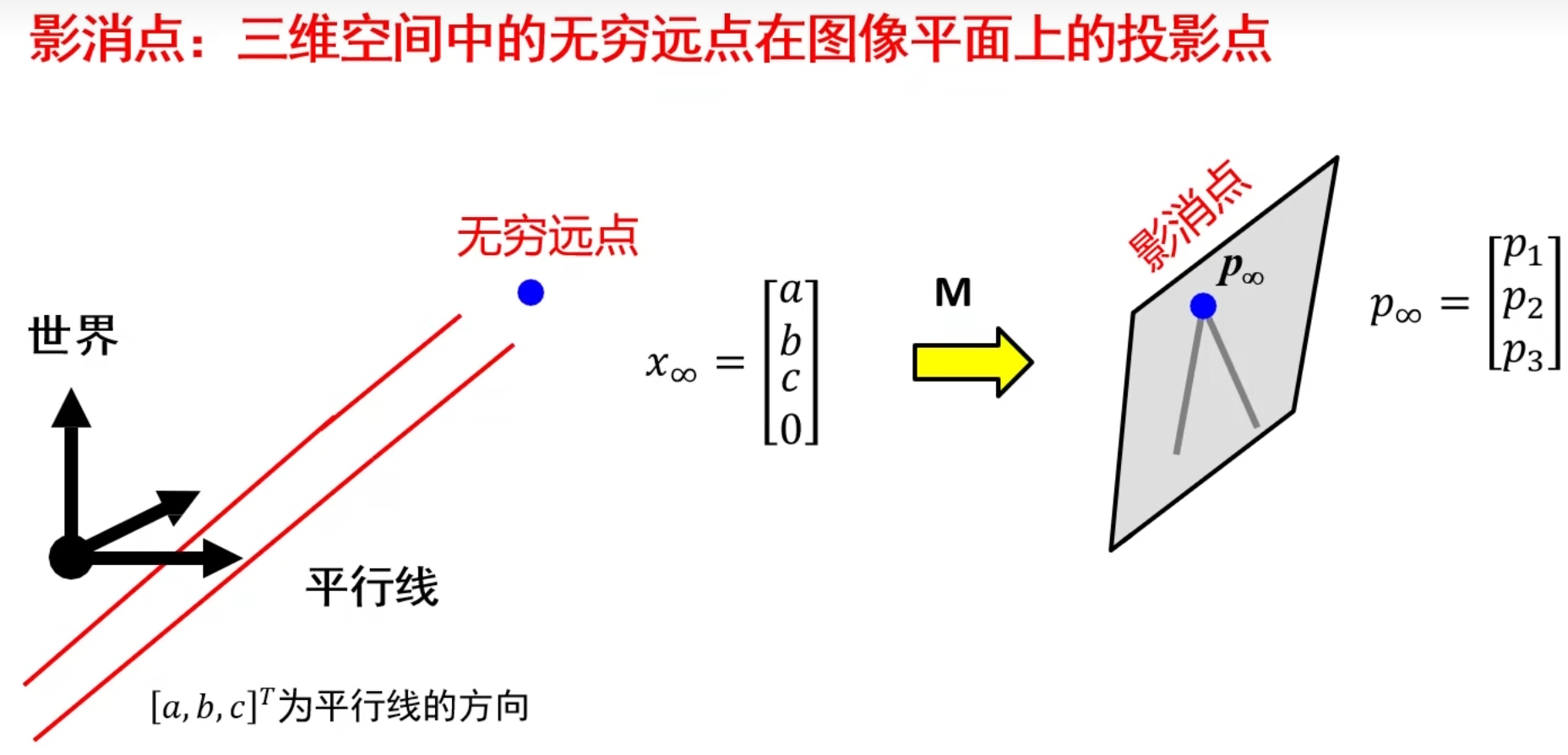
影消点与摄像机空间下三维直线的联系
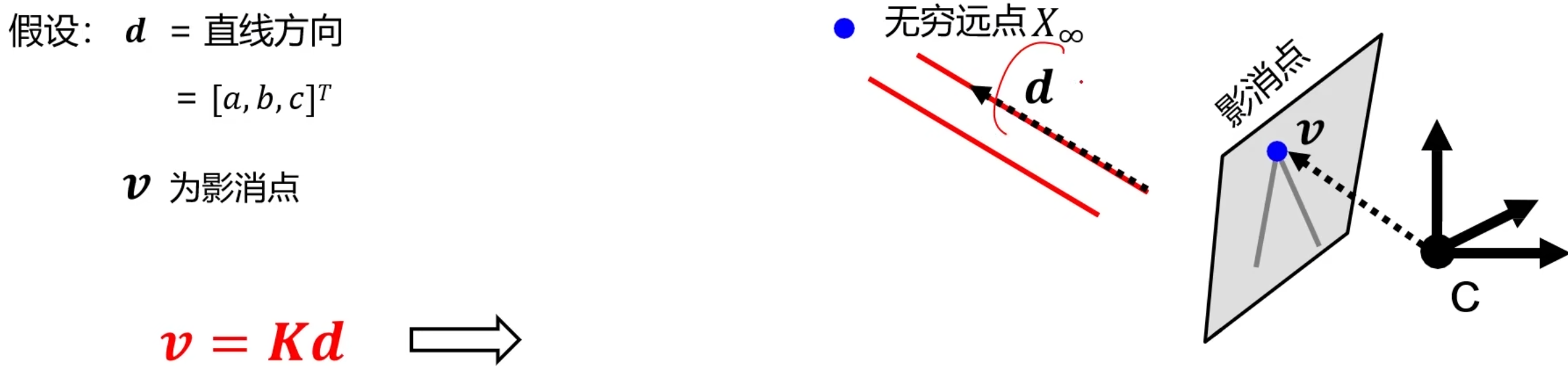
这里的K是摄像机内参数矩阵K
这里的结论是,影消点v和相机空间下直线方向向量d有K矩阵的关系
注意:这里的我们不考虑摄像机外参数矩阵,因为三维的直线是在相机空间下的,我们不关心世界空间!
继续可根据K和v算出相机空间下直线方向向量:
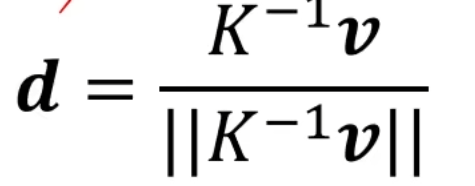
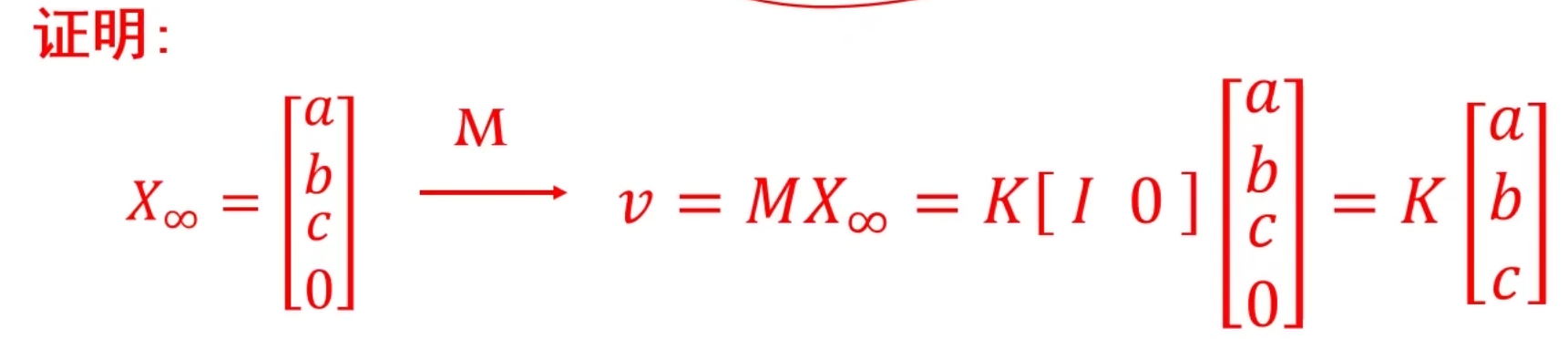
影消点是三维空间下一组平行线交出的无穷点在像素图像中的投影点。因此给出内参数矩阵K和一个影消点的坐标,我们就可以推出相机空间下一组平行线的方向向量,以及其无穷点的坐标
影消线
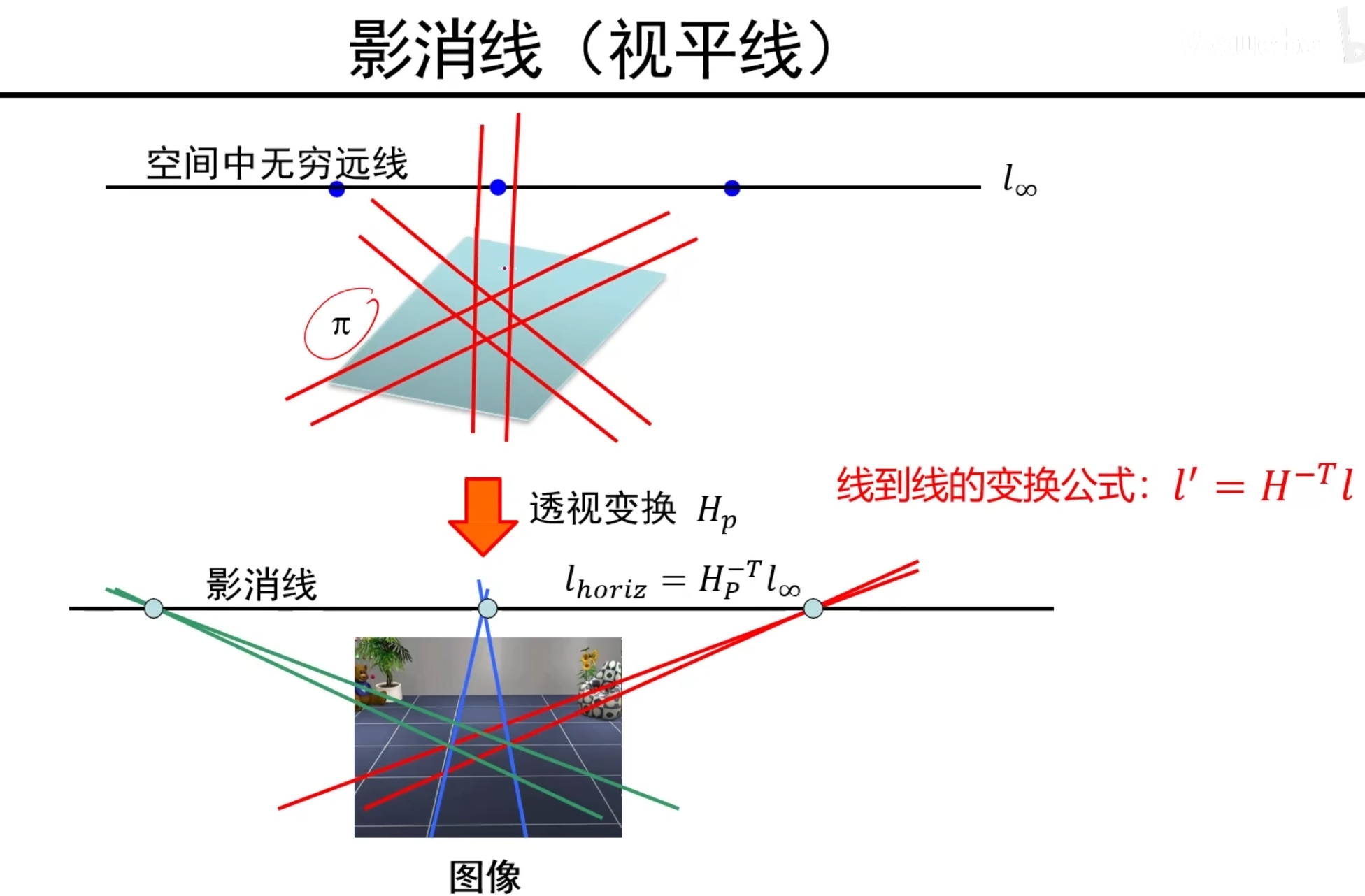
将三维空间的无穷远线经过线的透视变换(该透视变换其实就是之前推的相机的投影矩阵M,但是M是针对点的变换,对于线的变换,取其逆转置)以后,得到一条不是无穷远线的像素平面中的线,这条线就是影消线,影消线上的每个点都是影消点

通过已有知识,很容易明白橙色的线是影消线
影消线和平面法向量
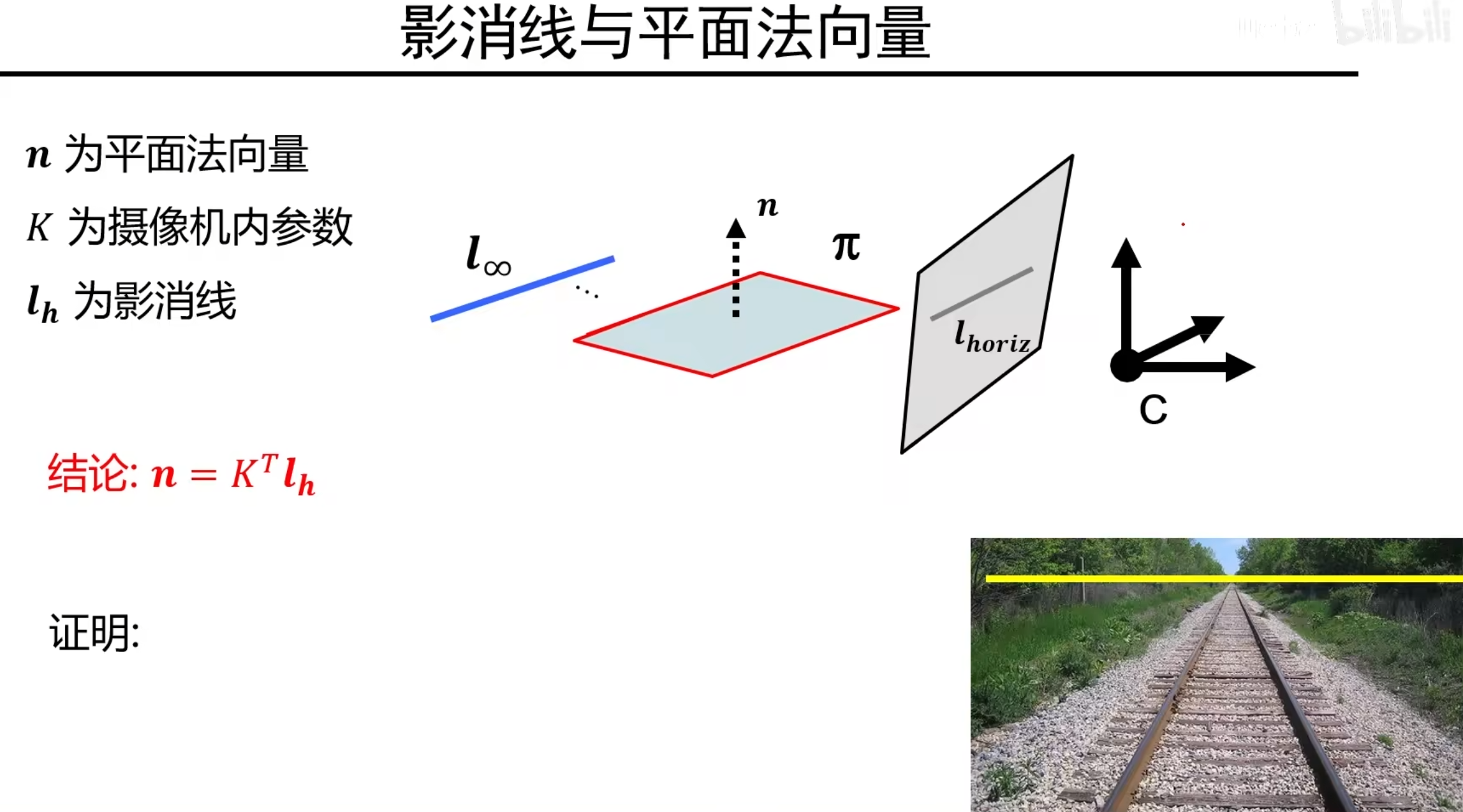
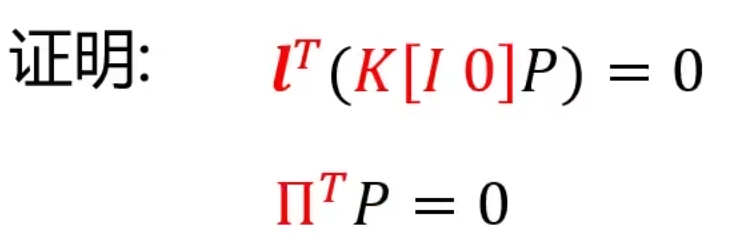
已知K,l~h~,我们如何求出一个平面的法向量(求出法向量就相当于求出了平面)?
一个平面一定对于一条无穷远线,无穷远线变换后得到一条影消线,因此,一个平面就对应一条影消线
关于证明的说明:P是相机空间中的一个三维点,而且该点是无穷远线上的一个无穷远点,所以经过内参数矩阵变换后就得到一个影消点,该影消点一定在影消线上,所以有证明中第一行的等式。同时,P点属于我们要求的平面,所以有第二行等式(Pi就是平面的参数向量[a,b,c,d])。
影消点和影消线总结
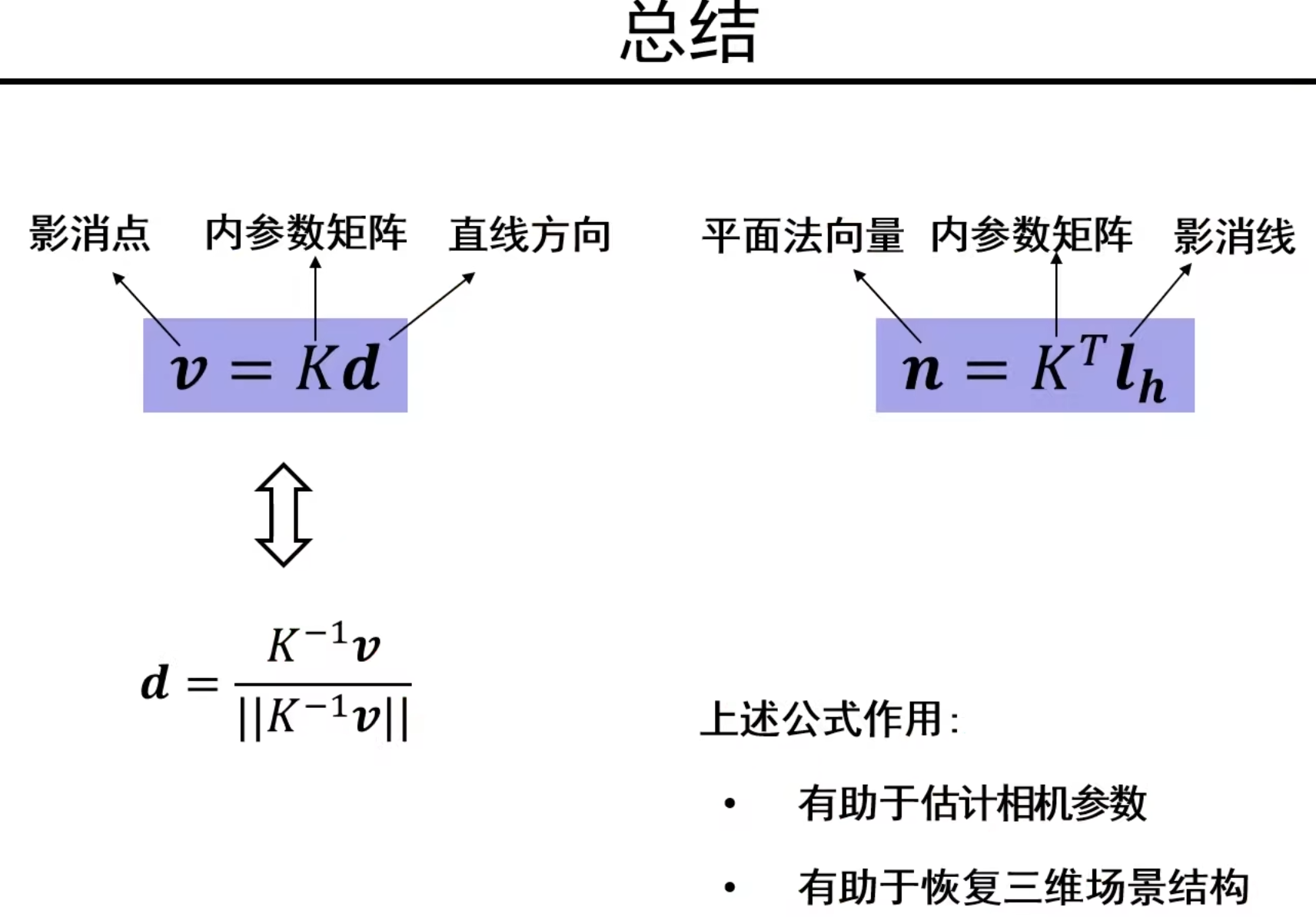
单视重构
两组平行线的夹角与影消点
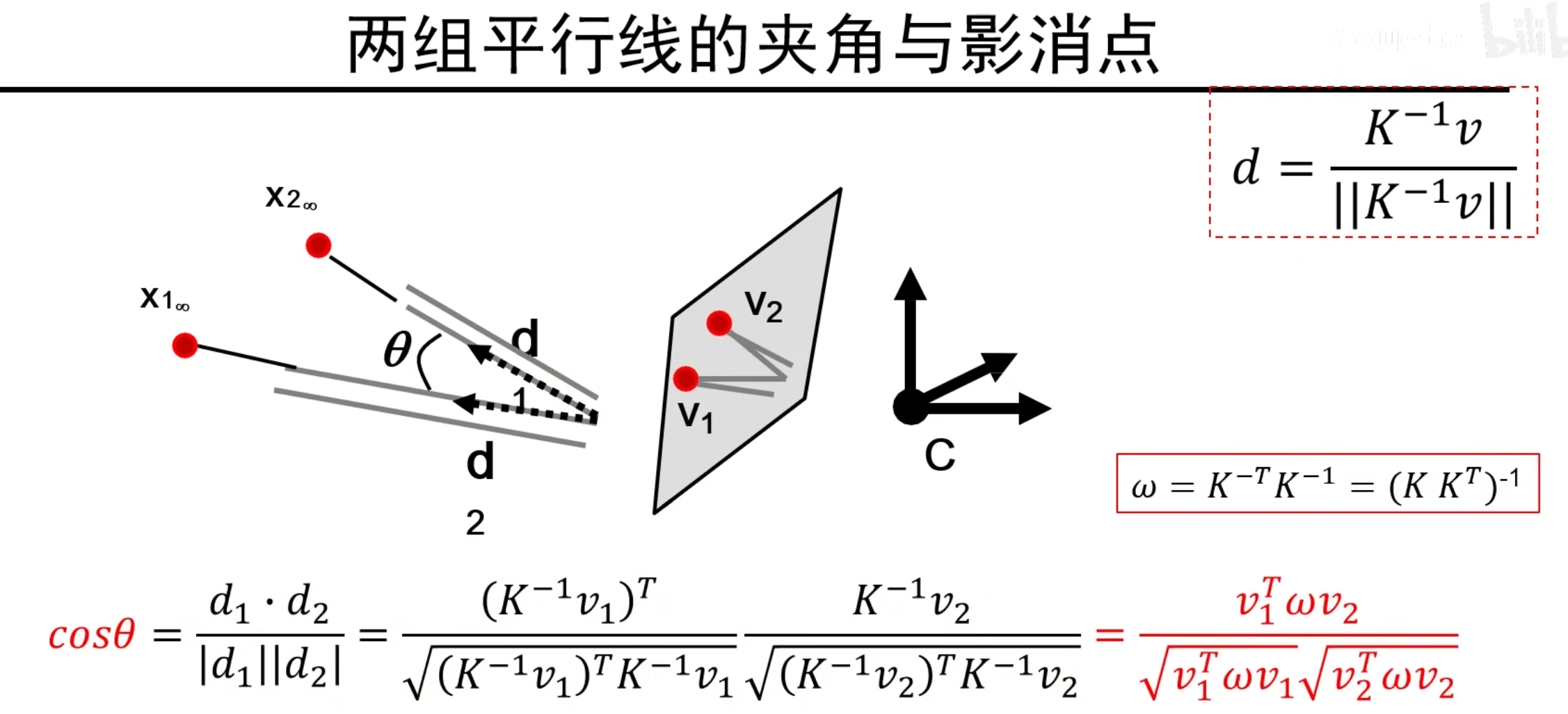
说明:v1,v2是影消点,两个d是相机空间下的两组平行线的方向向量,θ是两组平行线的夹角,K是内参数矩阵。
定义一个w进行化简整理
这有什么用呢?
观察,可以发现

我们先来看,w有什么性质
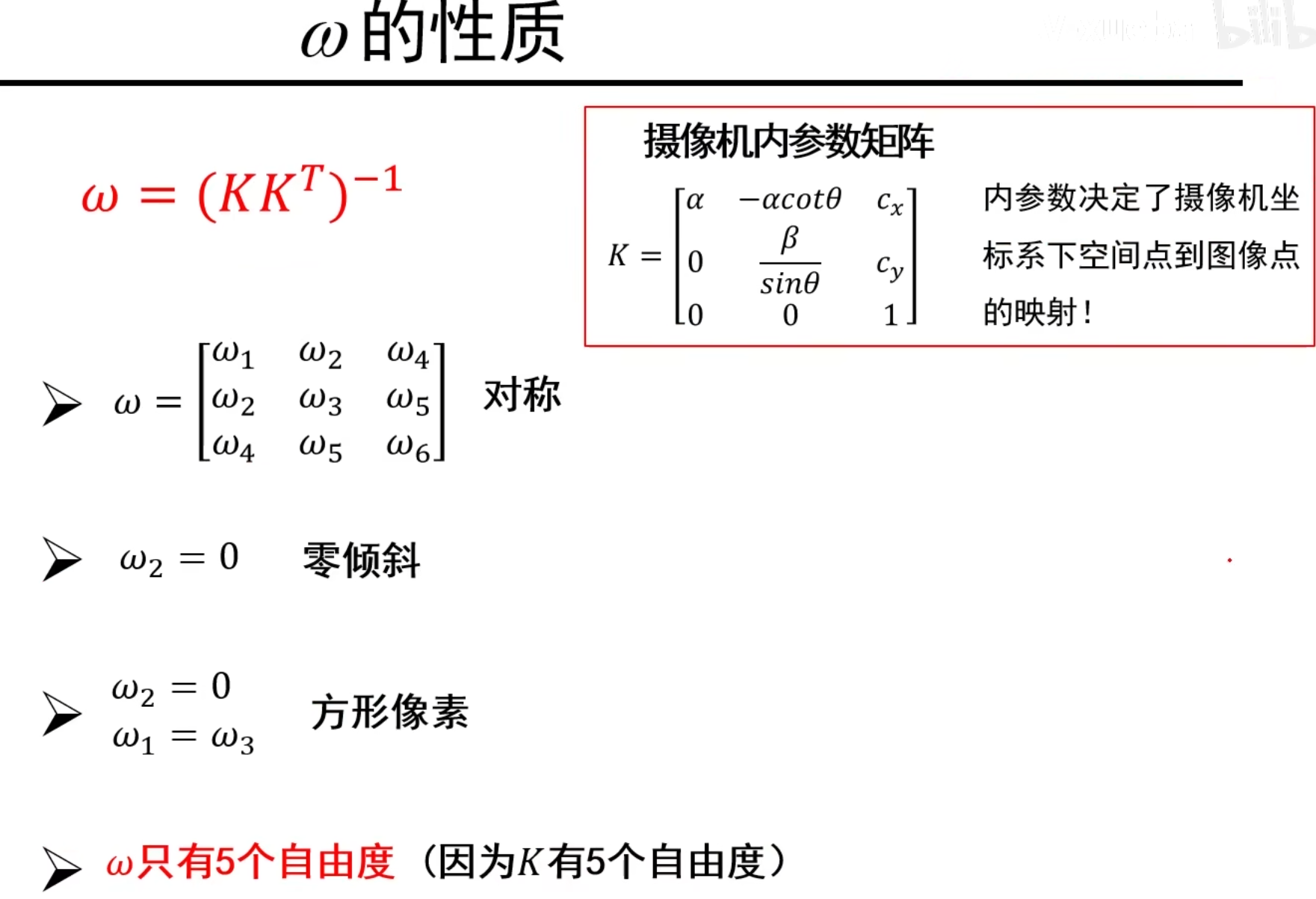
说明:把K矩阵代入w表达式中,观察底下的性质即可
w~2~ = 0,就表明θ = 90°,也就是零倾斜
w~2~ = 0 且 w~3~ = w~1~,表明 α = β,也就是方形像素
单视图重构的例子

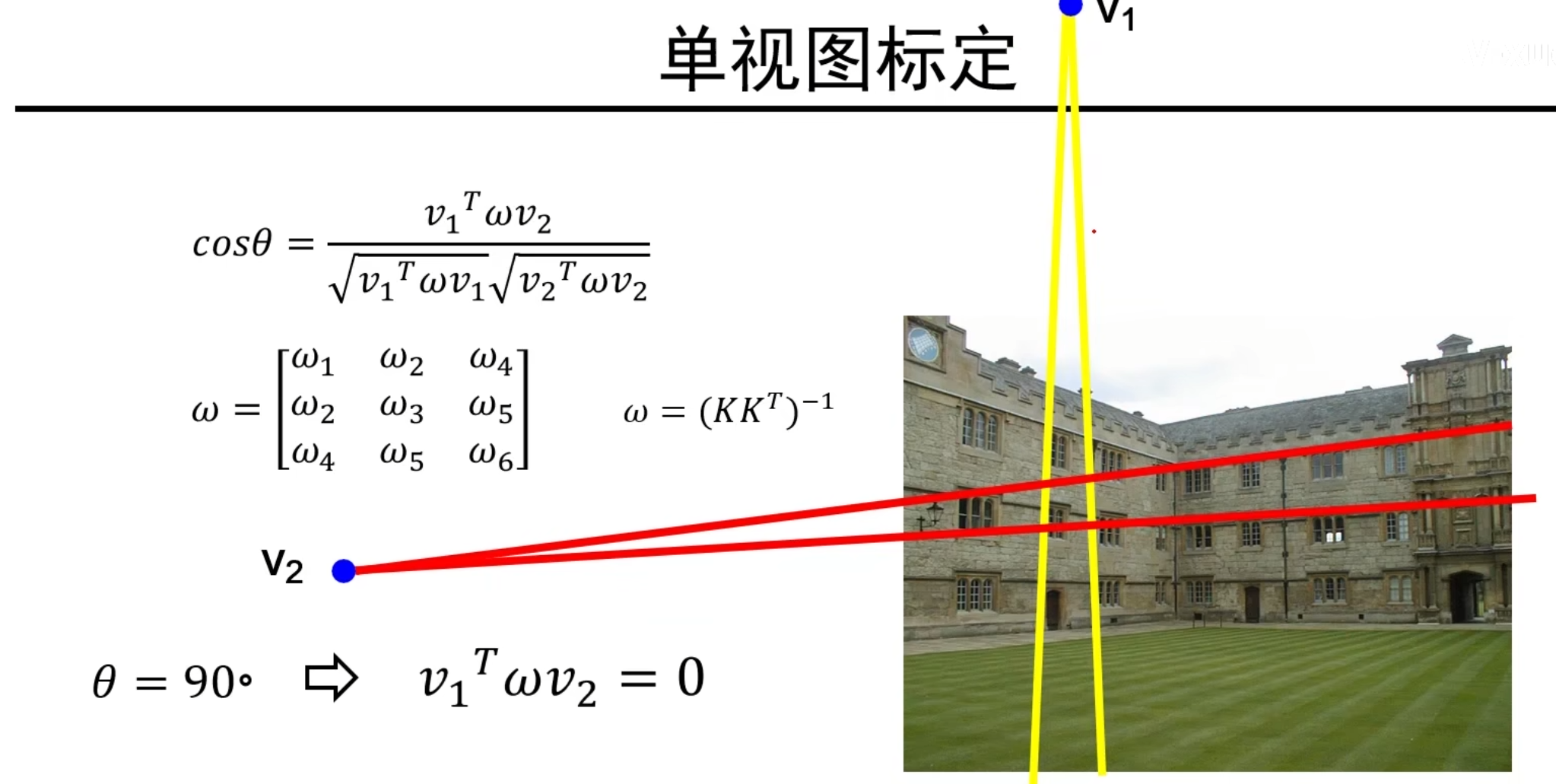
说明:我们按照刚刚讲的东西,去找两组平行线,这里取竖直窗户的一组平行线和水平窗户的一组平行线,很容易知道这两组平行线的夹角是90°,所以可以得到上图中的等式
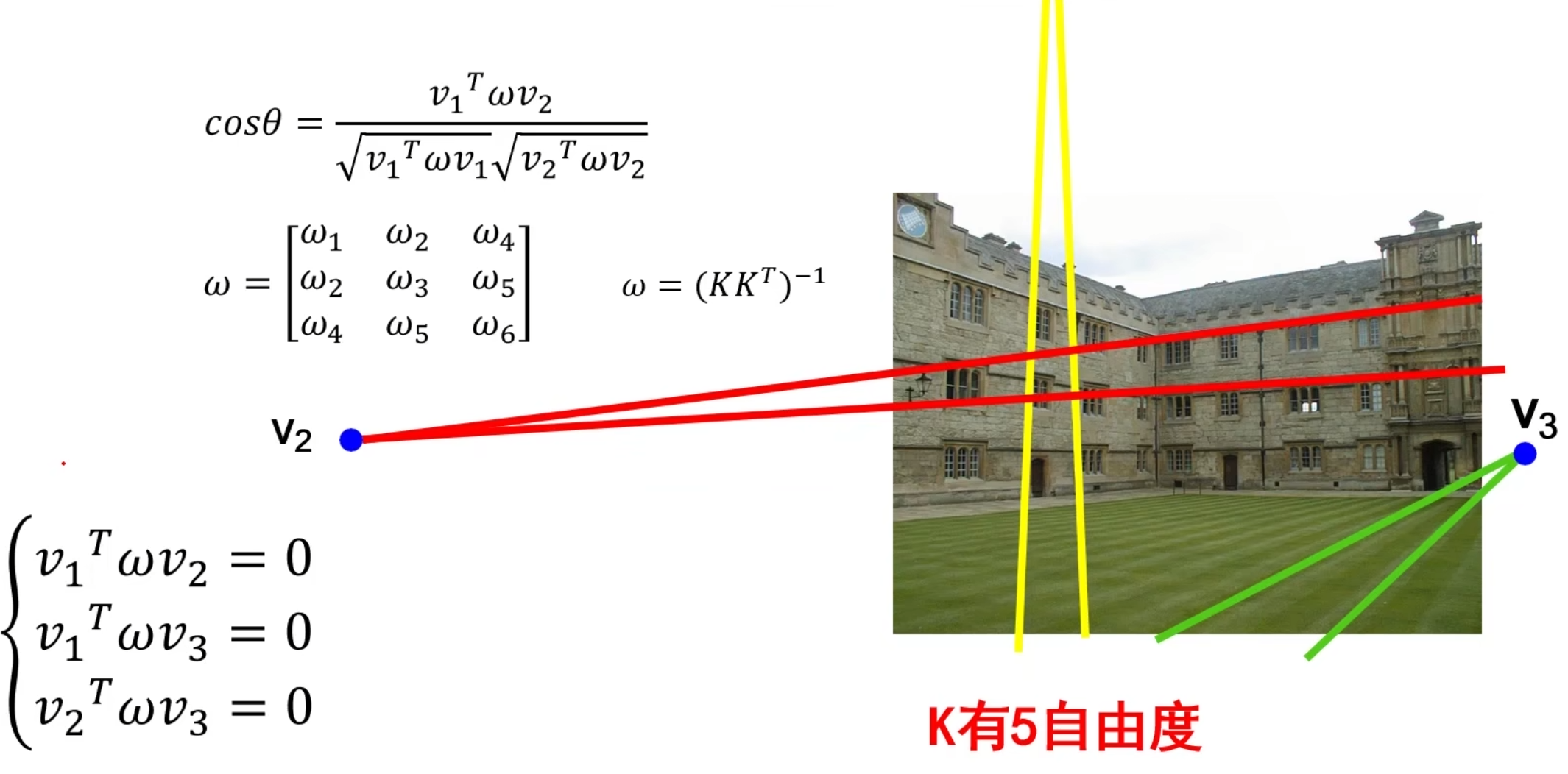
再加一组平行线,图中三组平行线两两垂直,就可以得到三个等式
但是我们知道K有五个自由度,所以是求解不出来的!
怎么办呢?
此时,我们给定两个假设:

这样,θ就是90,且α = β,相当于减少了两个自由度,我们可以解出K了!
我们使用了影消点和线的关系,但是还没有使用影消线和面的关系,接下来使用。
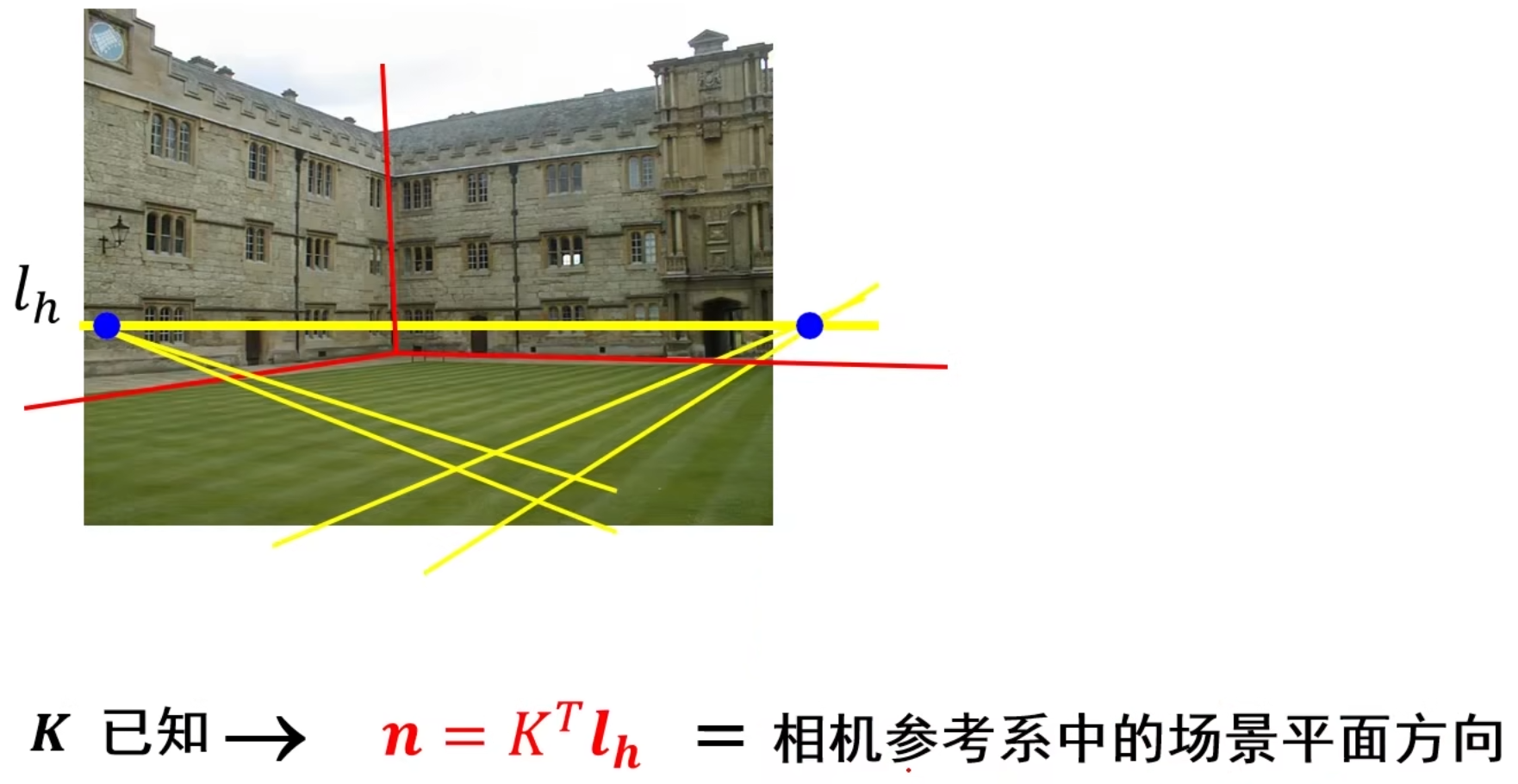
说明:影消线l~h~是草地这个平面对应的影消线。刚刚我们已经算出了内参数矩阵K,此时就可以根据影消线和面的关系求得草地这个平面的法向量,相当于我们通过一张图把草地这个3D平面重构出来了。同理,我们可以重构出所有面,也就是整个场景!
单视重构存在的问题
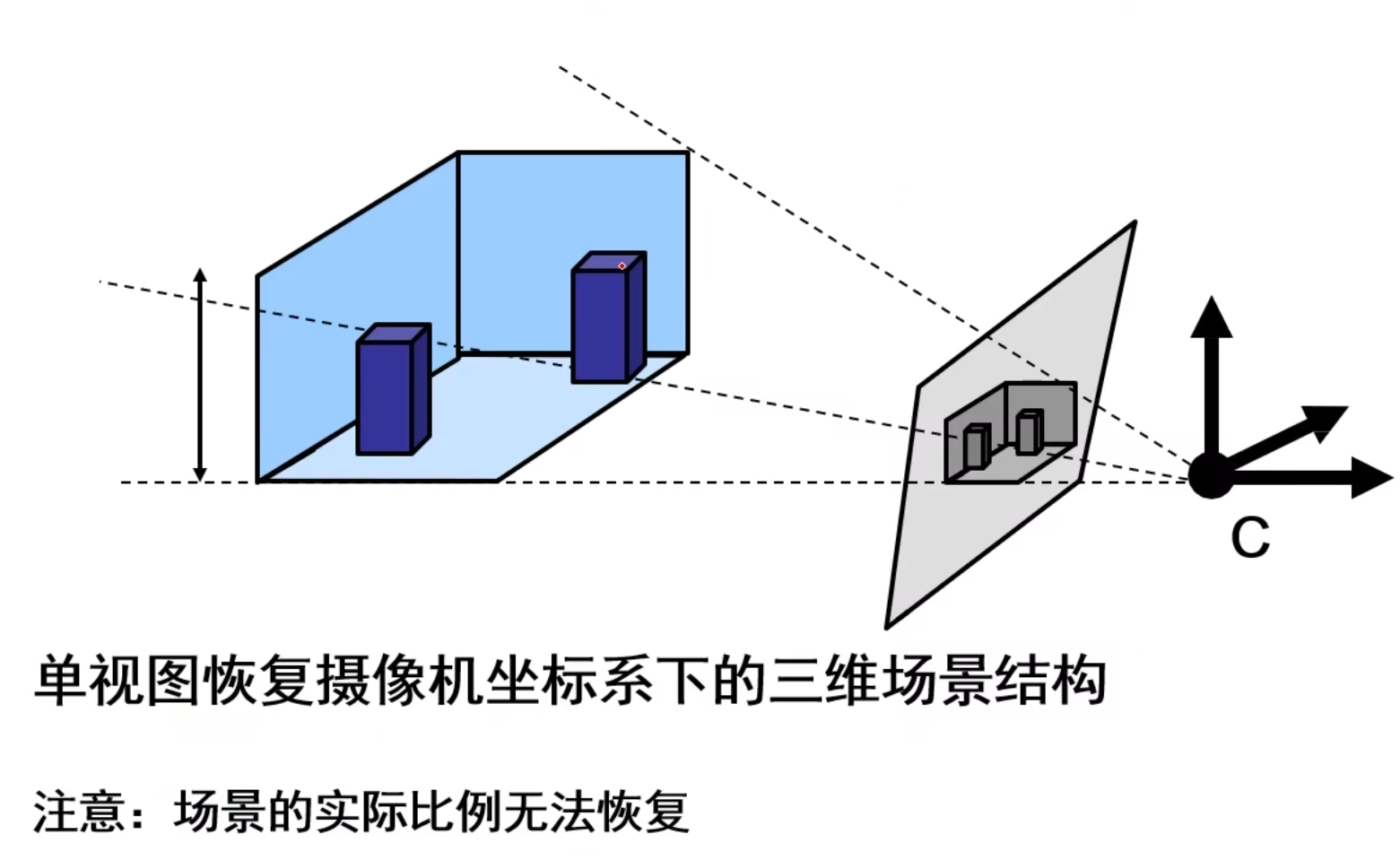
真实场景和重构场景的比例我们无法得知,因为我们完全没有考虑世界空间。
同样,真实场景的位置,朝向等都无法得到
同时,要想进行重构,我们还需要先验证图片中的影消线,影消点等等关系,这都是弊端。
(待填坑)课外补充内容——计算机视觉的图像匹配

4.三维重建基础和极几何
三维重建基础
为什么从单视图恢复三维结构不够普适,因为无法确定深度可见如下图:

为了解决这个问题,我们使用两个眼睛来解决这个问题。
三角化
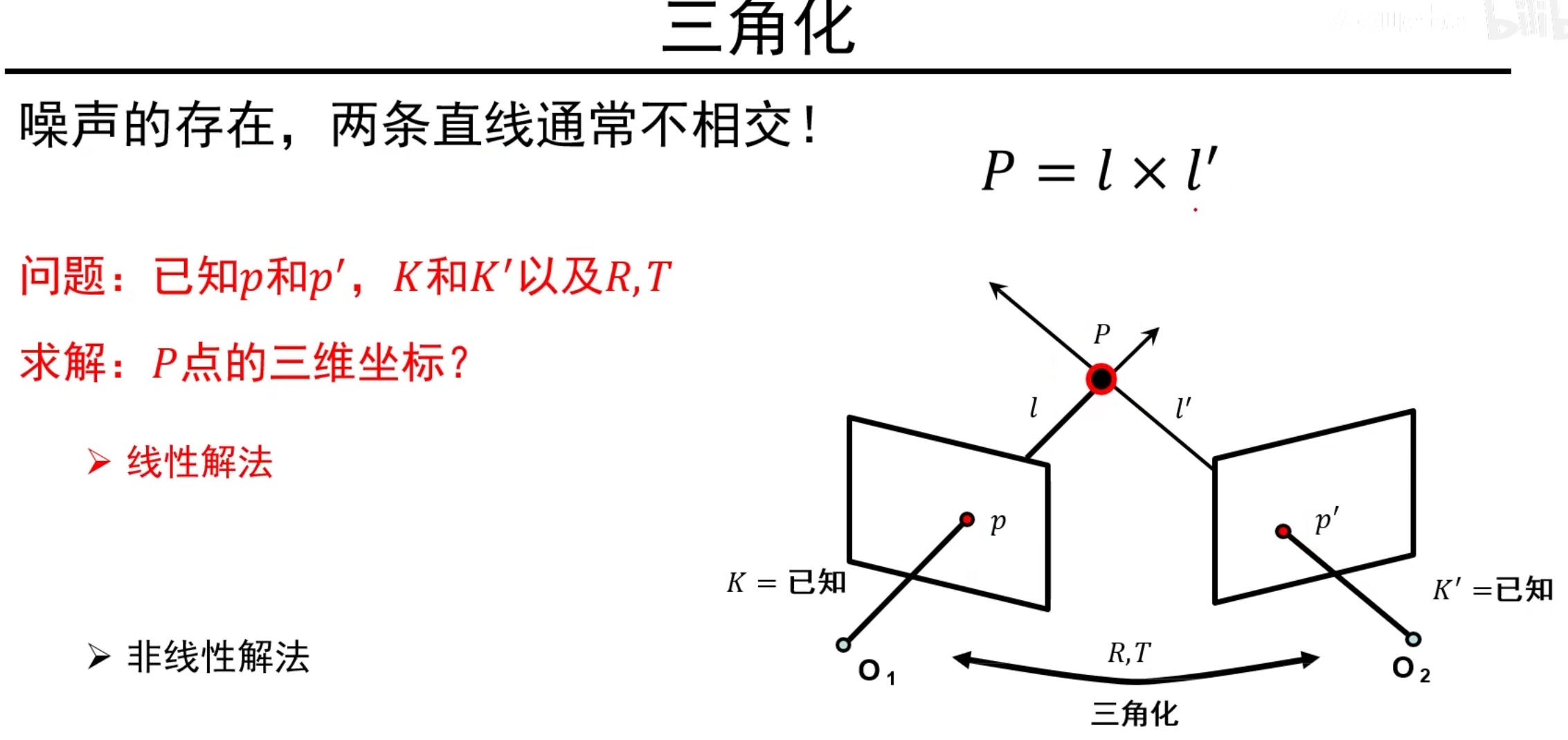
对于两个摄像机拍摄画面,我们认为p和p^'^对应的是同一个点,为了通过像素平面的点确定三维空间的交点,我们需要首先通过影消点与三维线关系得到线的向量,再把o~2~摄像机坐标系通过R,T旋转平移变换到o~1~坐标系,这样就可以使用线叉乘得到三维下交点P的坐标,这个过程就叫三角化。但是,噪声的存在可能导致两条空间线很难相交。因此我们改用一些近似方法来求解
三角化线性解法
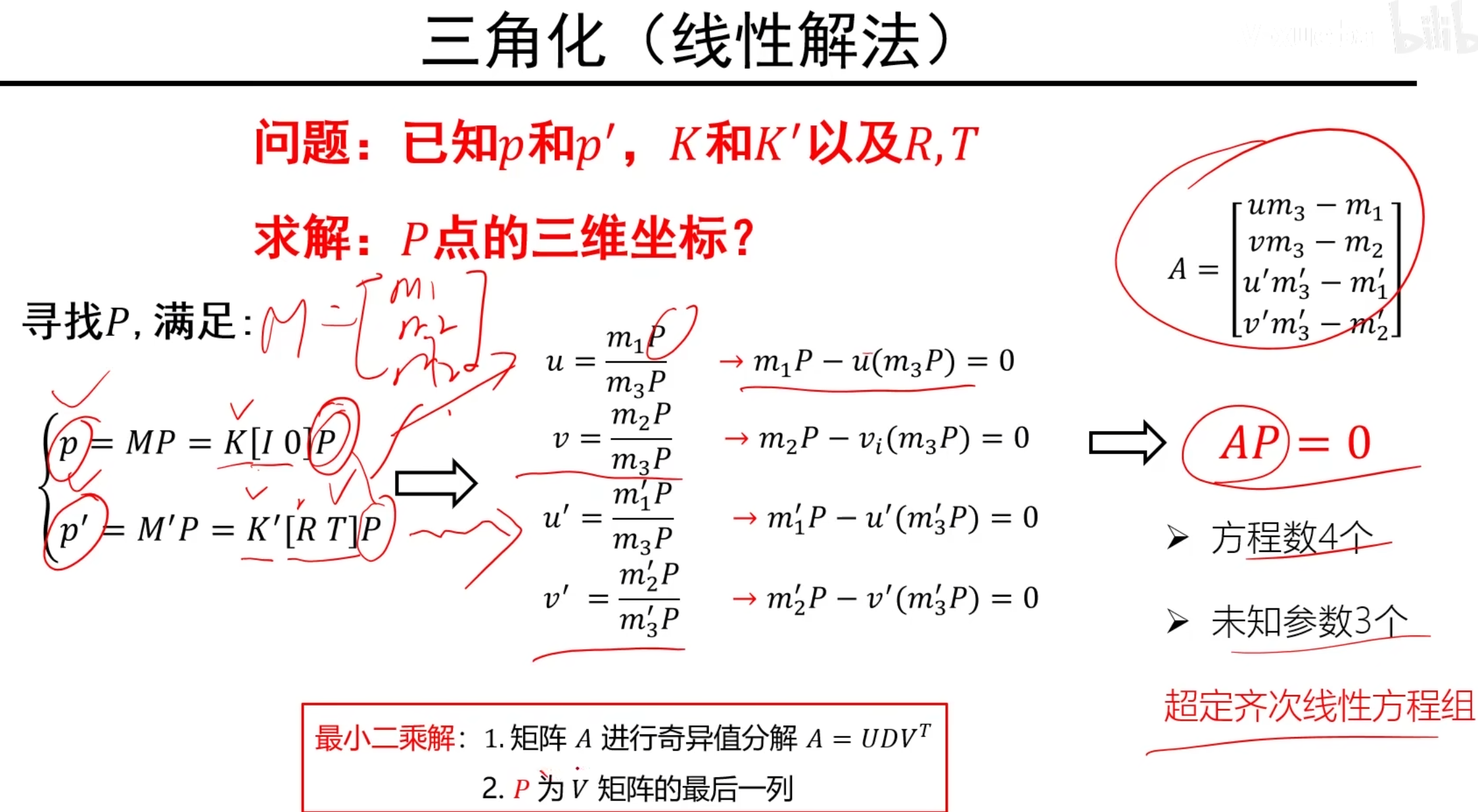
说明:用之前类似的方法,转换成齐次线性方程组,因为我们要求P,其他参数都是已知,所以是线性的。使用奇异值分解即可。
三角化非线性解法
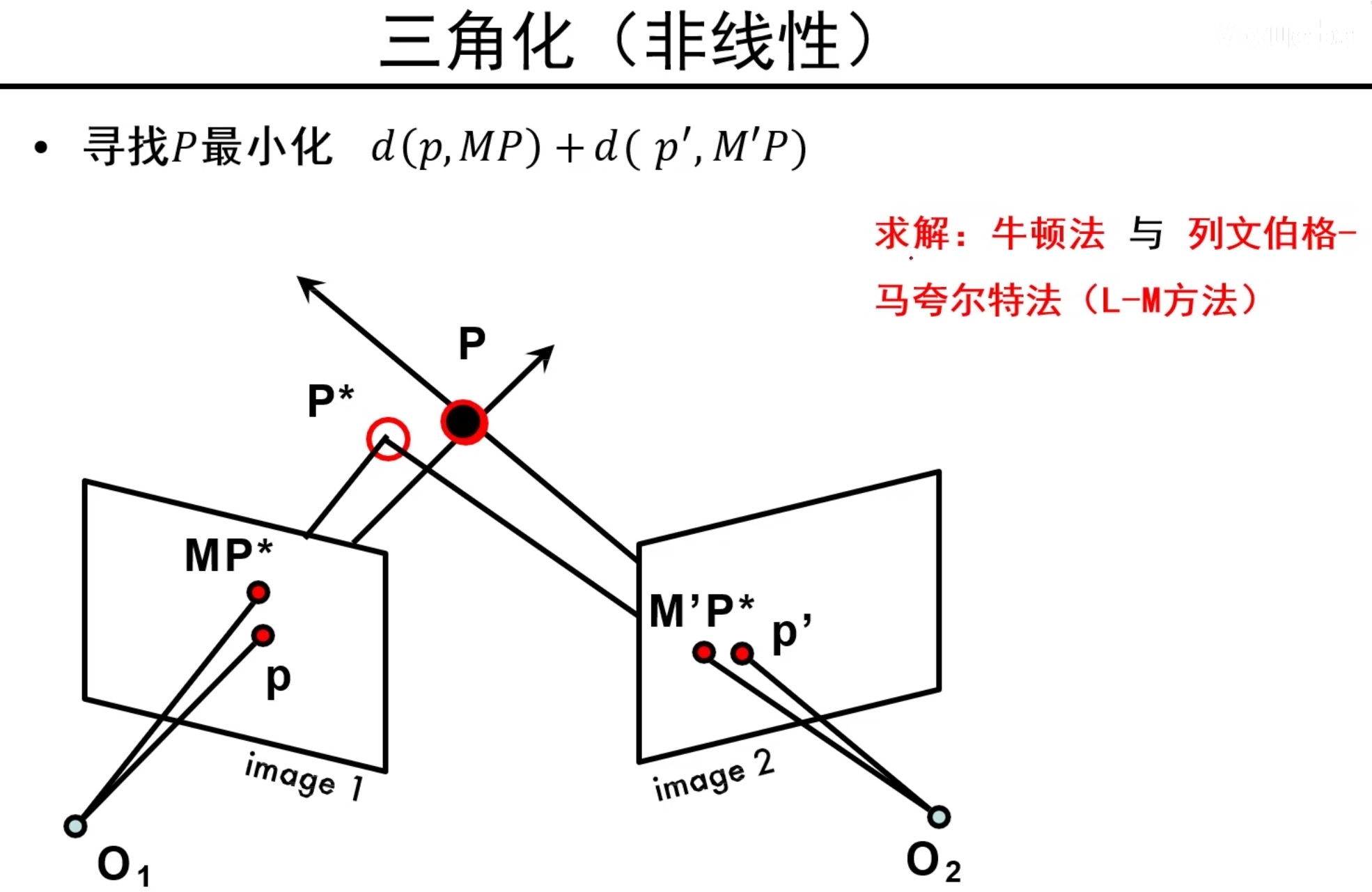
三角化的实际问题
想要三角化,必须知道两个摄像机的K,K^‘^,以及像素平面的一对p,p^’^,我们通过之前的标定方法可以获得内参数矩阵,但是我们如何得到一对p点呢?由此,我们引出极几何和基础矩阵来解决。
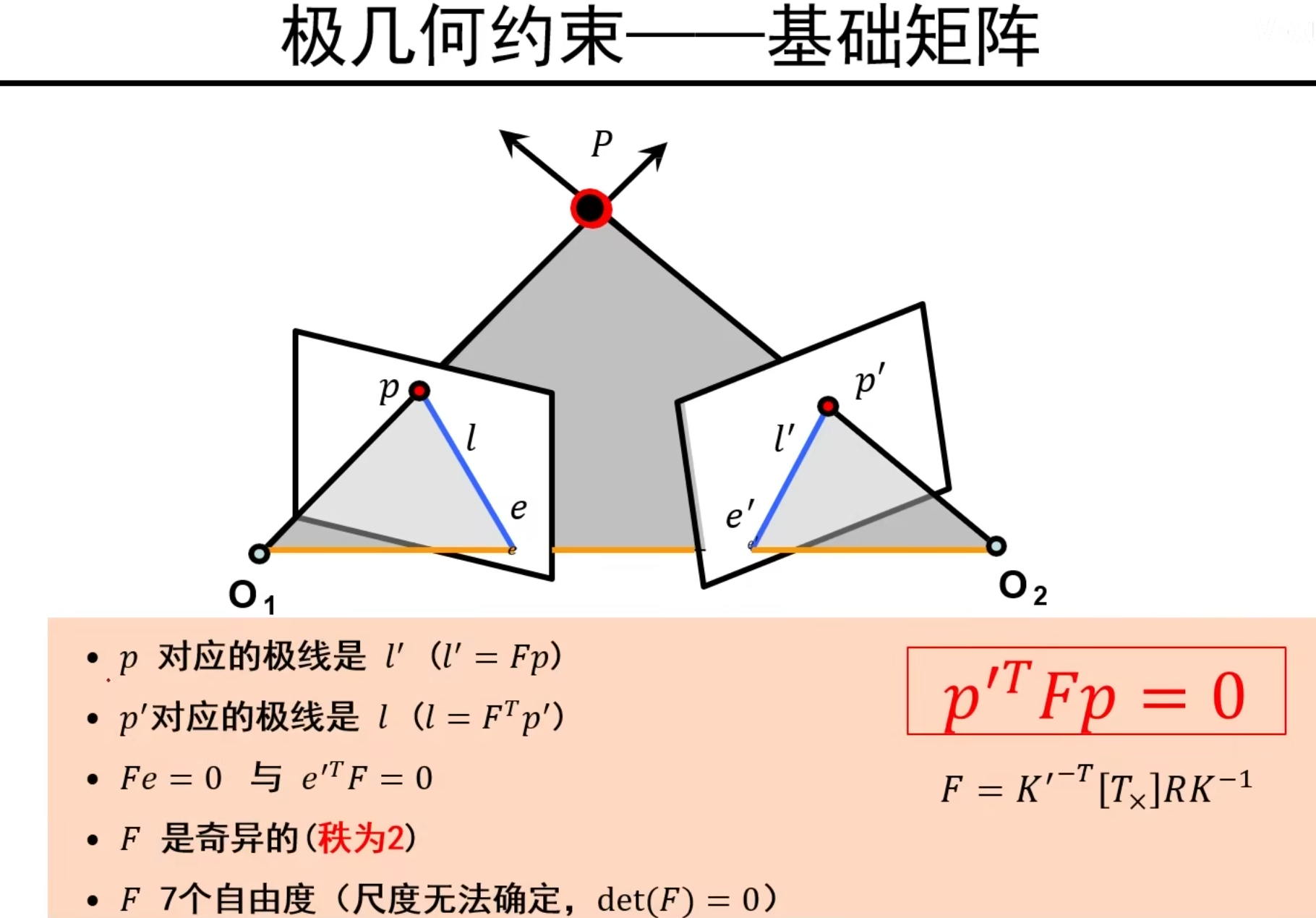
极几何及基础矩阵
极几何描述了同一场景或者物体的两个视点图像间的几何关系
极几何基础概念
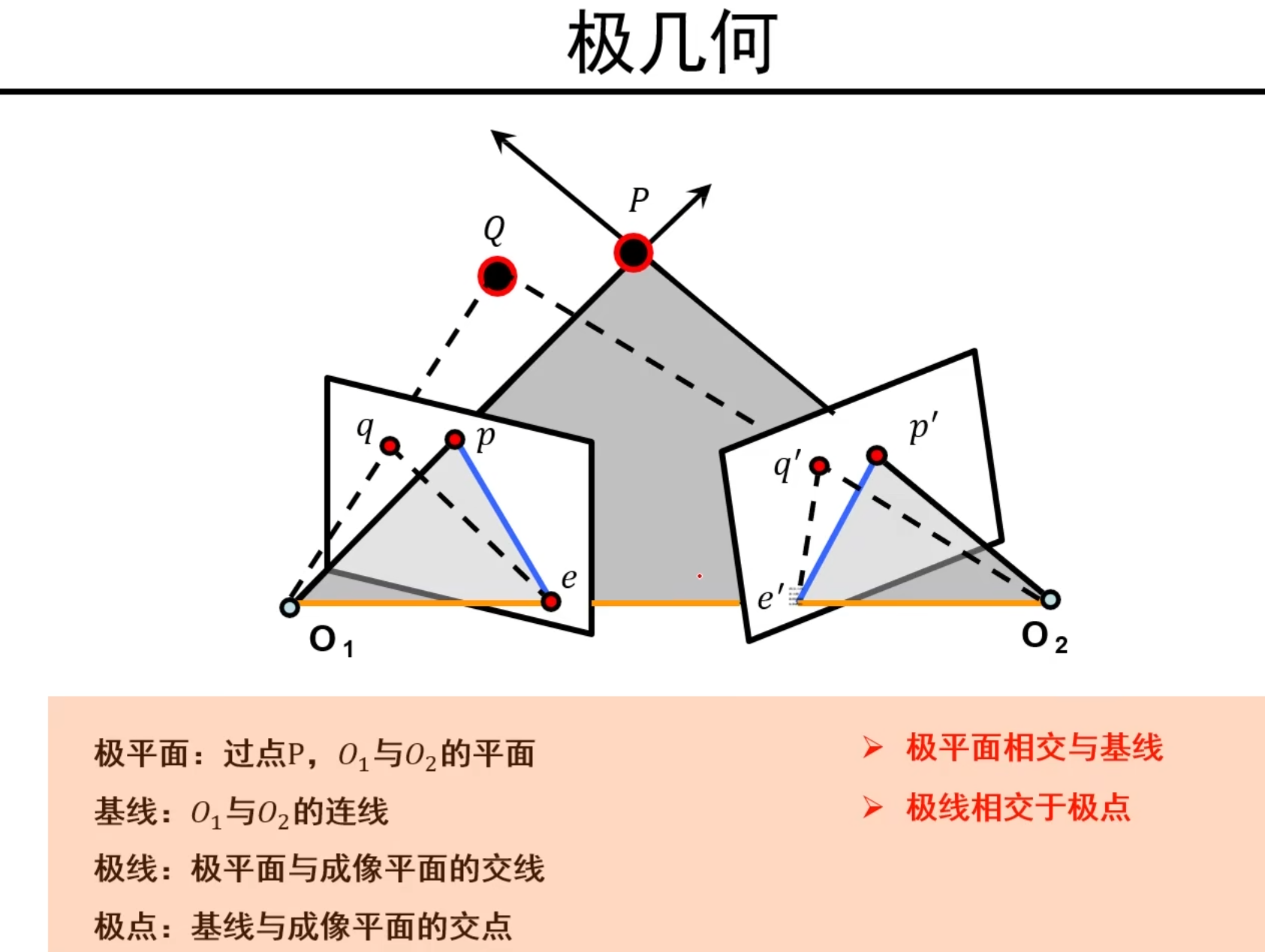
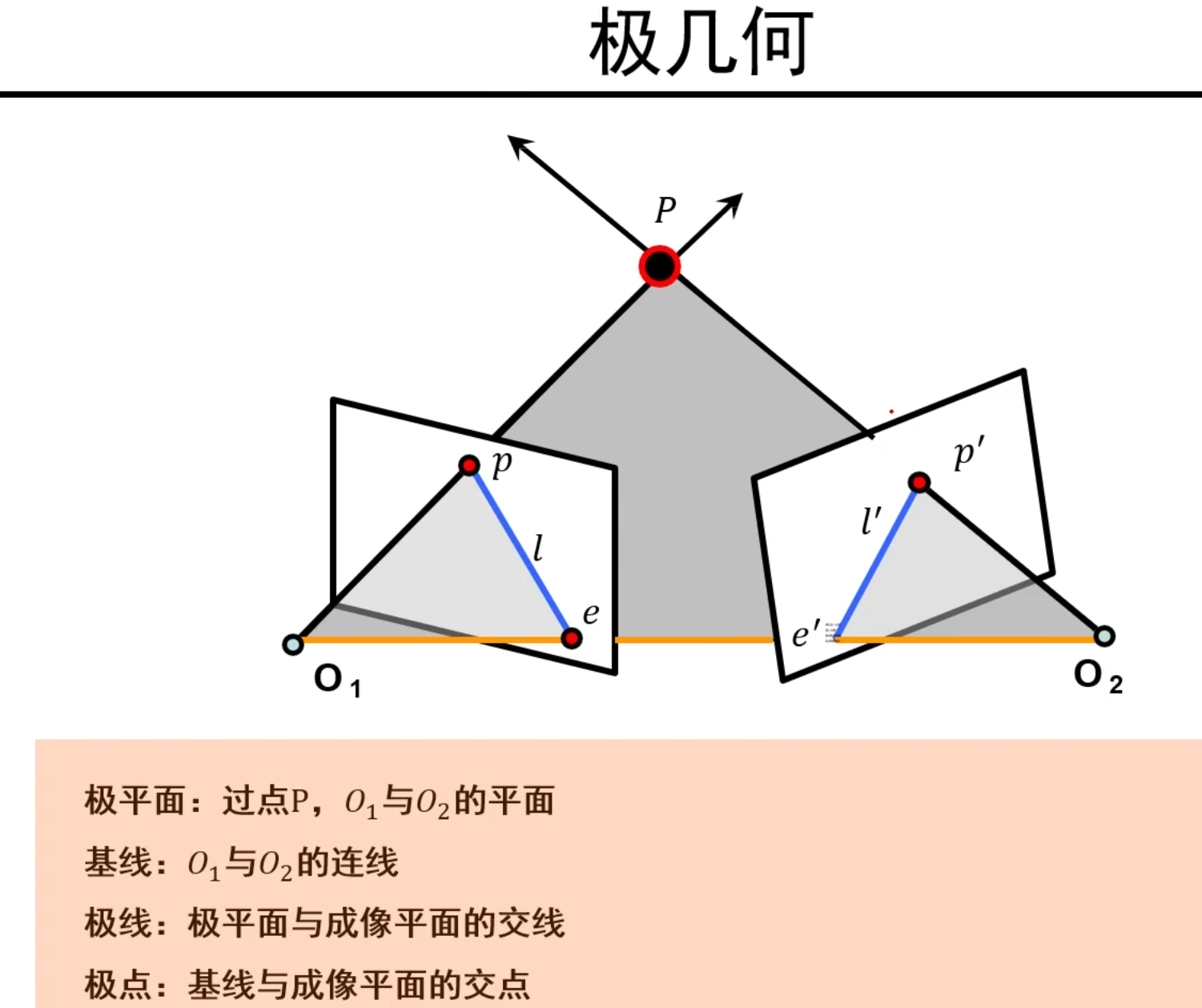
说明:极线是图中蓝色的l和l^‘^,极点是图中的e和e^’^
平行视图——极几何特例
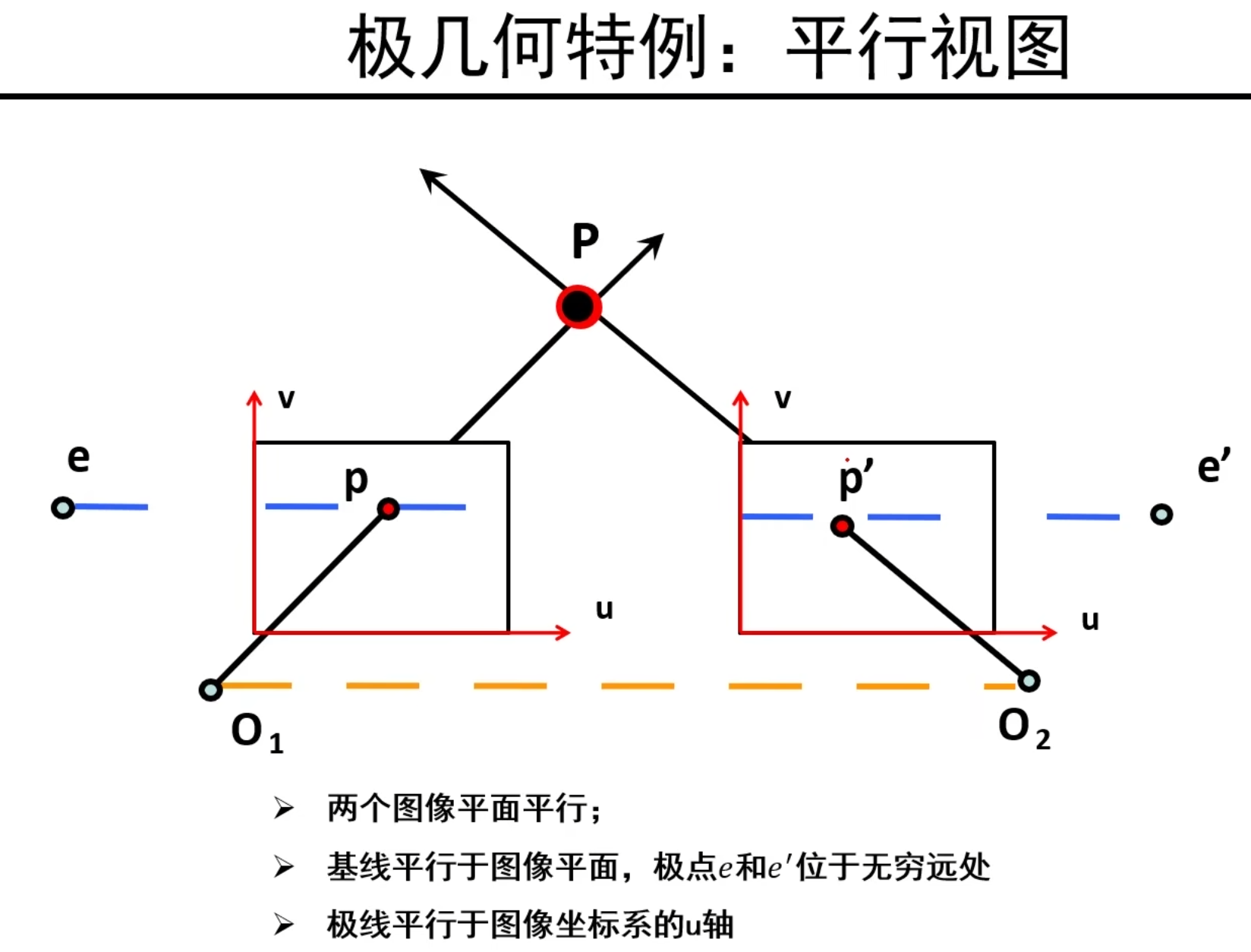
前向平移——极几何特例
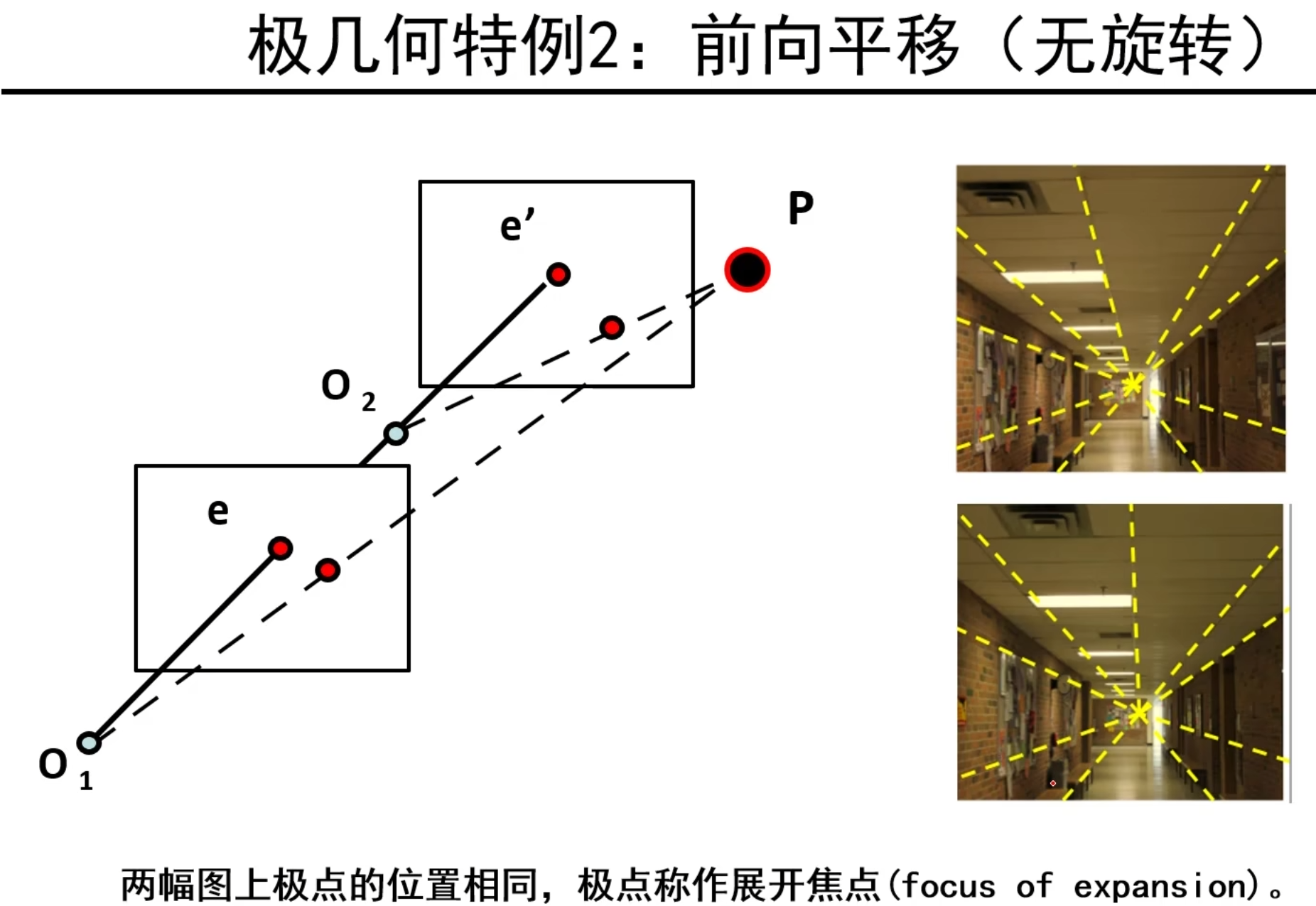
本质矩阵
本质矩阵是对规范化摄像机拍摄的两个视点图像间的极几何关系的代数描述
规范化相机:M矩阵是类单位阵,3x4的M阵前3x3是一个单位制,最后一列为0,可以回顾第一节课
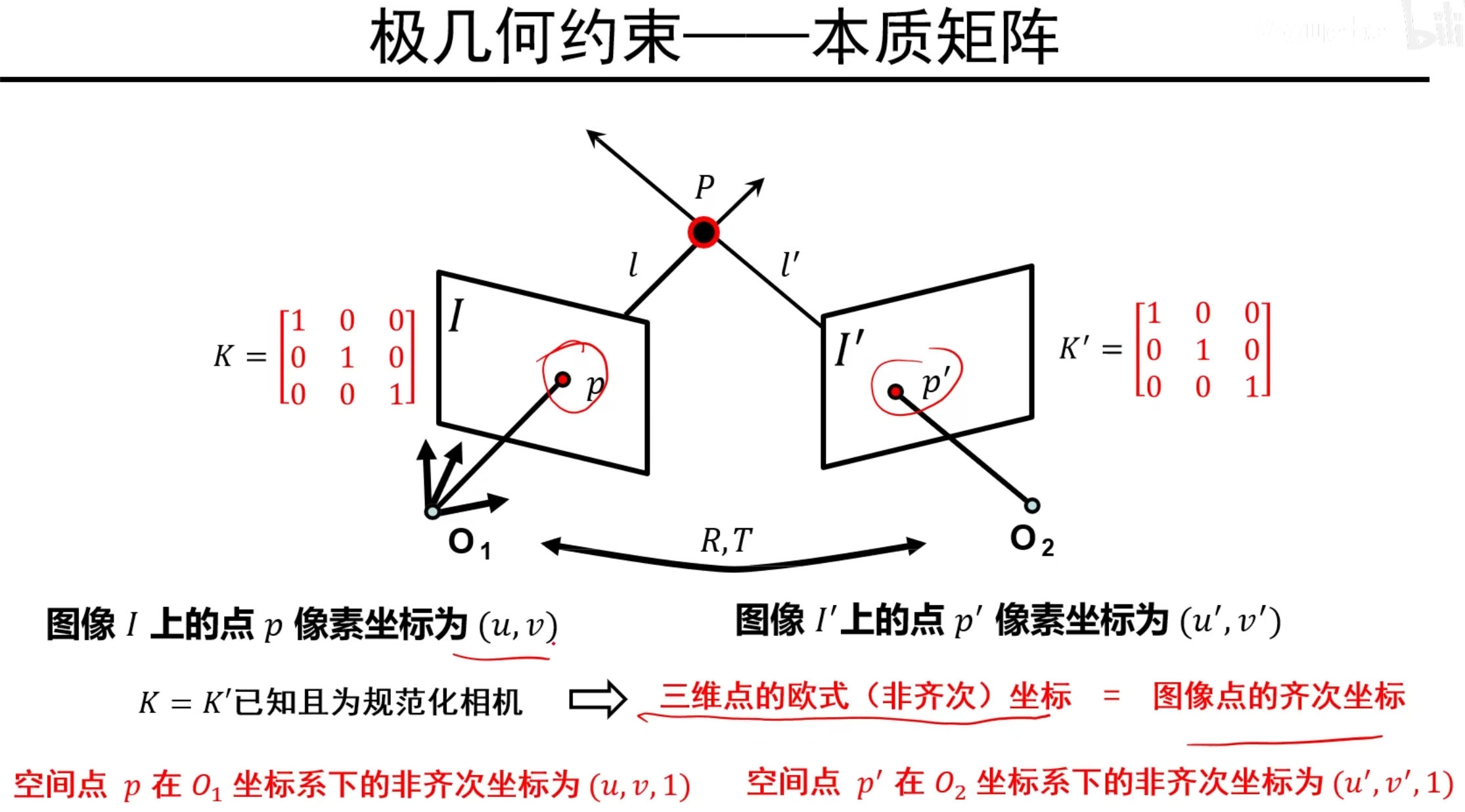
说明:因为是规范化相机,所以从二维空间反得三维空间坐标,其实就是加上了一维1而已(因为M是类单位阵的特点)
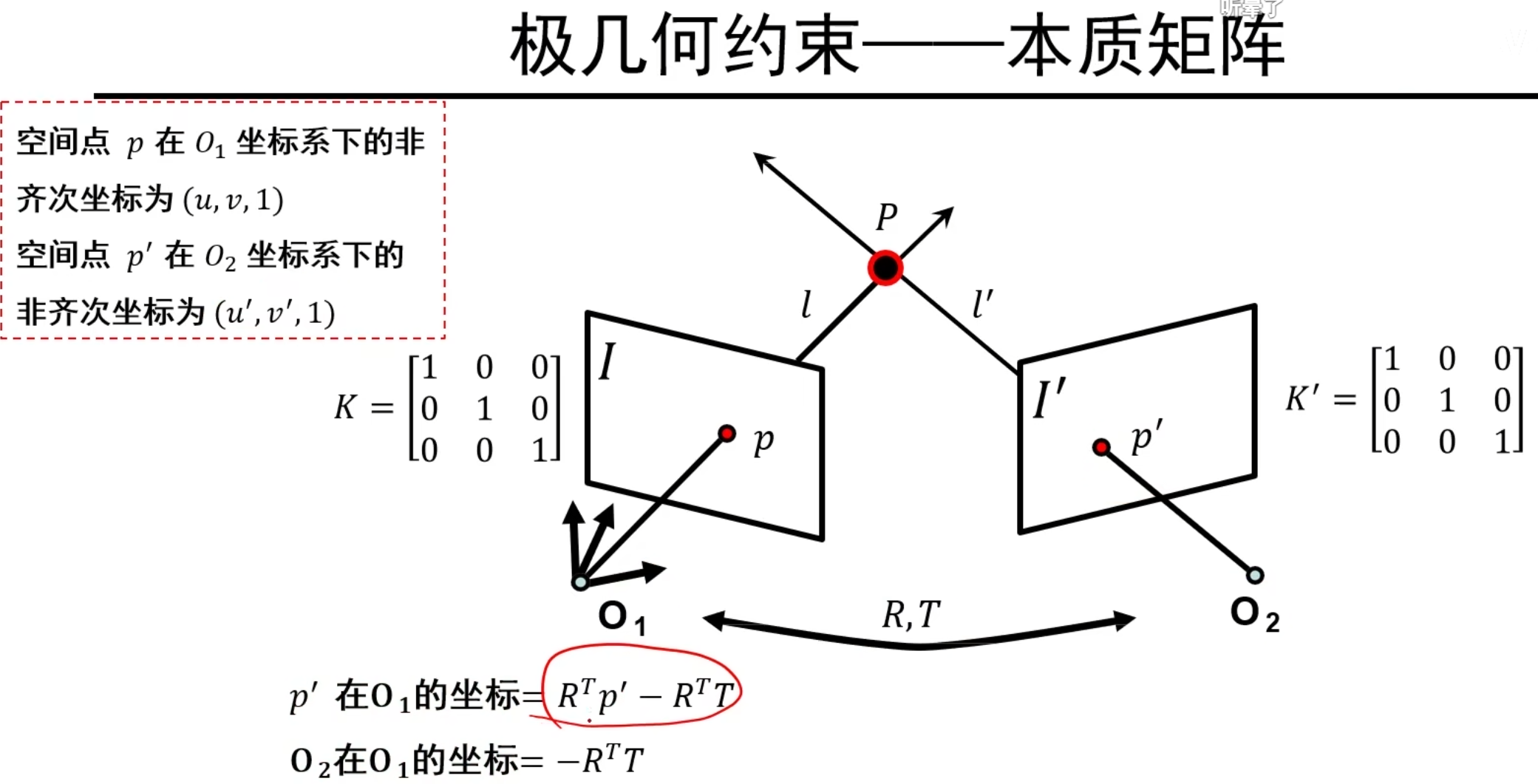
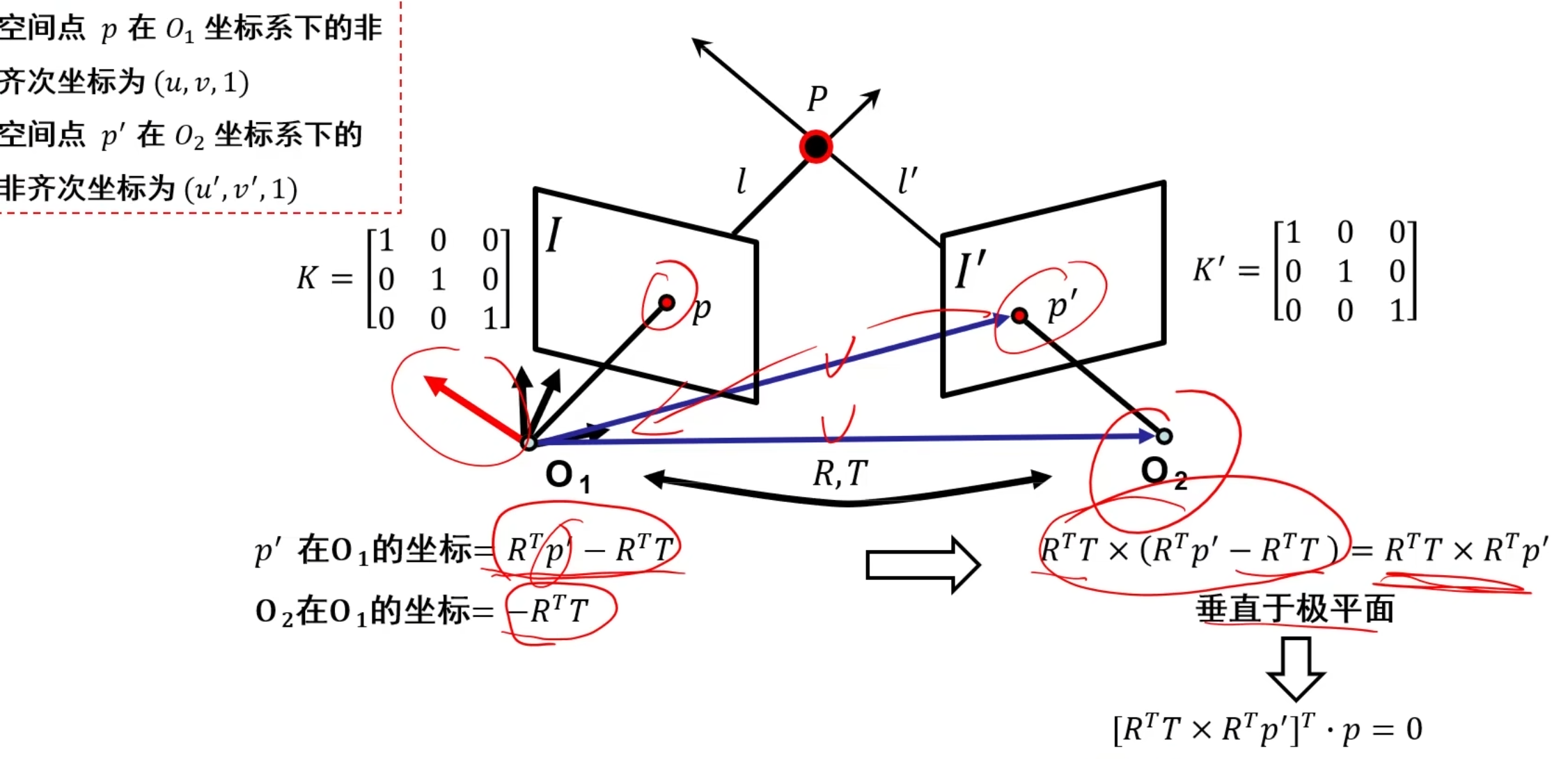
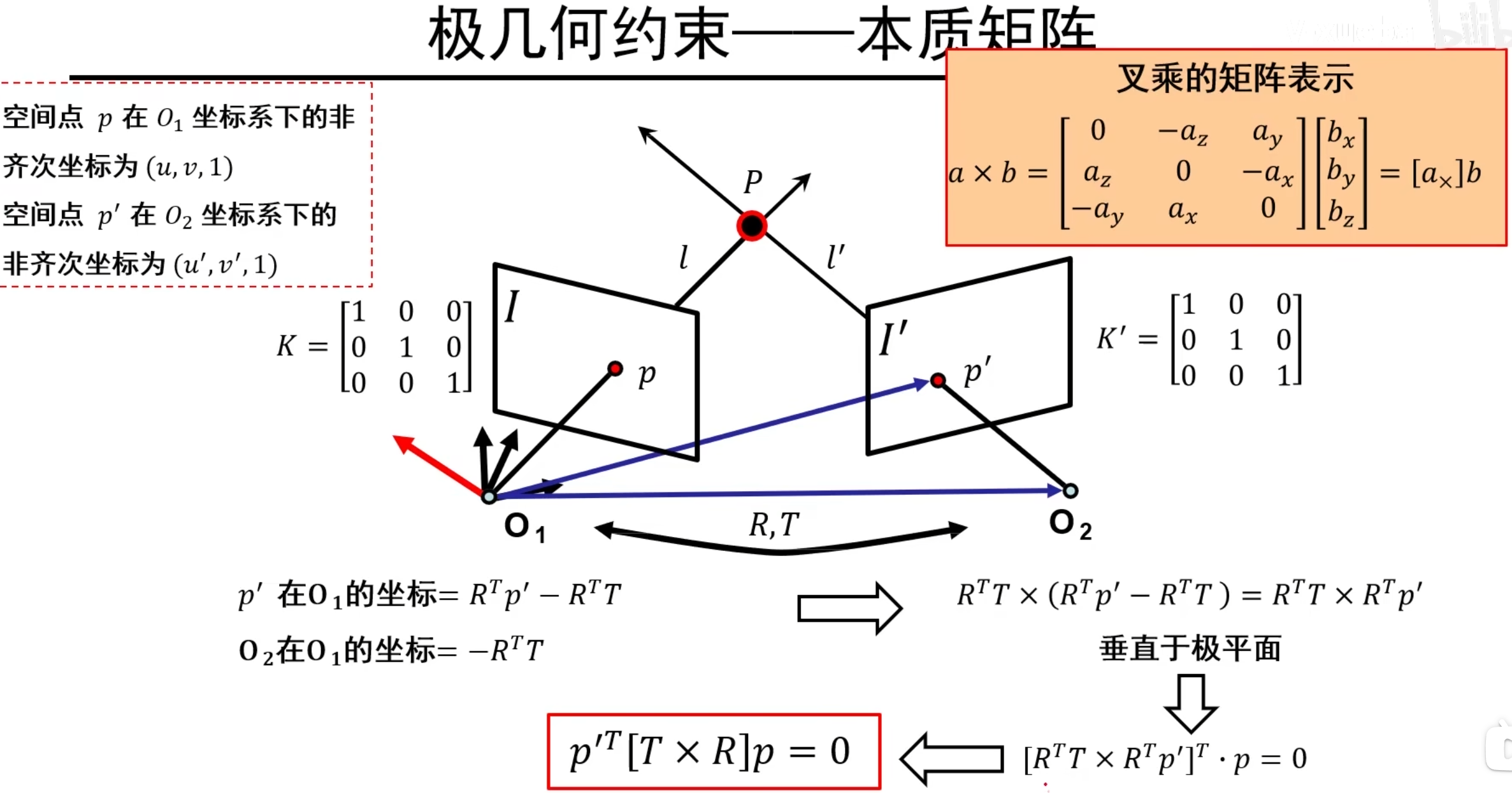
得到红色框框式子,我们就可以很清楚地看到p’和p的联系!
注意R,T是O~1~到O~2~的坐标系变换
于是,我们得到了本质矩阵,即规范化摄像机下两个像点之间的关系的代数表示

本质矩阵推出的性质
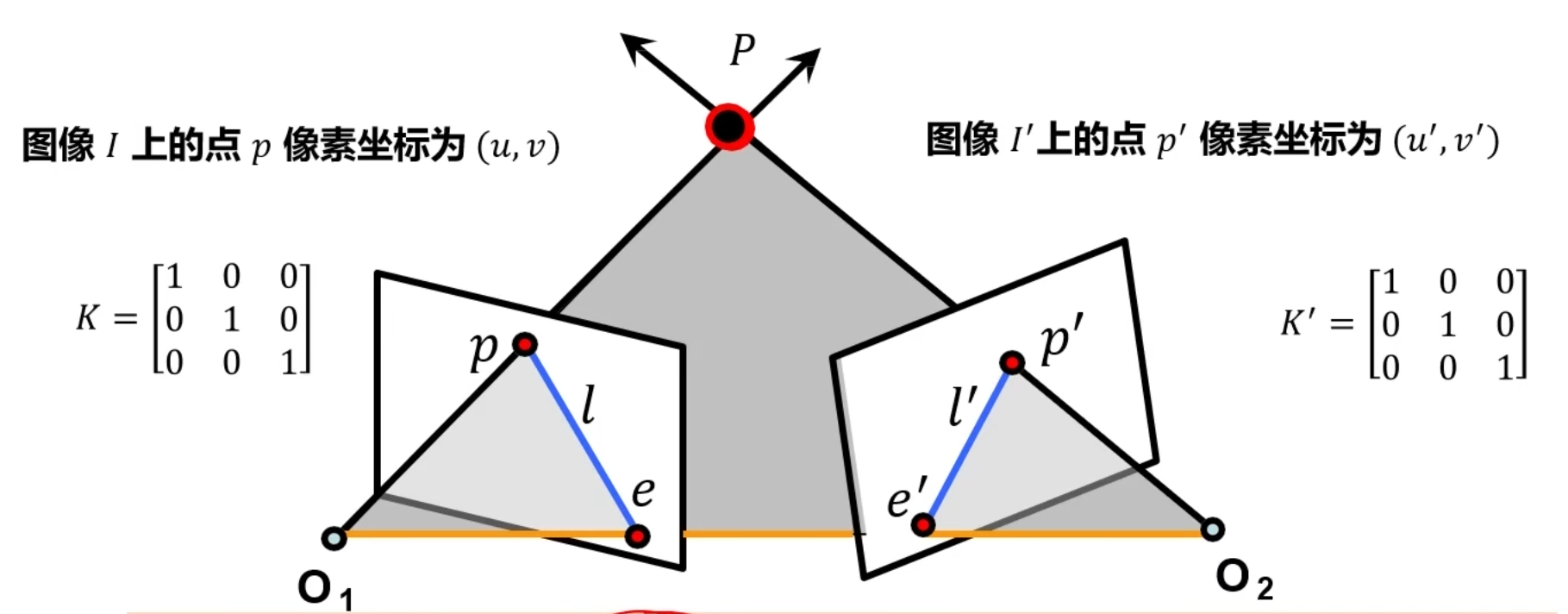
基础矩阵
本质矩阵在规范化摄像机下得到了两点极几何关系,为了得到更一般的关系,我们来讨论基础矩阵
基础矩阵对一般的透视摄像机拍摄的两个视点的图像间的极几何关系进行代数描述
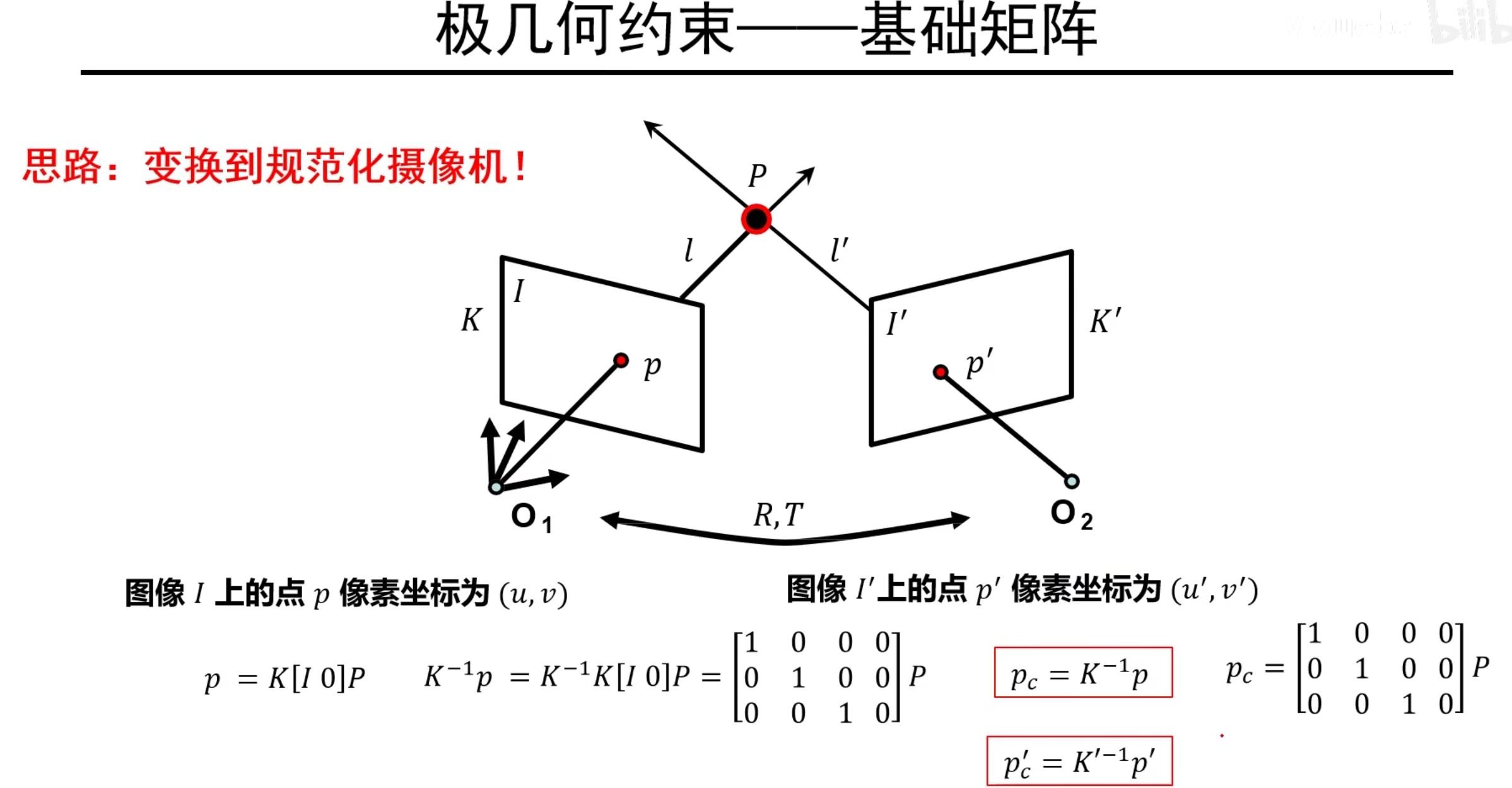
现在,就是K不再是规范化摄像机矩阵,那么,我们的思路就是把K变到规范化摄像机下,再运用本质矩阵就可以了!
如图,p~c~就是规范化相机下的像素空间点了,那么就满足本质矩阵,代入如下:
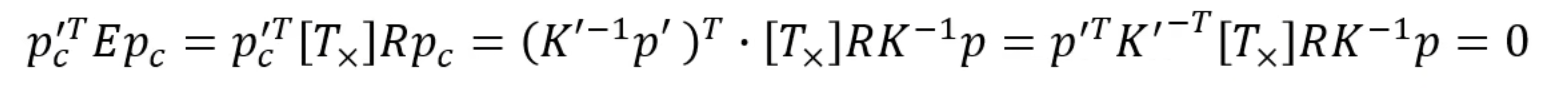
进行整理,我们就得到了基础矩阵!
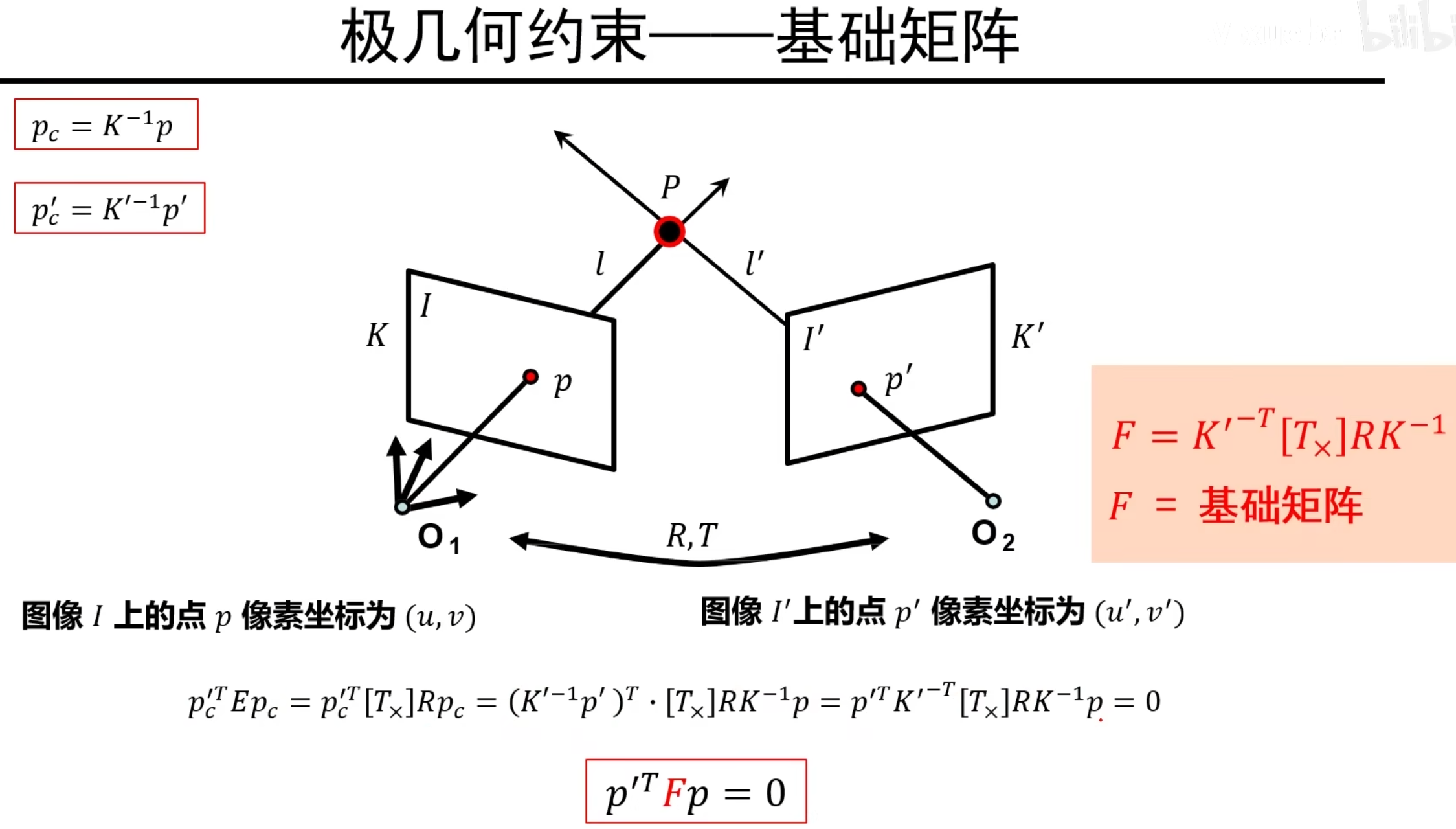
这样我们就得到了更一般摄像机下两点的极几何约束关系
基础矩阵推出的性质
基础矩阵估计
现在反过来思考,我们可以通过图像处理方法方便得到视点的对应关系,但是两个摄像机的内外参数不好确定,所以我们想要同一种方法,通过已知的极几何对应关系,估计出基础矩阵F,进而得到摄像机的内外参数
八点算法
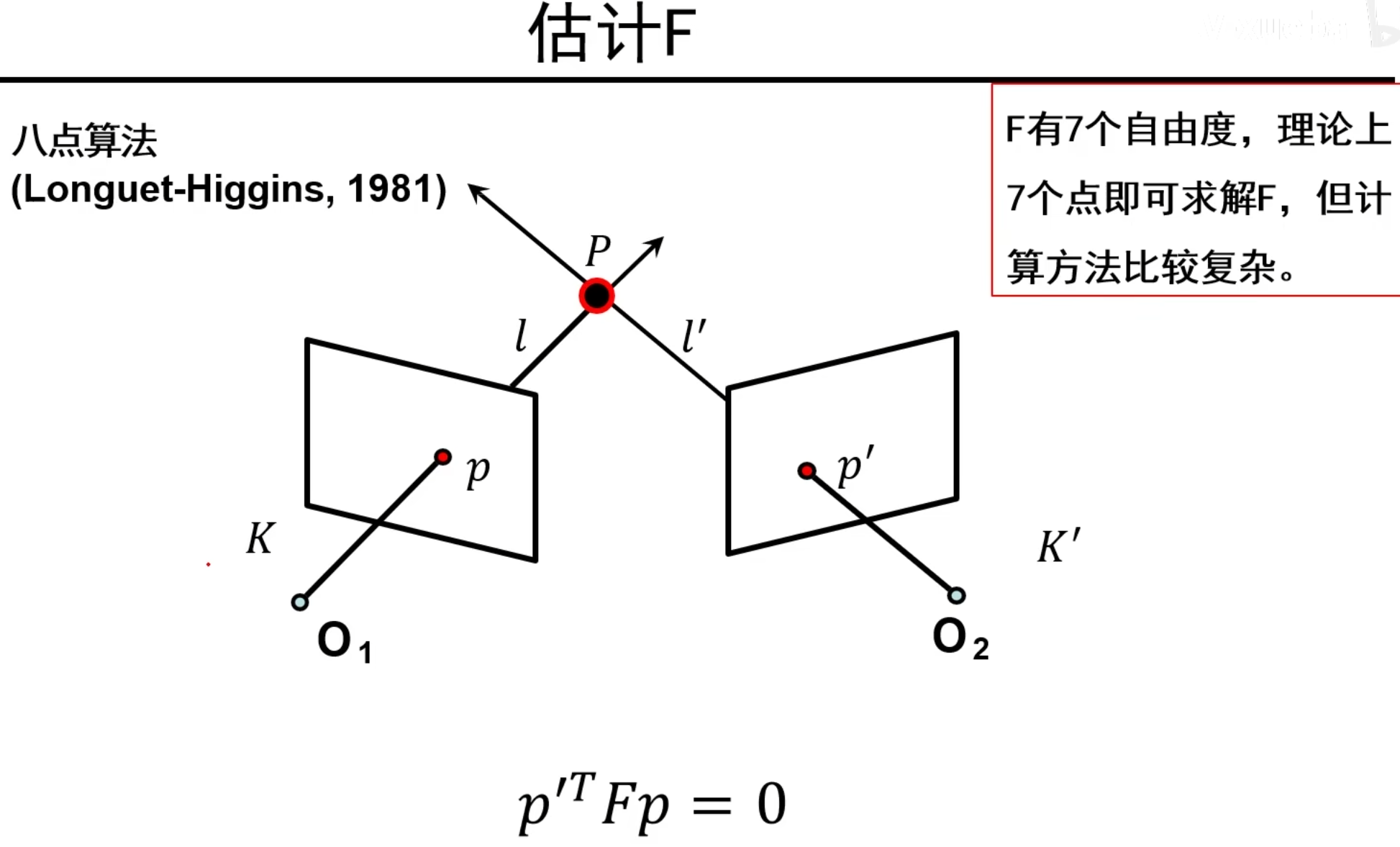

说明:进行如上图改写后,可以发现,一对点p,p’只能提供一个方程,所以我们需要八对点,(因为七对不好求)
比如下面同颜色点为一对点
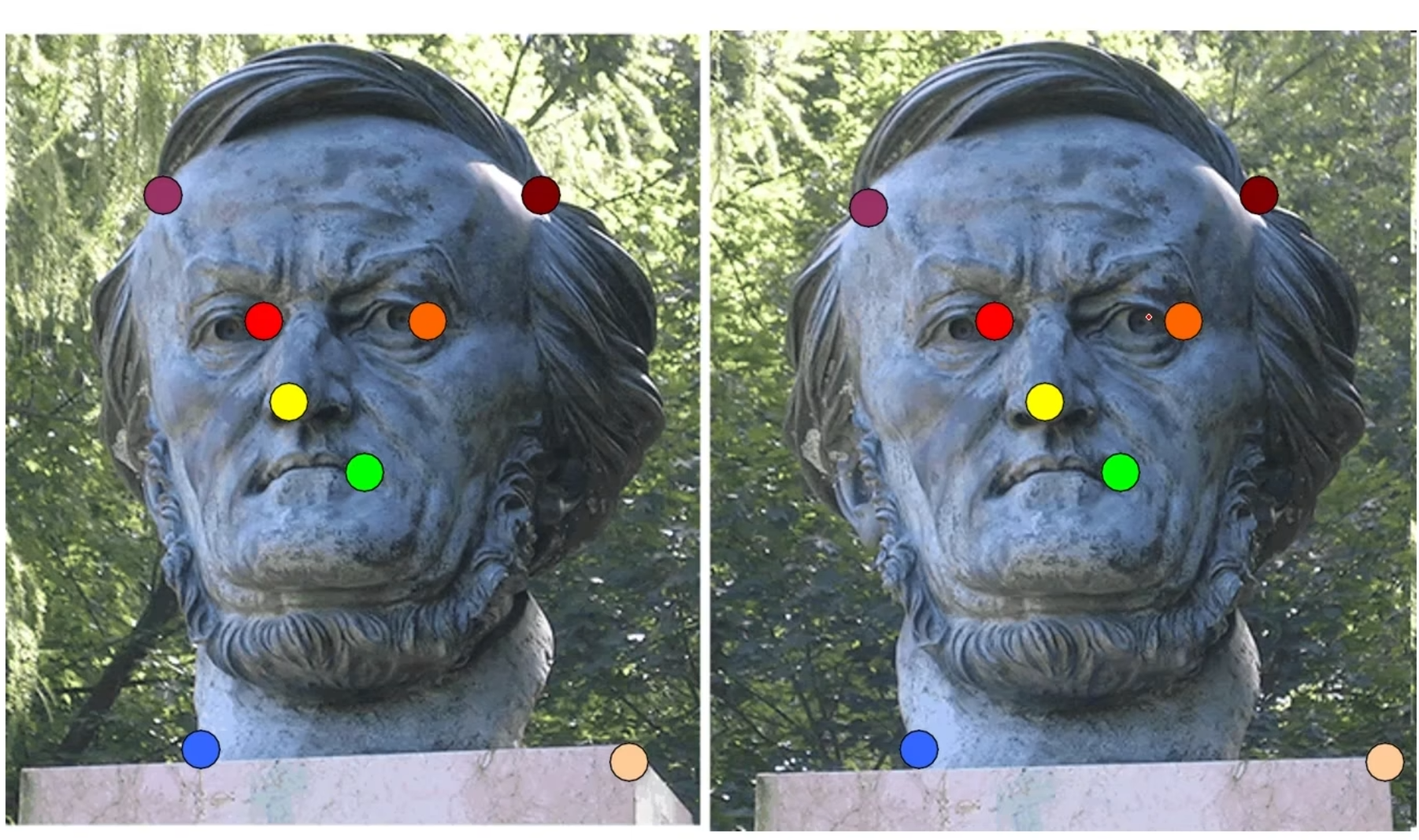
选取八对点后,就可以列出下图的方程:

可以发现这是一个齐次线性方程组最小二乘解问题,奇异值分解即可
f就为W矩阵最小奇异值的右奇异向量,且f的模为1(约束)

说明:红色框是进一步优化的要求,det(F)=0使得秩为2,左边要让我们估计的F尖尽可能接近真实的基础矩阵F
相当于对估计得到的F再进行一次最小二乘,再用一次奇异值分解,把s3直接干成0!
(神秘…课上说这个结论,不要求掌握推导)
由此我们可以完整编程八点算法了:

八点算法的问题

数值精度,数值计算有问题,因此我们引出一个更好的方法——归一化八点算法
归一化八点算法

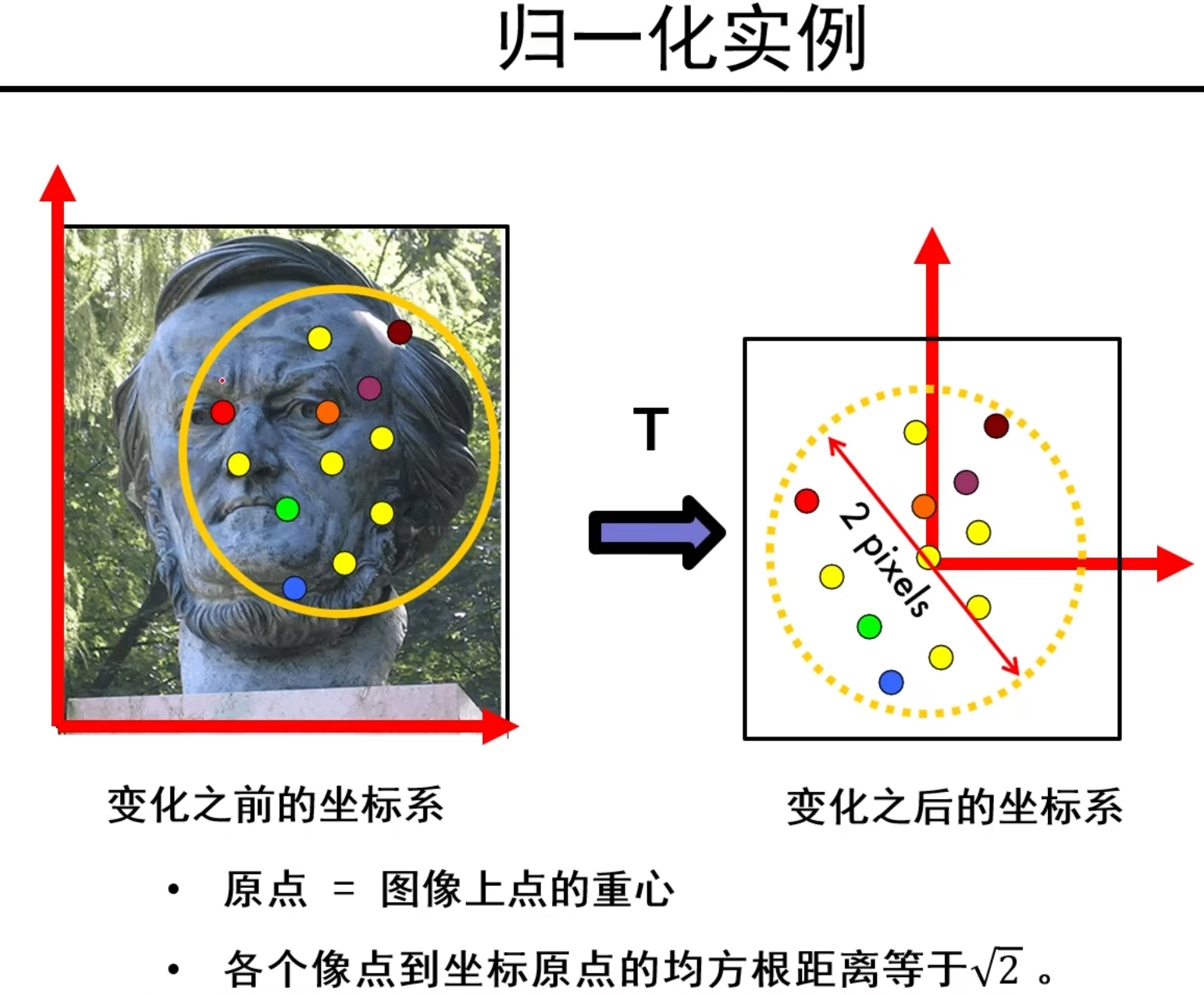
因此,我们得到归一化八点算法:

单应矩阵
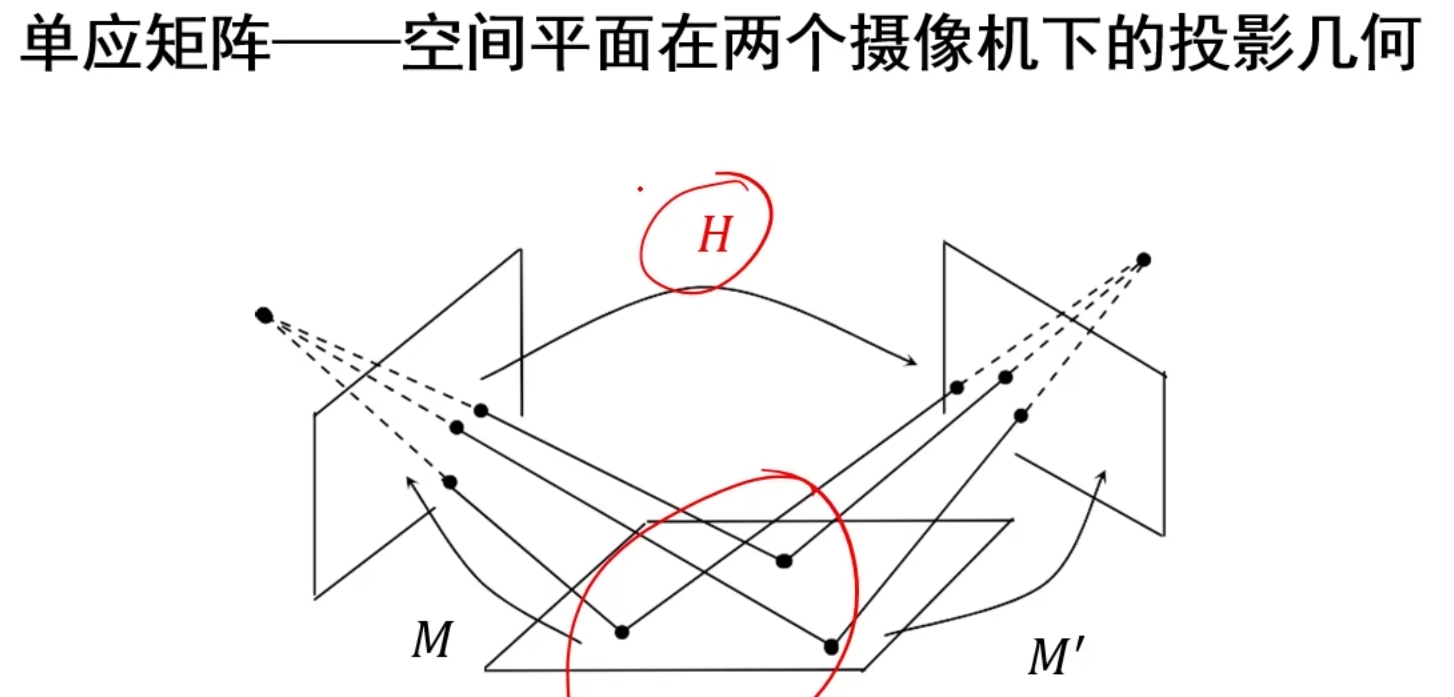
当我要找的视点在三维空间中实际上都位于同一平面上时,基础矩阵就很难估计出来了(在同一平面点有相关性,会导致退化)。因此我们单独提出一个单应矩阵来解决这个情况

上图推出了单应矩阵H
可以发现,之所以叫单应矩阵,因为现在p和p’的对应关系是一一对应了,而原来在本质矩阵和基础矩阵中,p是对应一条线,p’也是对应一条线的。
单应矩阵的估计
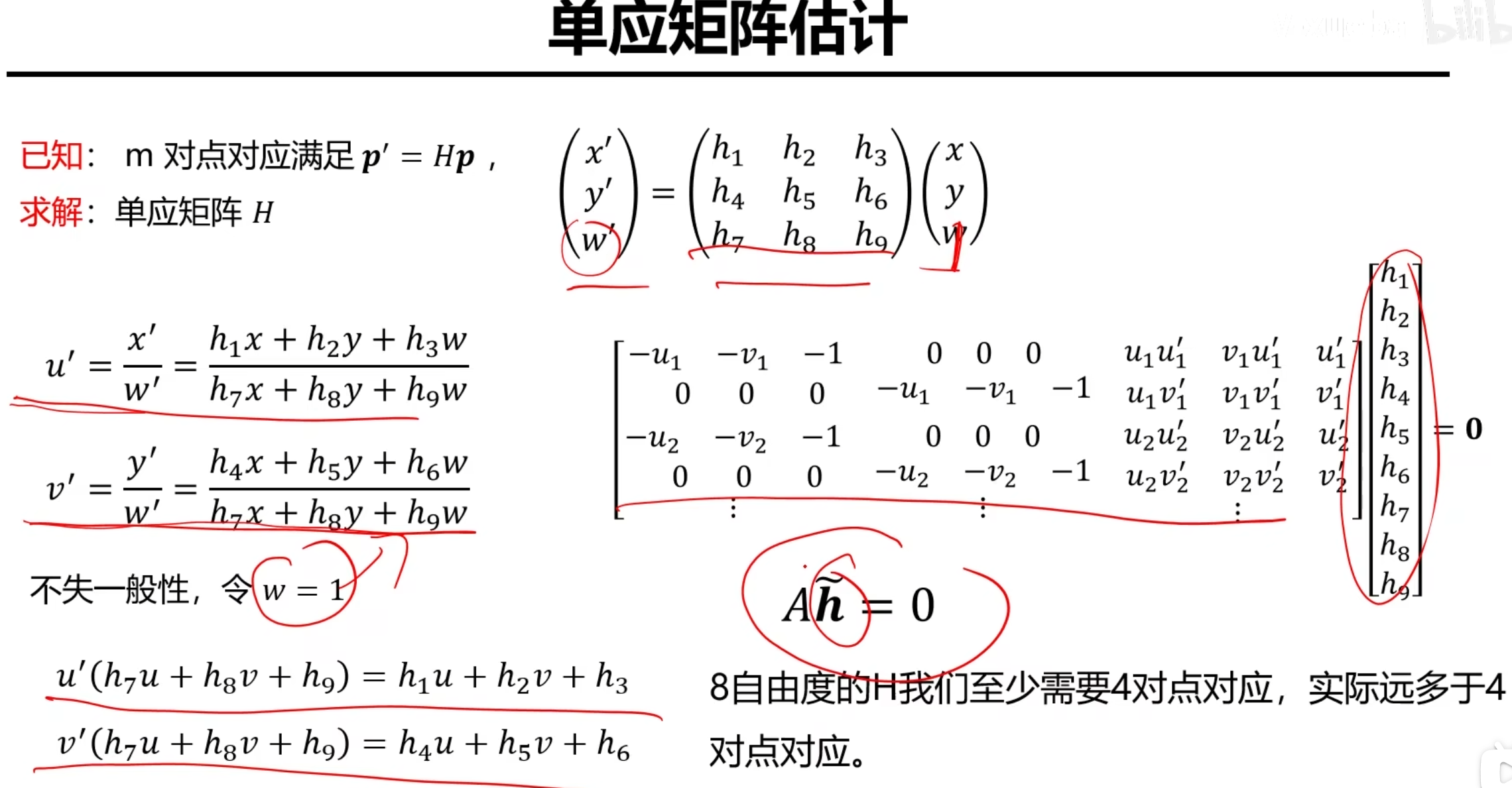
基本上同之前的没什么区别
单应矩阵的性质
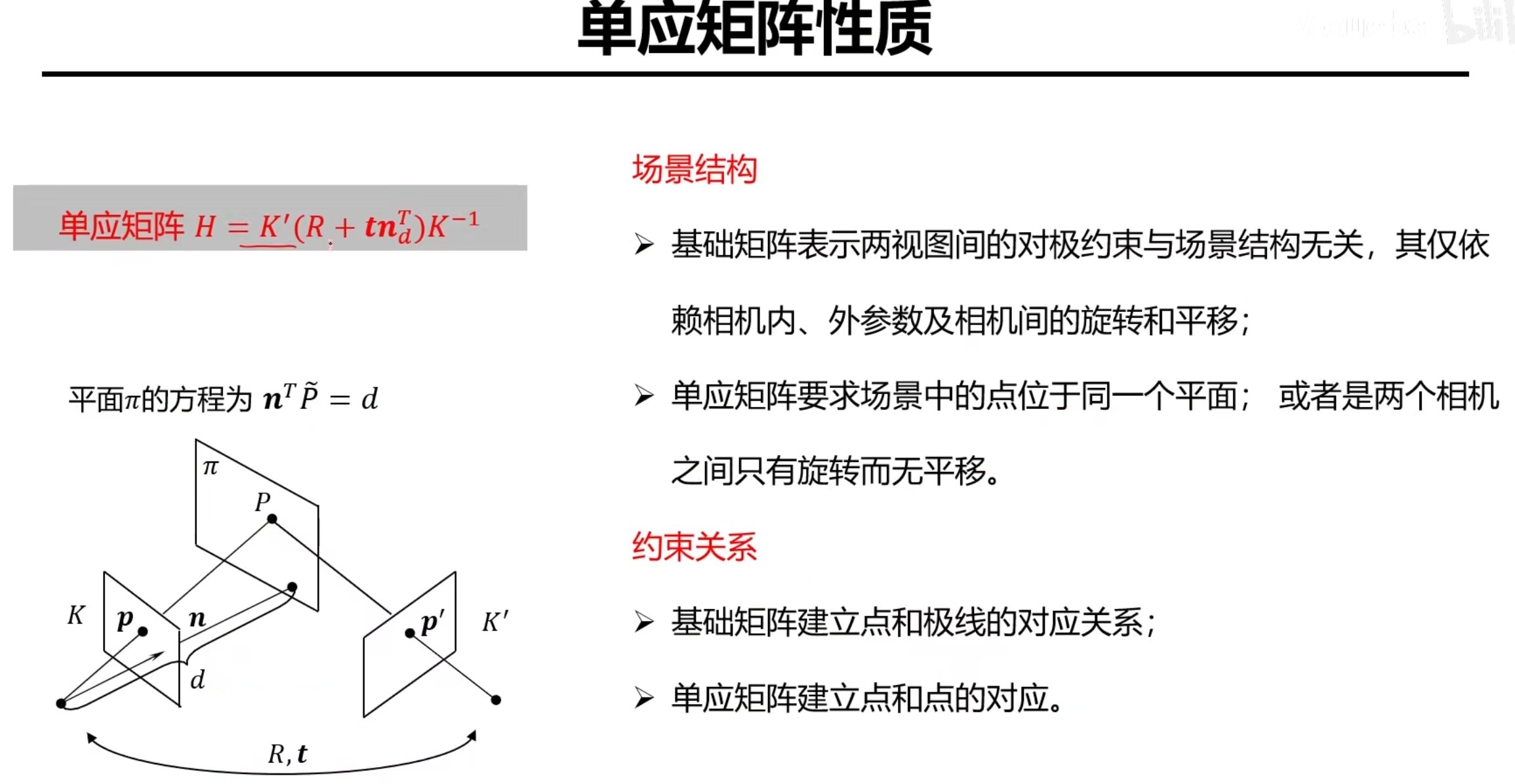
5.双目立体视觉
基于平行视图的双目立体视觉
基础矩阵F的新表达式
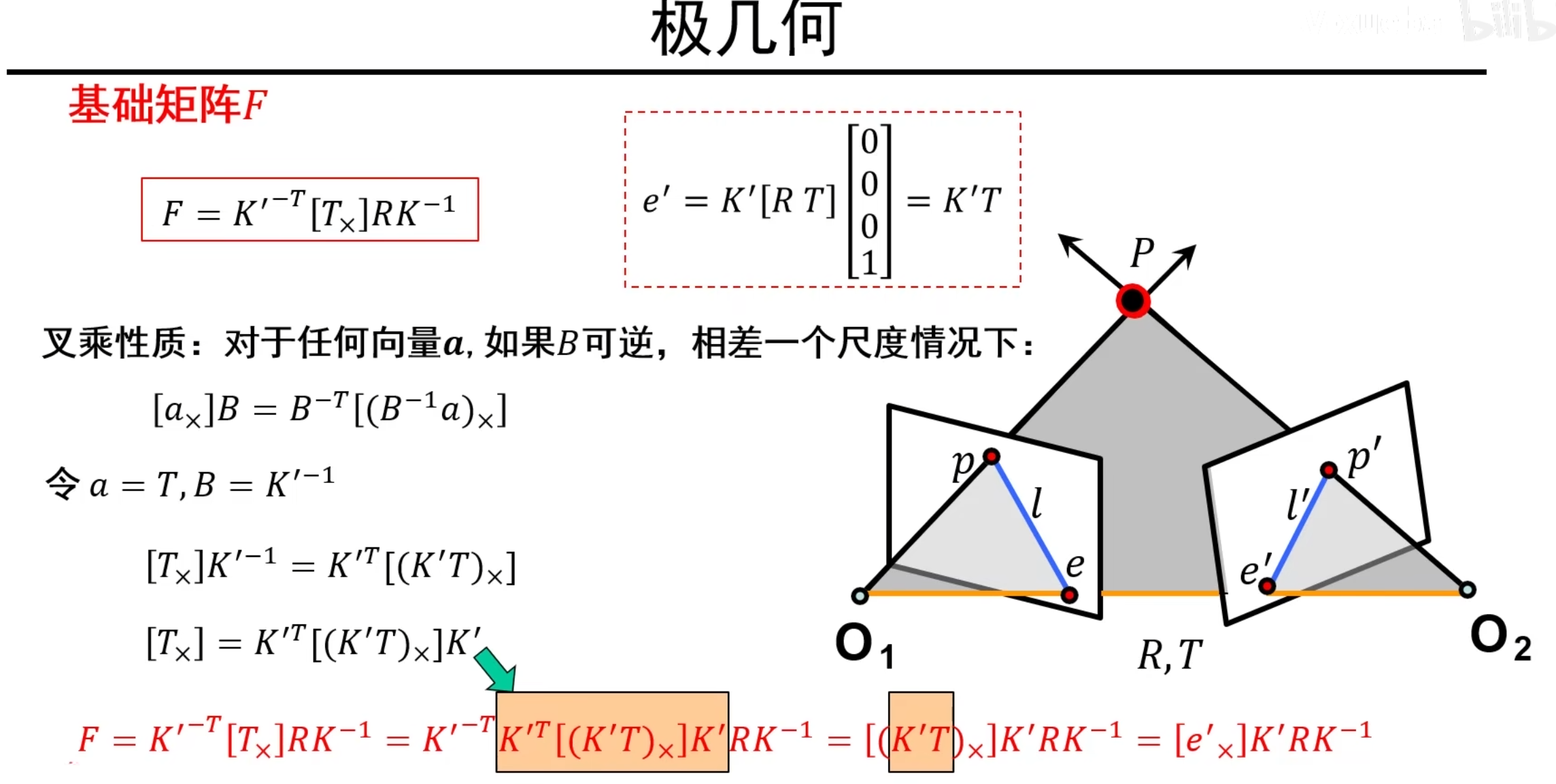
平行视图中的基础矩阵F
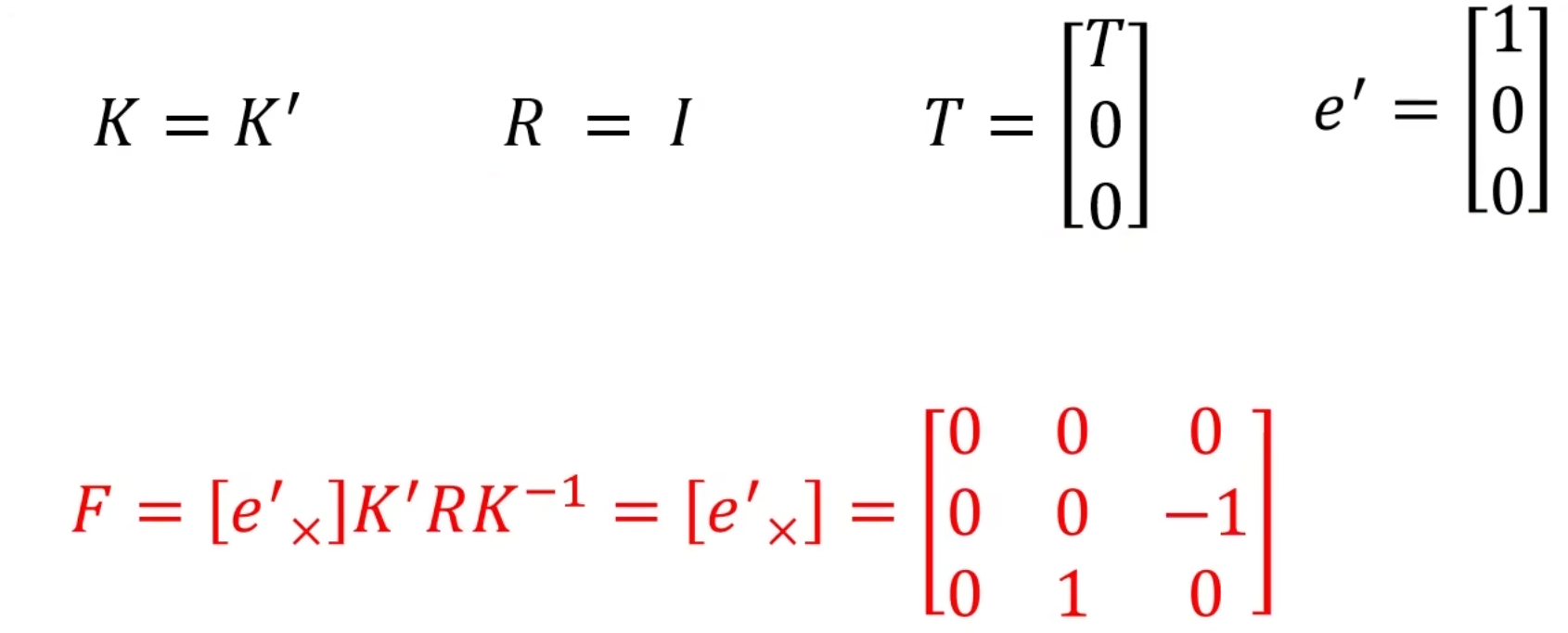
说明:无旋转,R=I,两个摄像机内参数矩阵相同,K=K’,e’点在三维空间中是一个无穷远点(因为平行视图中极点都平行于基线,也就是平行于u轴,而u轴的方向向量是[1,0],根据一条直线线对应的无穷远点就是其方向向量加一维0可得到极点的齐次坐标!)
因此,我们可以把基础矩阵F写成e’构成的矩阵!
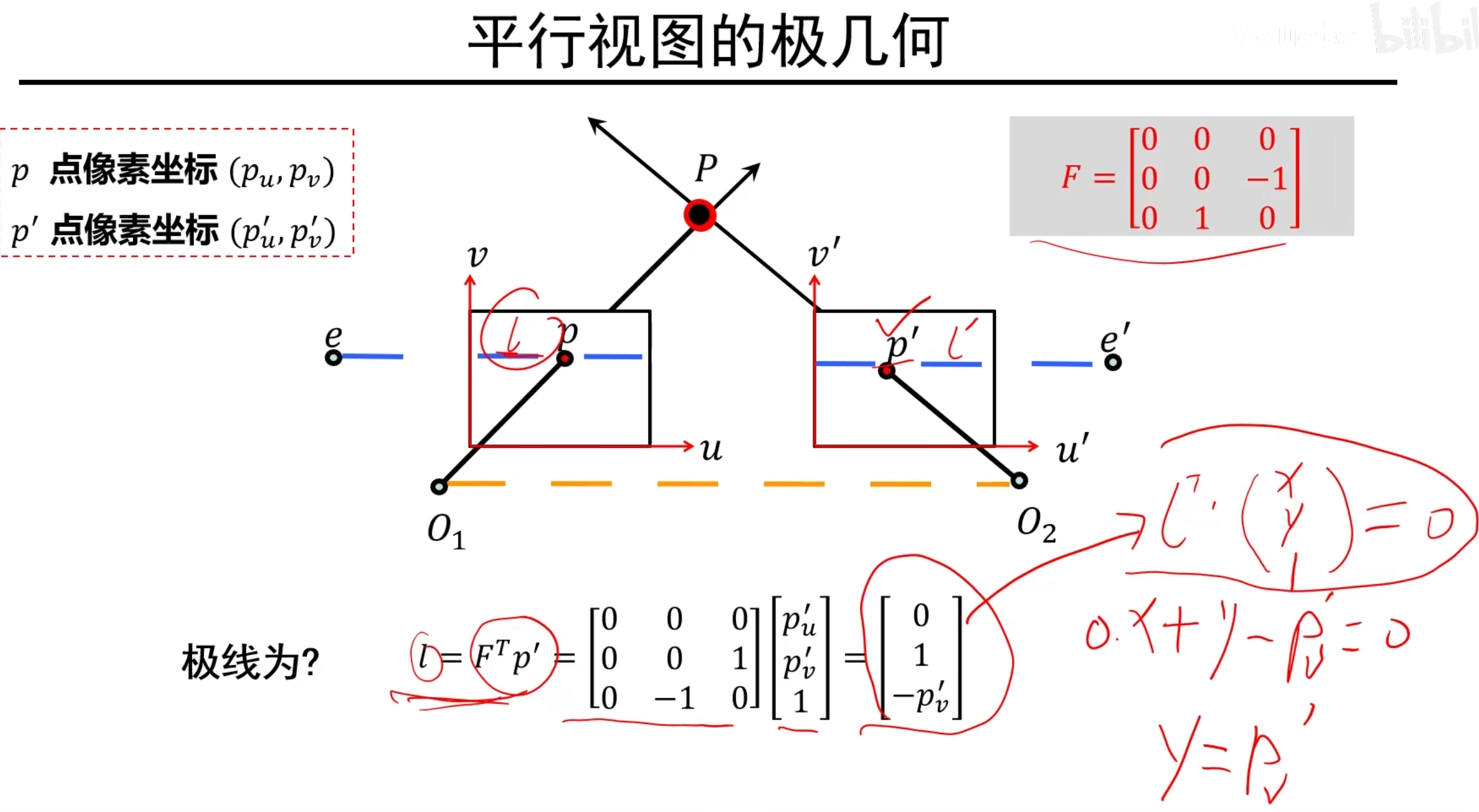
说明:可以根据上面简化过的F矩阵推出,极线是y=p’~v~的直线,也就证明了极线平行于基线!
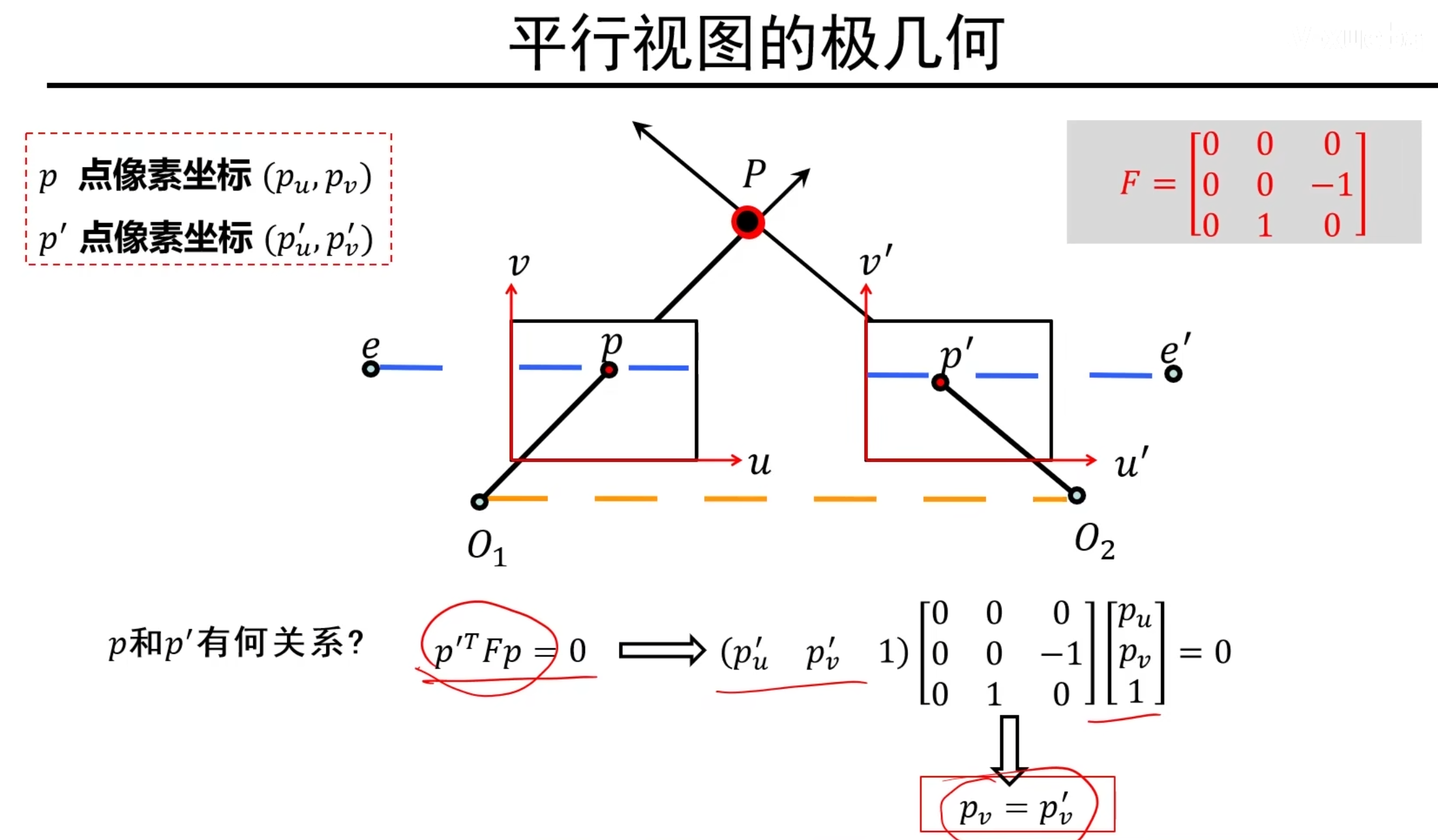

说明:进一步推出,一对对应同一三维空间点P的两个视点p,p’,在三维中是位于同一直线上的!
平行视图的三角测量
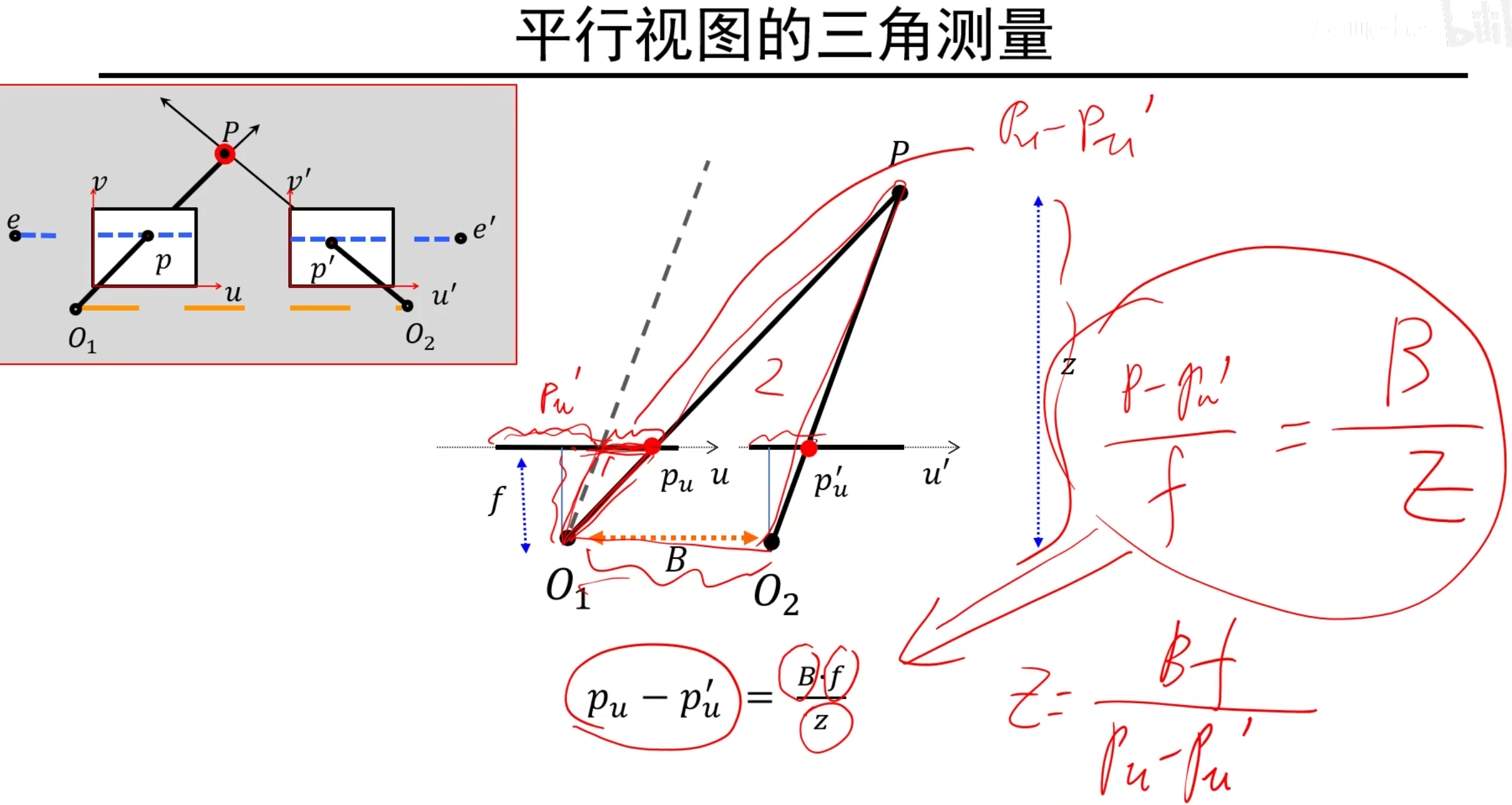
说明:中间图是左上角图的俯视角投影图,根据图中的相似三角形关系可以推出下面的黑色等式以及右下的红色等式
这就说明,我们现在不需要原来三角化中线性解和非线性解那么麻烦,而可以轻松根据这几个参数就可以得到一对视点对应的三维空间的点P的坐标位置!太好了!
视差图实例
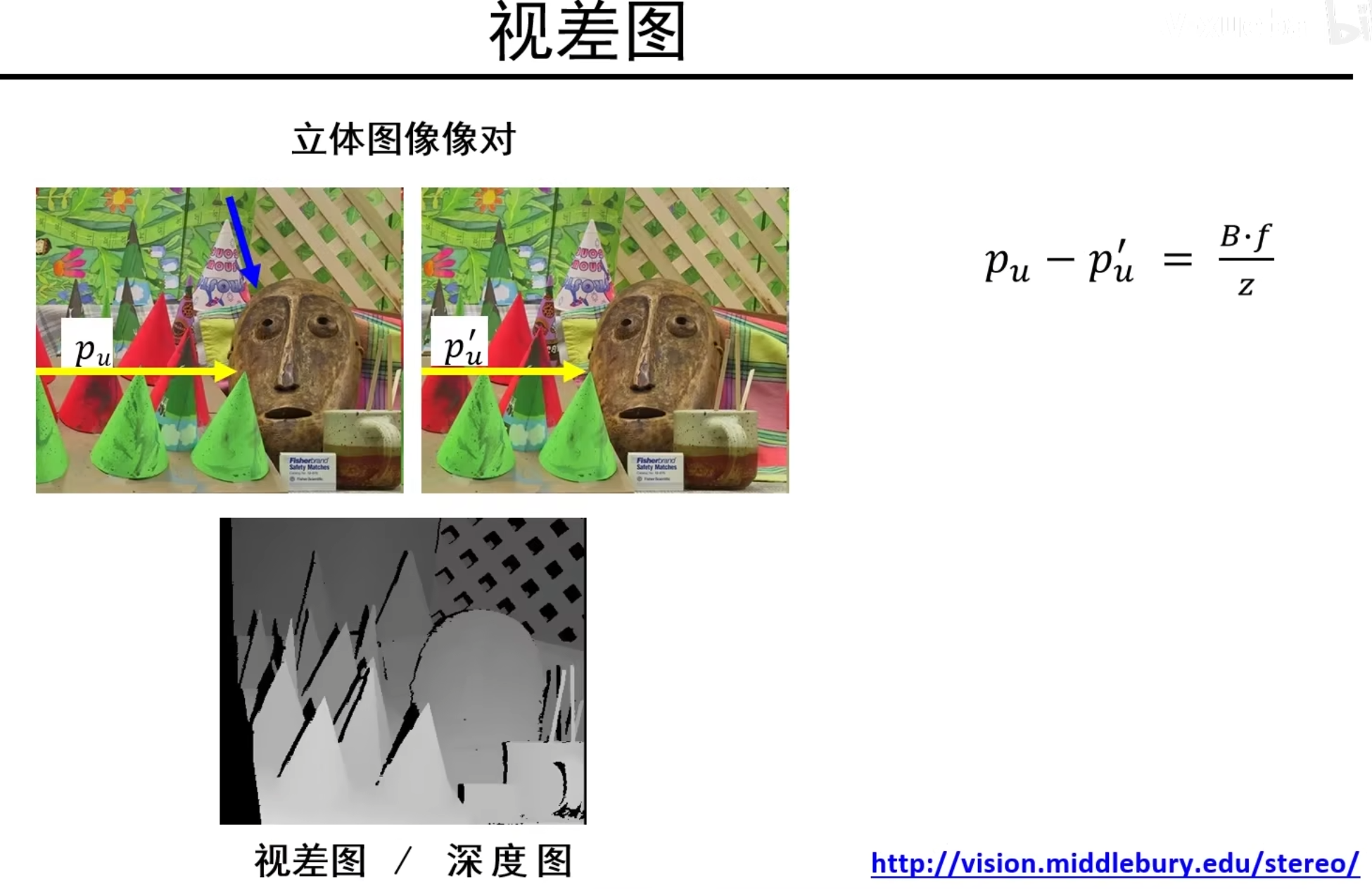
左上角两图是双目分别得到的两张图,上面取得对应的一对视点,可以得到下面的视差图
也就是说,可以实时算出一个点距离双目系统的深度
视差原理应用

说明:如第三张图的拳头,我们要让拳头感受起来靠近我们,就让拳头的视差变大,进而会使得其深度变小,感觉就靠近我们。
双目立体视觉系统的问题
1.我们如何构建平行视图?需要构建平行视图才能运用上面的结论
2.如何建立p,p’对应关系?
先关注第一个问题,我们进入本节课第二环节——图像校正部分!
图像校正
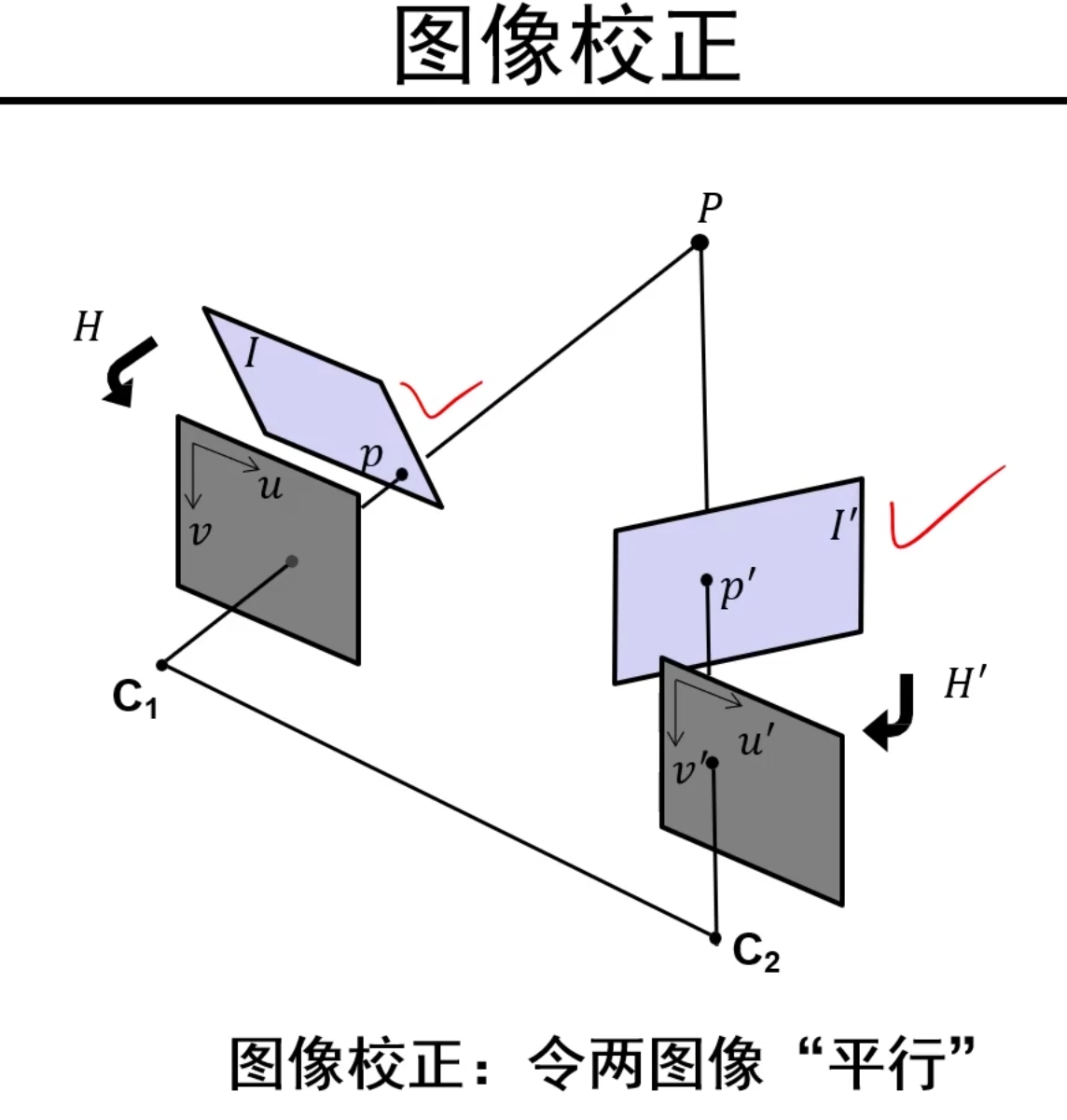
我们要做的就是找到两个变换矩阵H,H’使得两个像素平面变换成平行视图
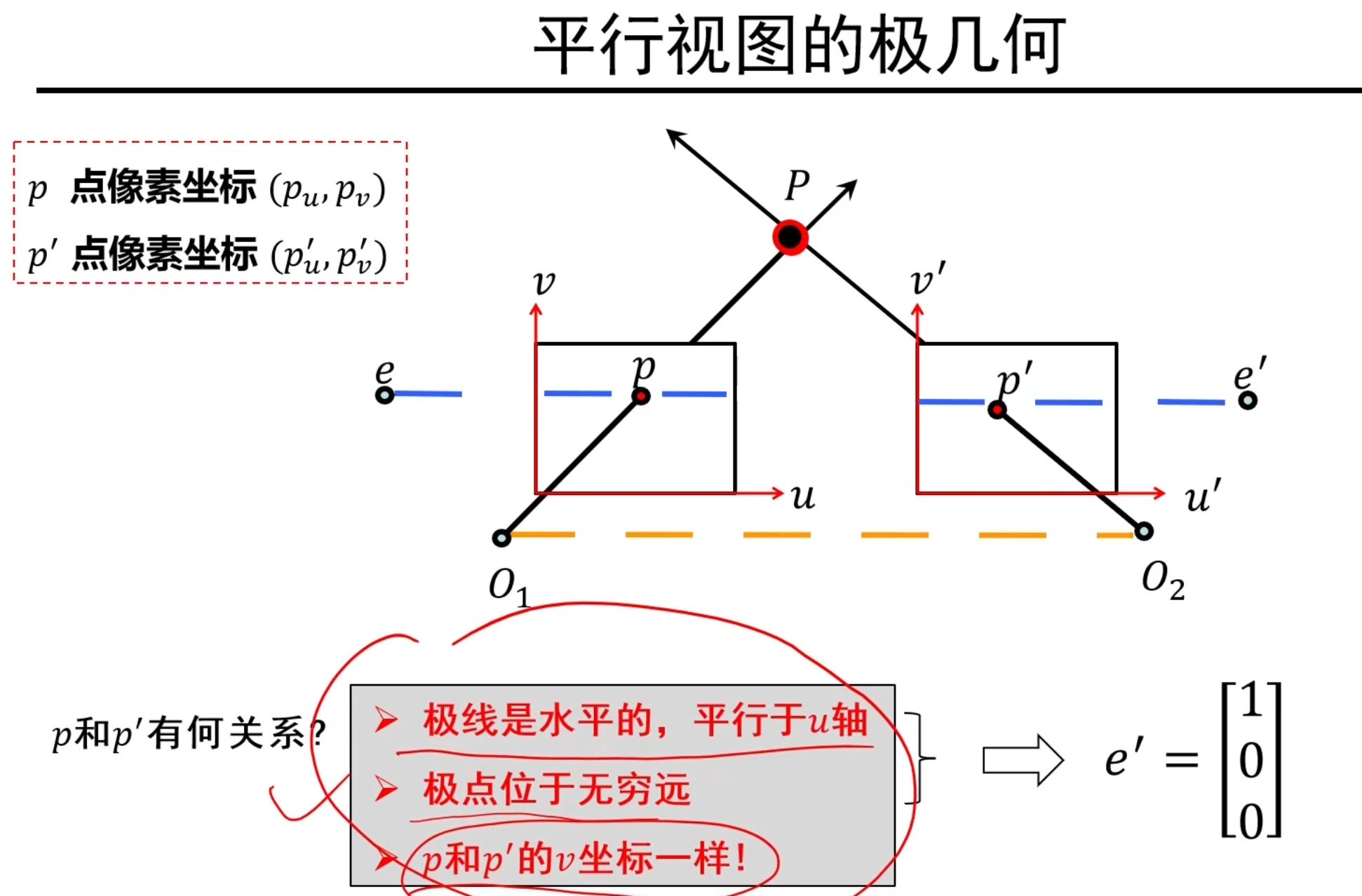
说明:要是平行视图,其实就是要满足极点齐次坐标为(1,0,0)即可!
图像校正的一二步

说明:使用八点算法计算基础矩阵F,通过基础矩阵的性质算出极线,因为所有极线都过极点,所以可以得到右边的齐次线性方程组,使用最小二乘法可以解得极点e和e’
图像校正的第三步
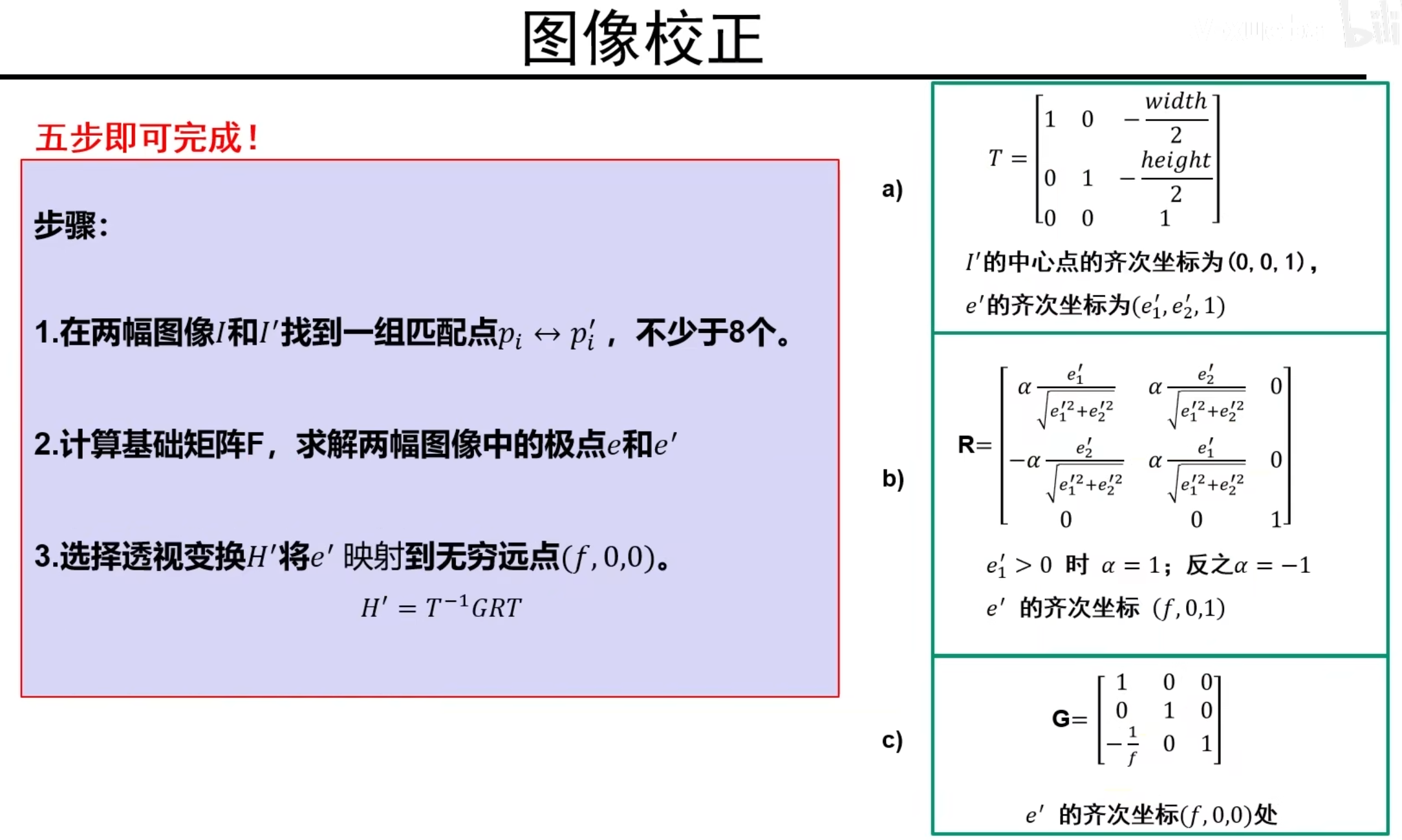
说明:第三步我们这里只对右图I’进行操作,找到使得I’变为平行视图的变换矩阵H’
a):先把图像的坐标原点从左下角移动到图像中心,那么极点坐标会跟着改变,改变完后的极点坐标为(e’~1~,e’~2~,1)
b):根据变换后的极点坐标构造一个旋转矩阵R如上图(没讲为什么),然后把极点乘以这个R旋转矩阵得到新的极点坐标
c):拿新的极点坐标构建一个G矩阵,再让极点乘以G矩阵,最后极点变化到(f,0,0),现在可以发现,极点坐标已经是一个无穷远点的坐标了!
但是这里我们是原点在图像中心下得到的,我们还要再把原点移回图像左下角,因此需要运用一个T^-1^逆变换,也就是紫色框框中最下面的变换矩阵H’中的T^-1^的原因
图像校正的四五步

说明:第四步是个结论,找到一个H使得Hp~i~和H’p’~i~的距离最小,这个H就是我们要求的左图I的变换矩阵H
最后,第五步中让左右图都进行变换得到平行视图
图像校正的示例

对应点搜索
我们如何找到一对视点,也就是说给定一个p,我们如何找到p’,给定p’,如何找到p
原来单视图中,要找到对应点,根据极几何知识,我们需要先找到对应的极线,再找极点。
现在我们关注于双目平行视图,因此对于一个点p,只需要沿着水平线找p’即可。
对于平行视图找对应点,我们使用相关法
相关法
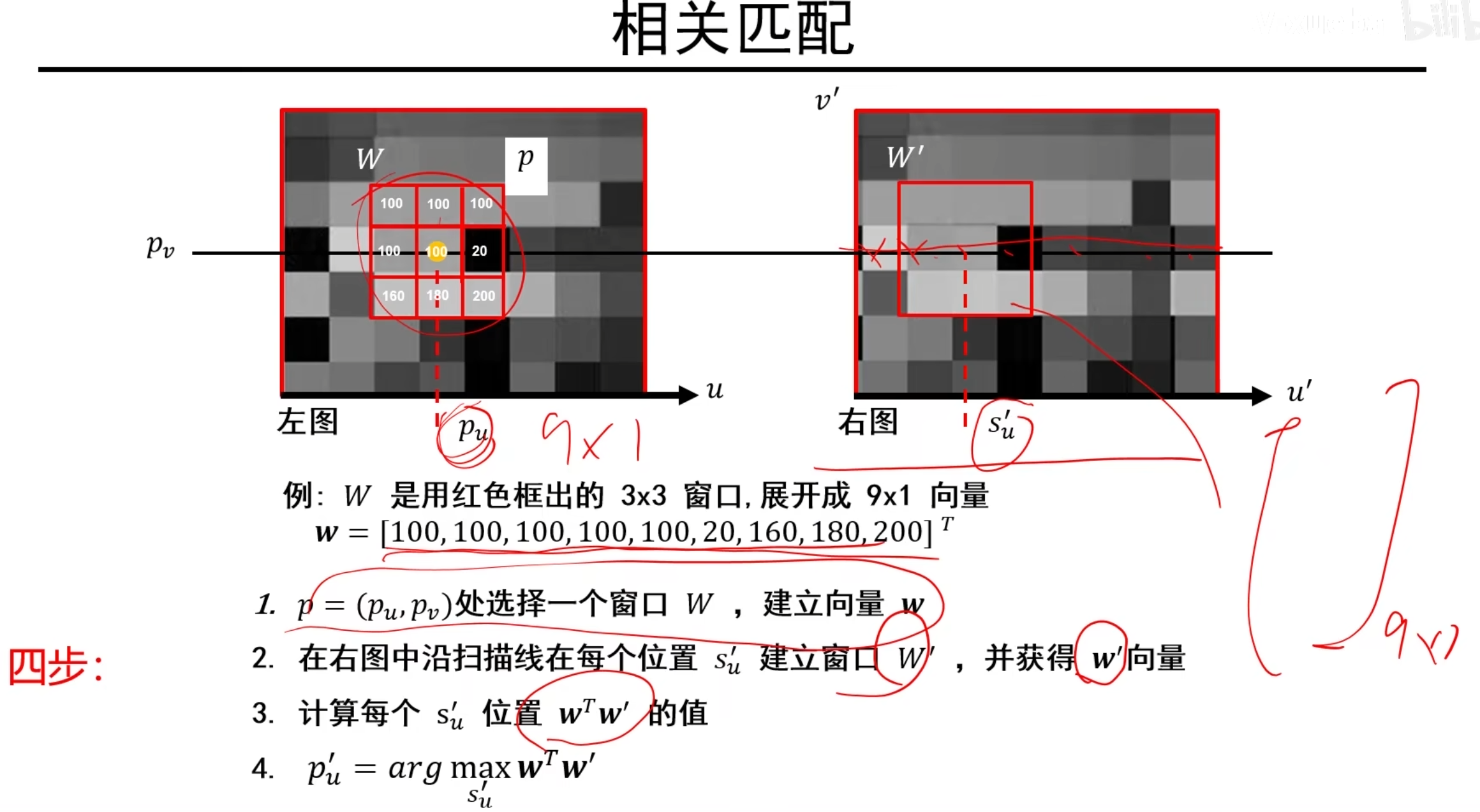
说明:每个像素中的值为其灰度值
右图中每一个u坐标都取出一个矩阵w’,让w点乘w;,则p’就是使得点乘值最大的那个u坐标
w^T^w′=∥w∥∥w′∥cosθ,当 cosθ越接近 1 时,说明两个向量的方向越接近,也就是说 w和w′ 越相似,点乘越大,表示两个窗口的像素分布越接近,即对应的灰度模式更加相似。
朴素相关法算法的问题

当两张图亮度不同时,会导致灰度值差异很大,因为灰度值和亮度一样是RGB使用一个特定方式加权平均得到的。
因此,我们需要改进一下算法,使用归一化相关匹配。
归一化相关匹配
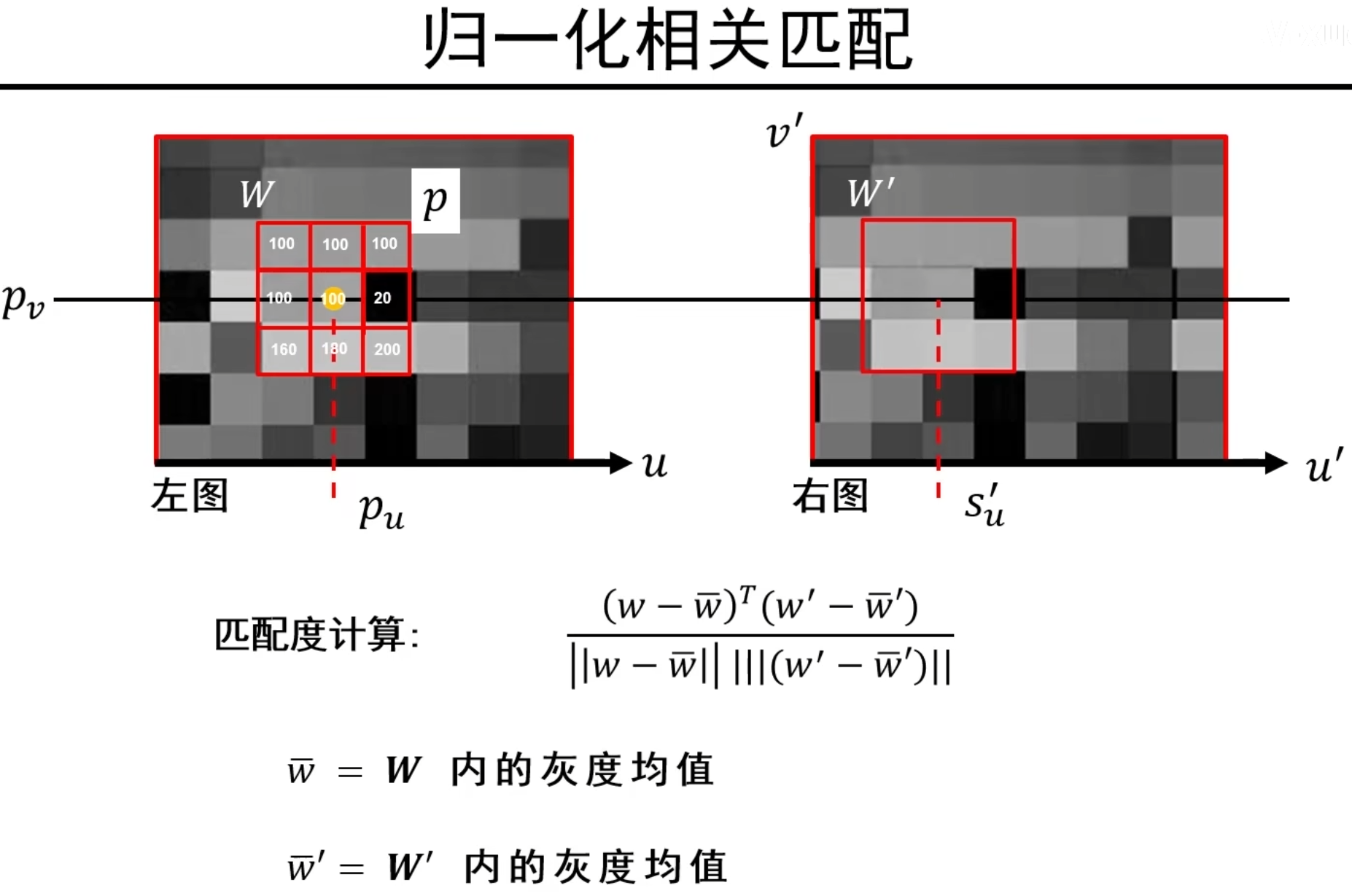
说明:再计算点乘之前,w先减去w九格像素内灰度值的均值,w’同理。原因是不同图像区域可能有不同的亮度(整体灰度值偏高或偏低),但亮度的绝对值不一定能反映特征的本质。减去均值后,灰度值被中心化,表示每个像素相对于该窗口的平均灰度值的偏差,突出灰度的相对变化,而不是绝对大小。
归一化后的点乘计算(即余弦相似度)实际上在衡量的是两个向量的方向相似性,而不是它们的绝对值大小。这样,比较的是图像窗口内的灰度变化模式,而非整体的亮度或对比度。值范围在 -1 到 1 之间,值越接近 1,表示两个窗口在灰度分布上的相似性越强;值越接近 -1,表示两个窗口的灰度分布相反。
归一化相关匹配算法如下:
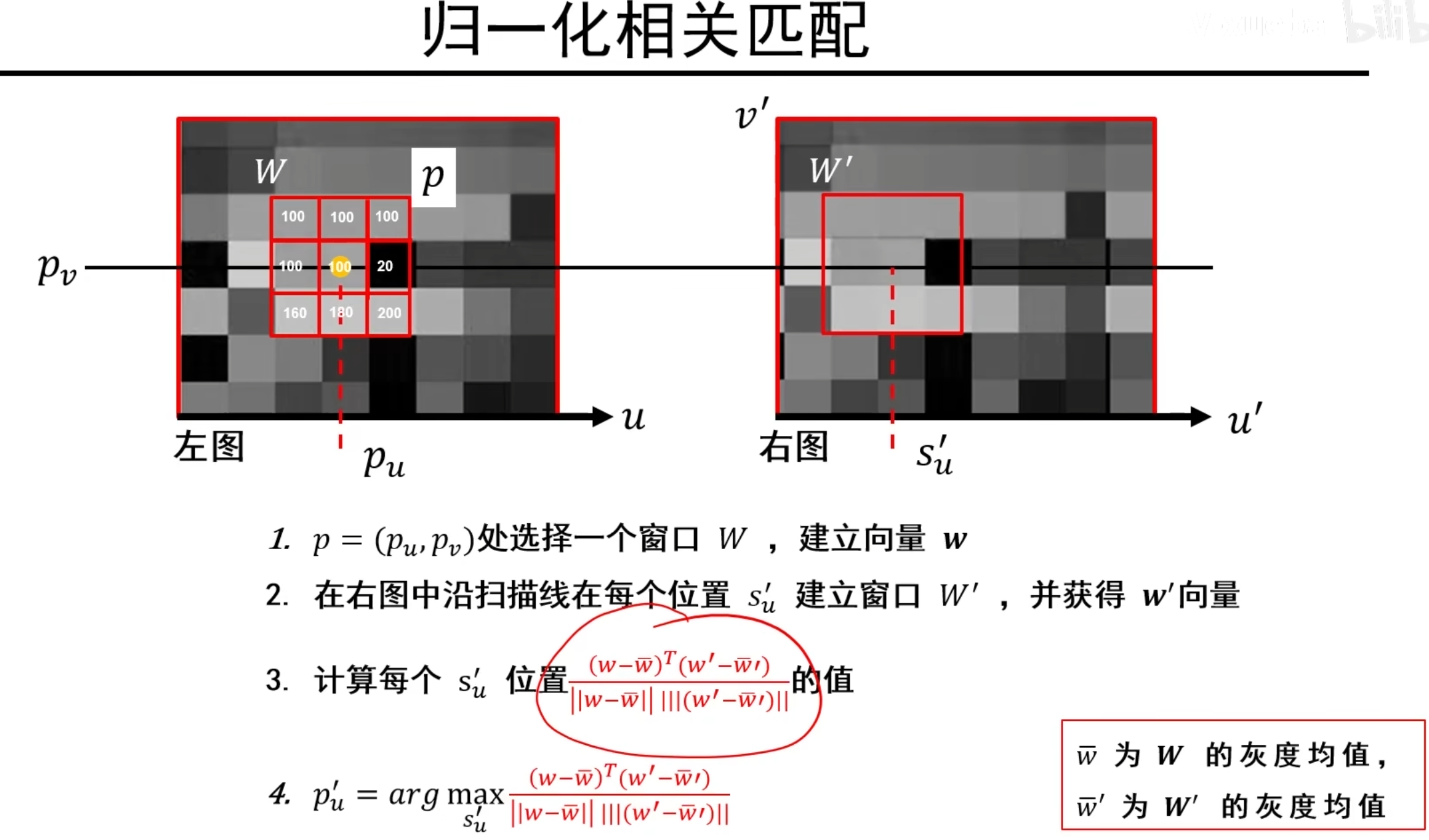
窗口大小的影响

说明:可见,窗口大小是一个经验参数,而且不能两全
更好的方法——Graph cuts图割法
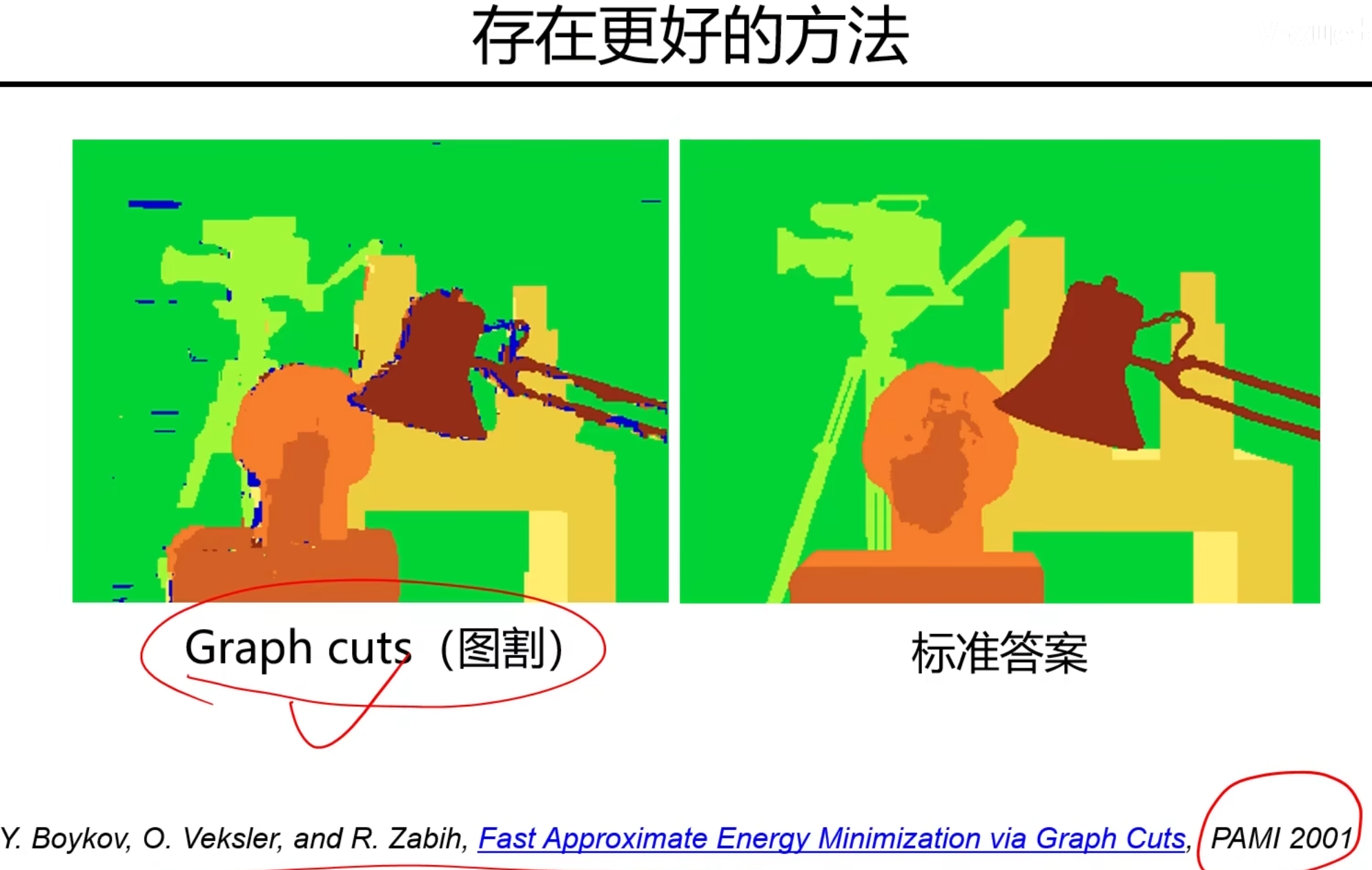
没有展开讨论
相关法的问题
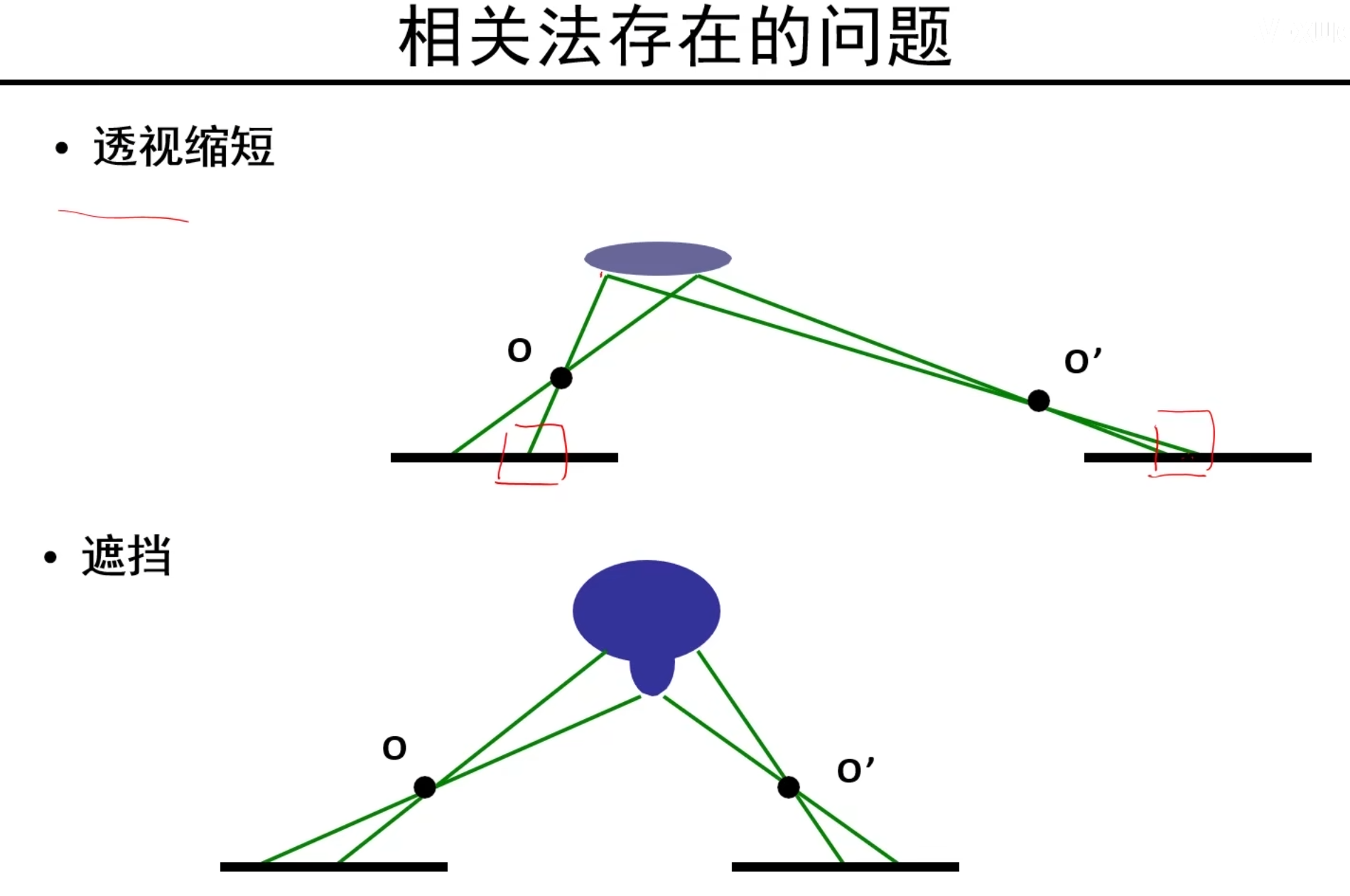
上图中同样大小窗口对应的实际范围完全不一样,左边对应一小块,右边对应一大片!
下图中可能发生遮挡问题,导致窗口映射的内容完全不一致
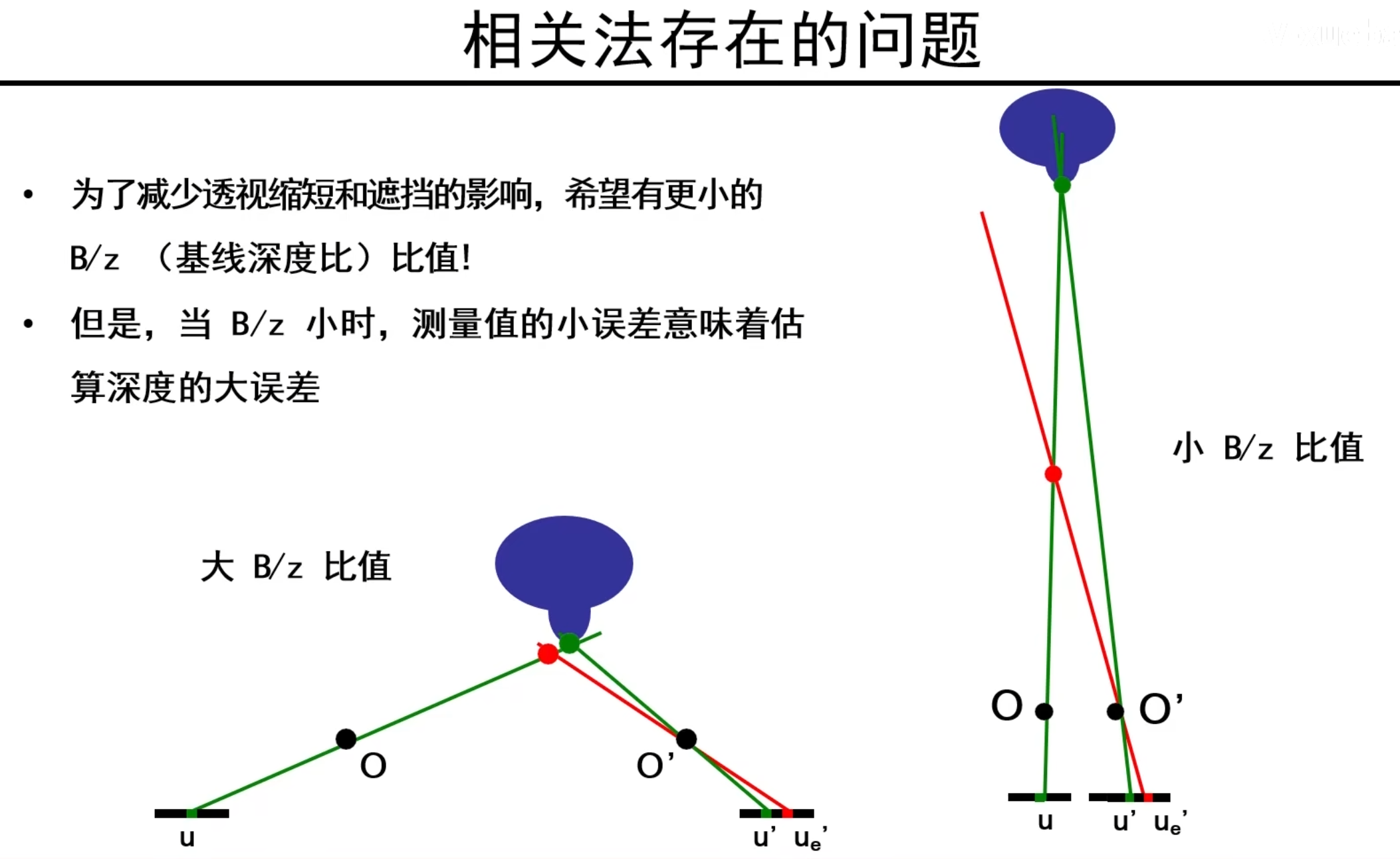
因为双目平行视觉系统的对应点关系只取决于B(基线距离),f(焦距),z(物体深度),因此我们只考虑改变这几个参数以权衡相关法存在的问题
为了减小透视缩短和遮挡问题,我们希望让物体的深度远一些,因此我们就需要更小的B,但是B小时,会导致深度z的估计误差变大!这也是一种trade-off

说明:瓷砖这一片都是同样的纹理,所以同质区域很难匹配

说明:左图一个点和右图很多点都可以对应,重复模式太多,不好匹配
总结:
遮挡,透视缩短,基线选择(由前两个决定),同质区域,重复性模式
添加约束以增加对应点匹配精确性
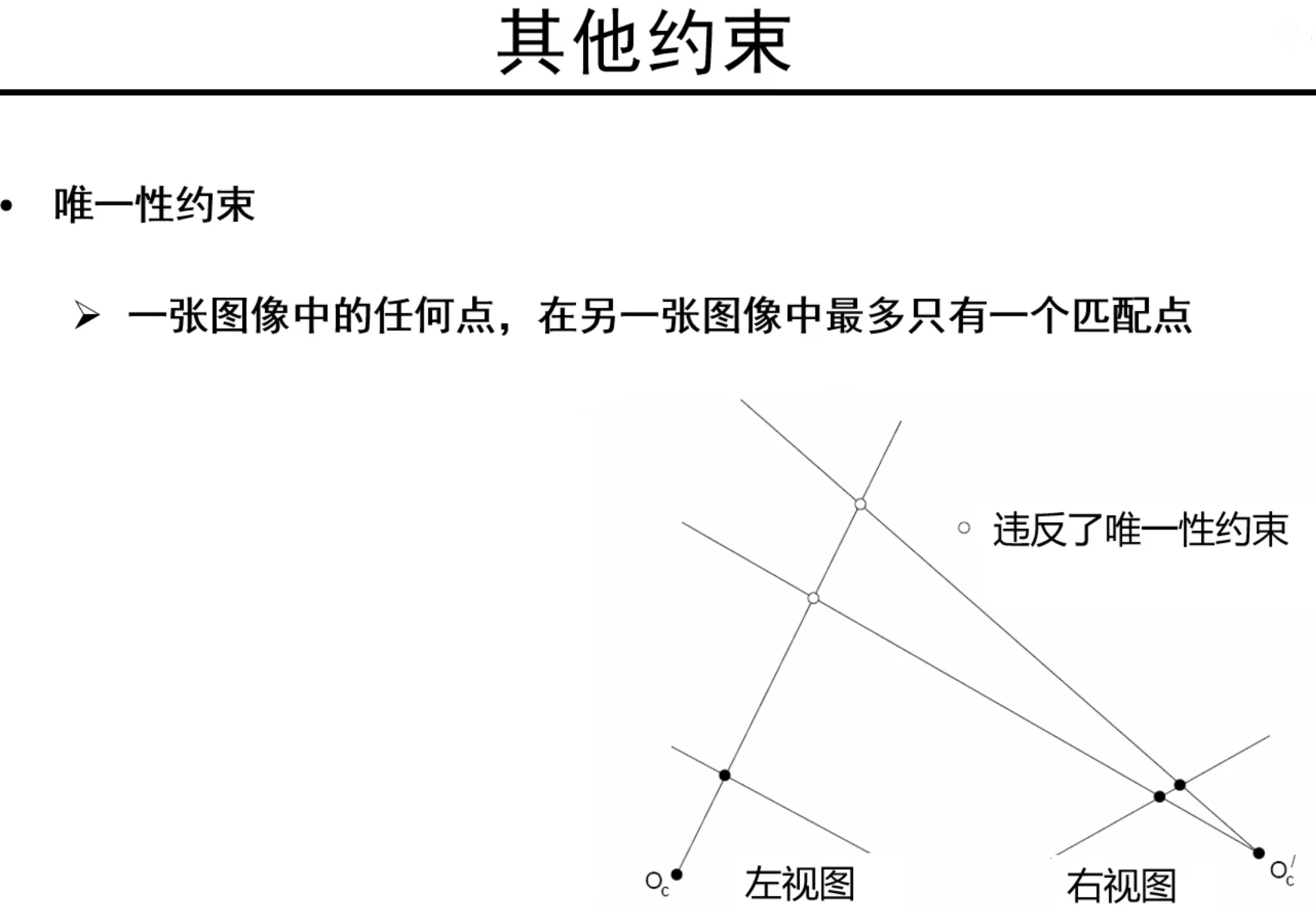
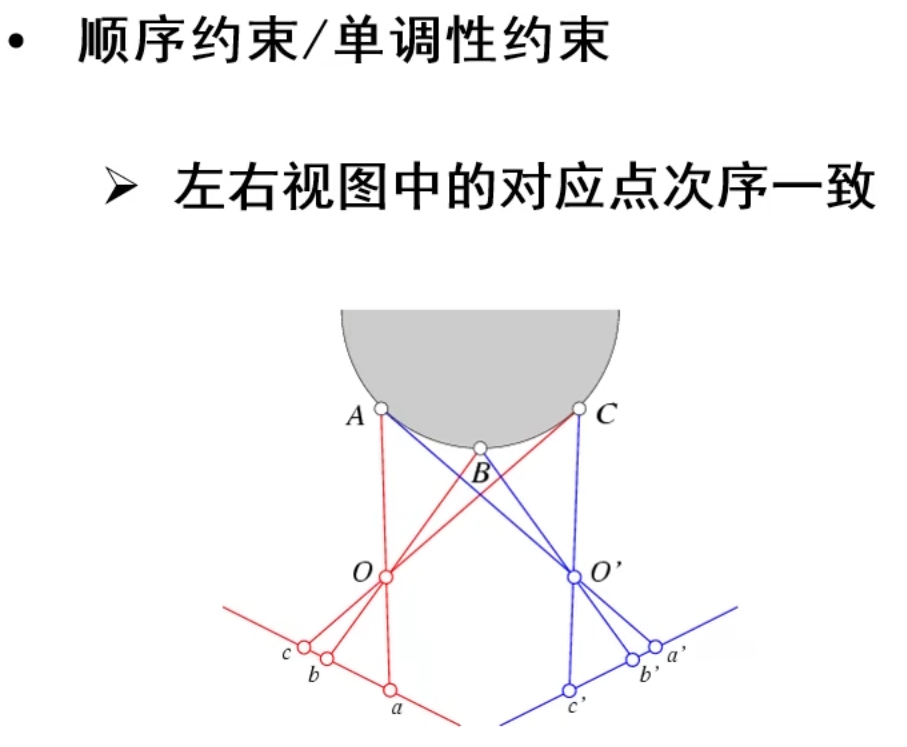

说明:平滑性意思是左图对应深度若是2,则右图对应深度不应该和2相差太大
6.多视图几何(运动恢复结构)
运动恢复结构问题(SfM)
通过三维场景的多张图像,恢复出该场景的三维结构信息以及每张图片对应的摄像机参数
SfM:Structure from Motion
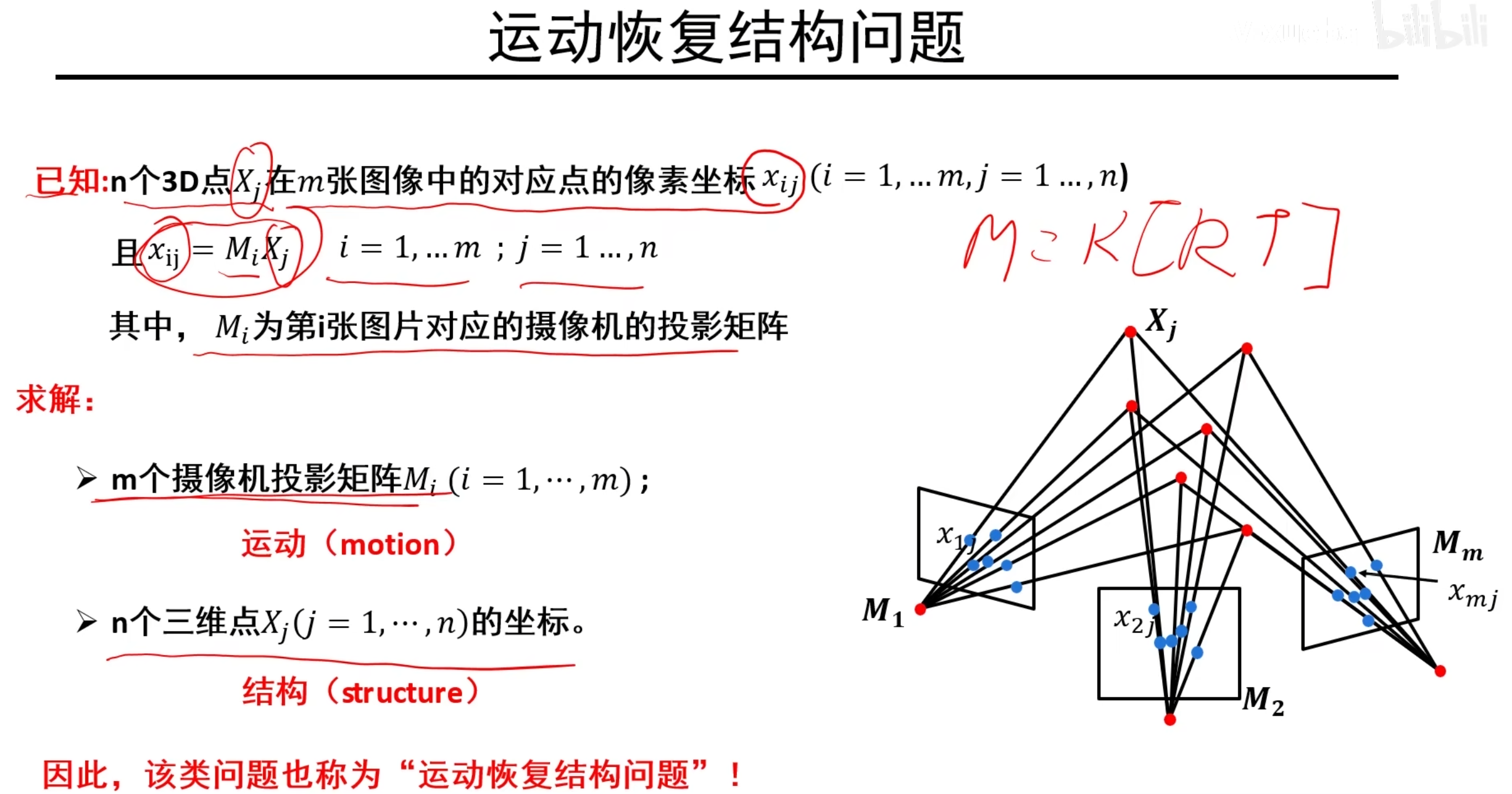
三种典型的运动恢复结构任务
欧式结构恢复(摄像机内参数已知,外参数未知)
欧式结构恢复问题:

欧式结构恢复的难点:
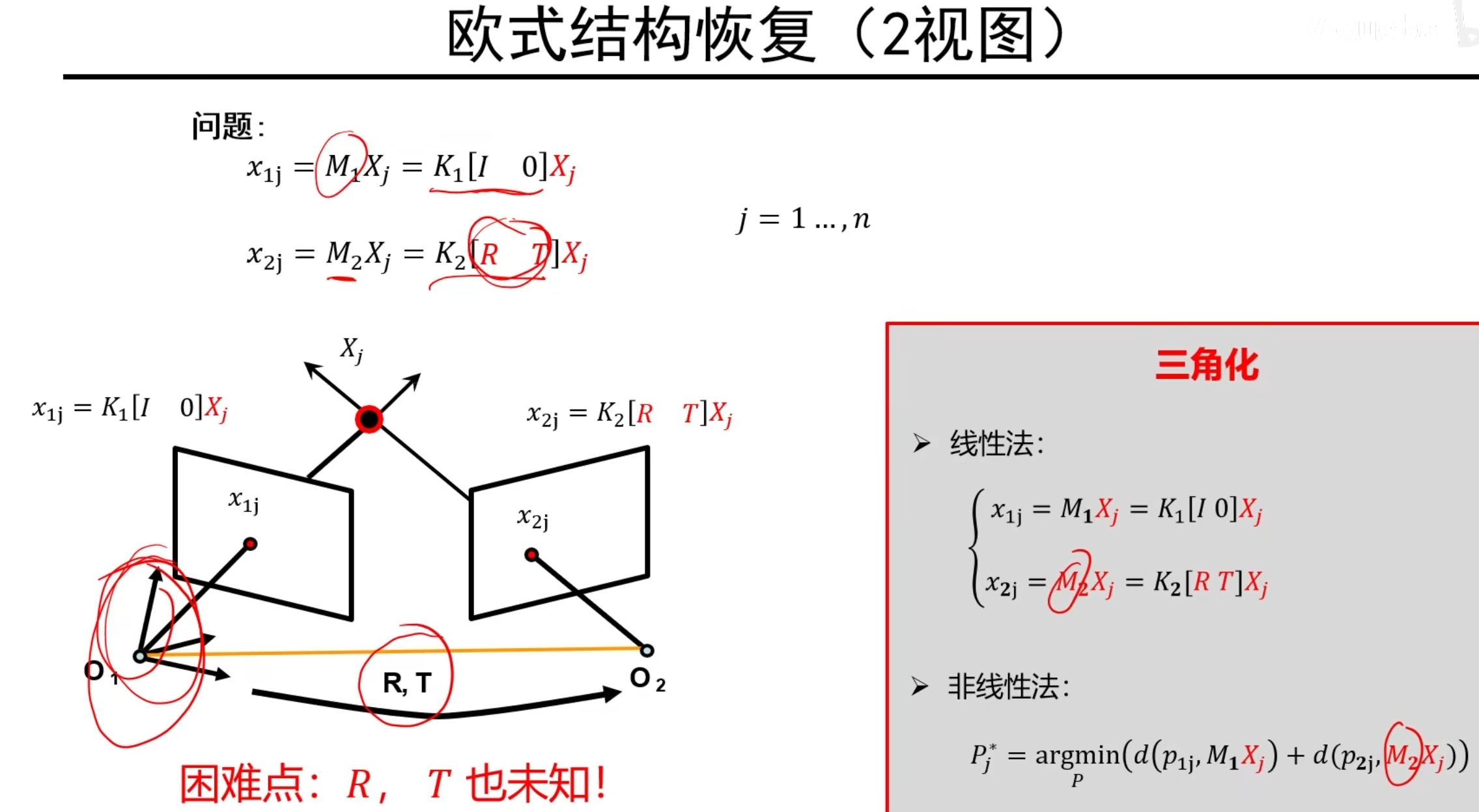
说明:回顾之前三角化,我们如果知道K,K’,R,T就可以恢复X~j~坐标,但是欧式结构中,我们如果假定O~1~相机为原点,那么O~2~相机的R,T外参数仍然未知,无法进行三角化。
思路:
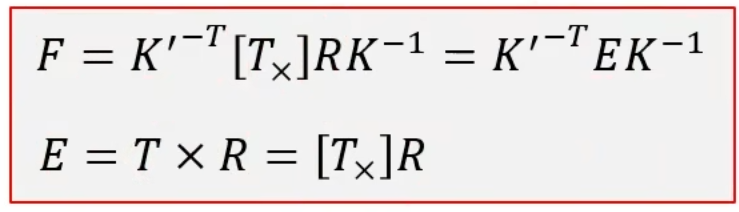
如果我们求得了基础矩阵F,因为欧式结构已知内参数,我们可以提取出本质矩阵E。得到E矩阵后,我们分解出T,R外参数矩阵,如此一来我们就可以使用原来的三角化恢复三维点坐标了。接下来我们看看具体的求解步骤:

我们可以发现,该问题求解中,只有第三步将本质矩阵E分解为R,T矩阵我们没有研究过,其他都学习过了,现在我们来详细研究该问题
本质矩阵E分解
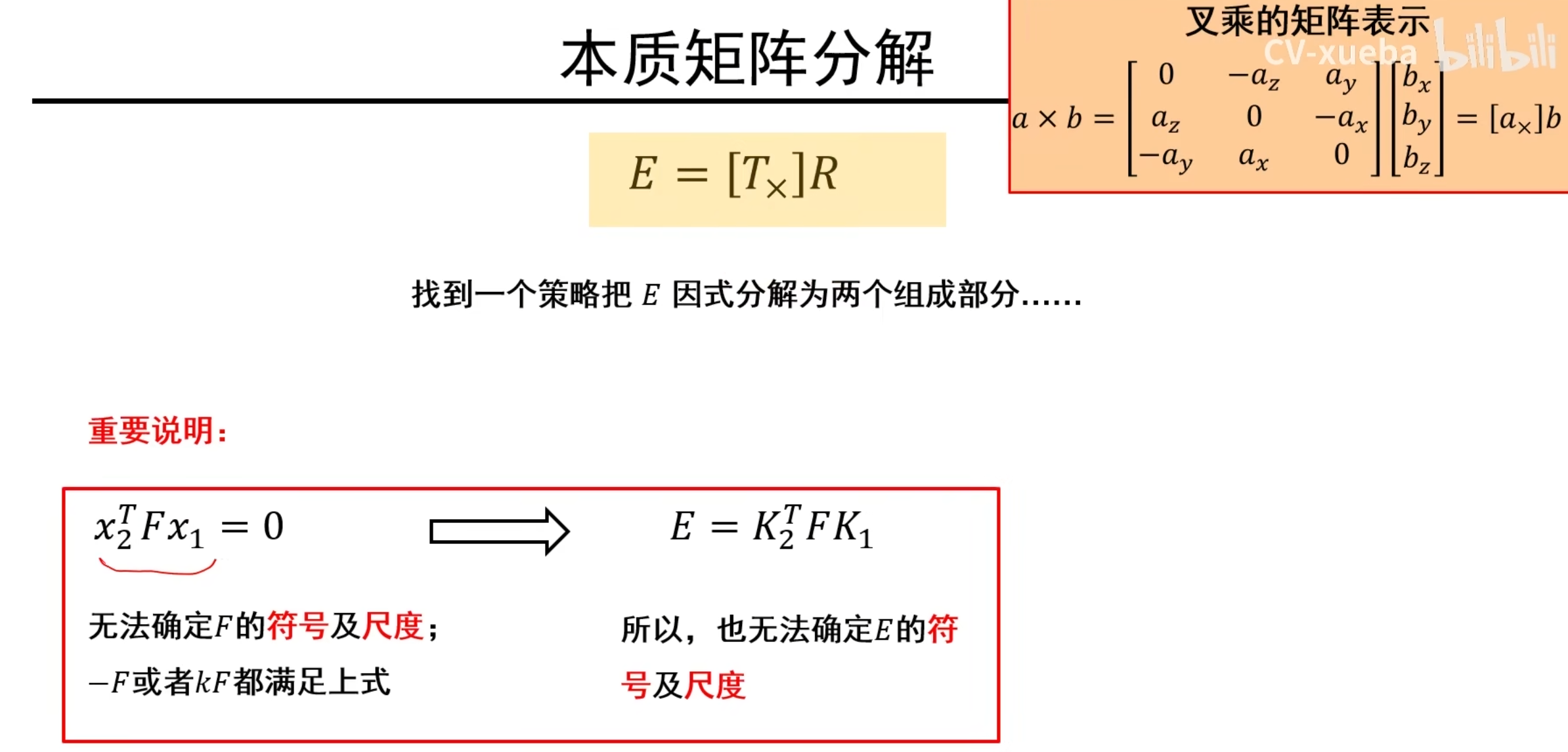
重要说明:我们求解F矩阵时,无法确定F的尺度,因为求得的F可能与实际解差系数,符号,因此我们不区分解的尺度,以后都不考虑尺度问题,因为我们无法确定真实尺度,我们只需要一个差一个系数的解就行。
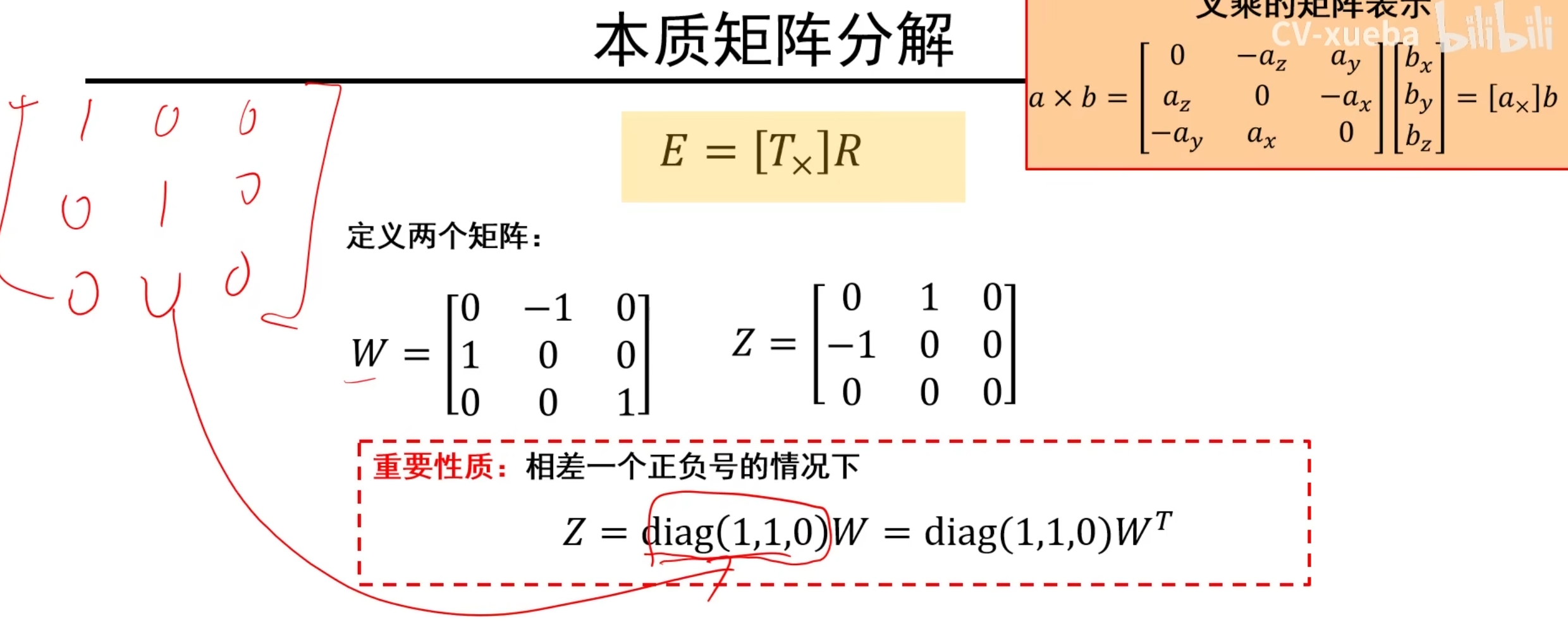
说明:上图是一个定义和性质,接下来需要使用

说明:上图也是一个结论,使用即可,其中Z是上上图里面的Z矩阵

说明:进一步地,我们不关注尺度符号,因此T矩阵可以进一步简化成右边式子
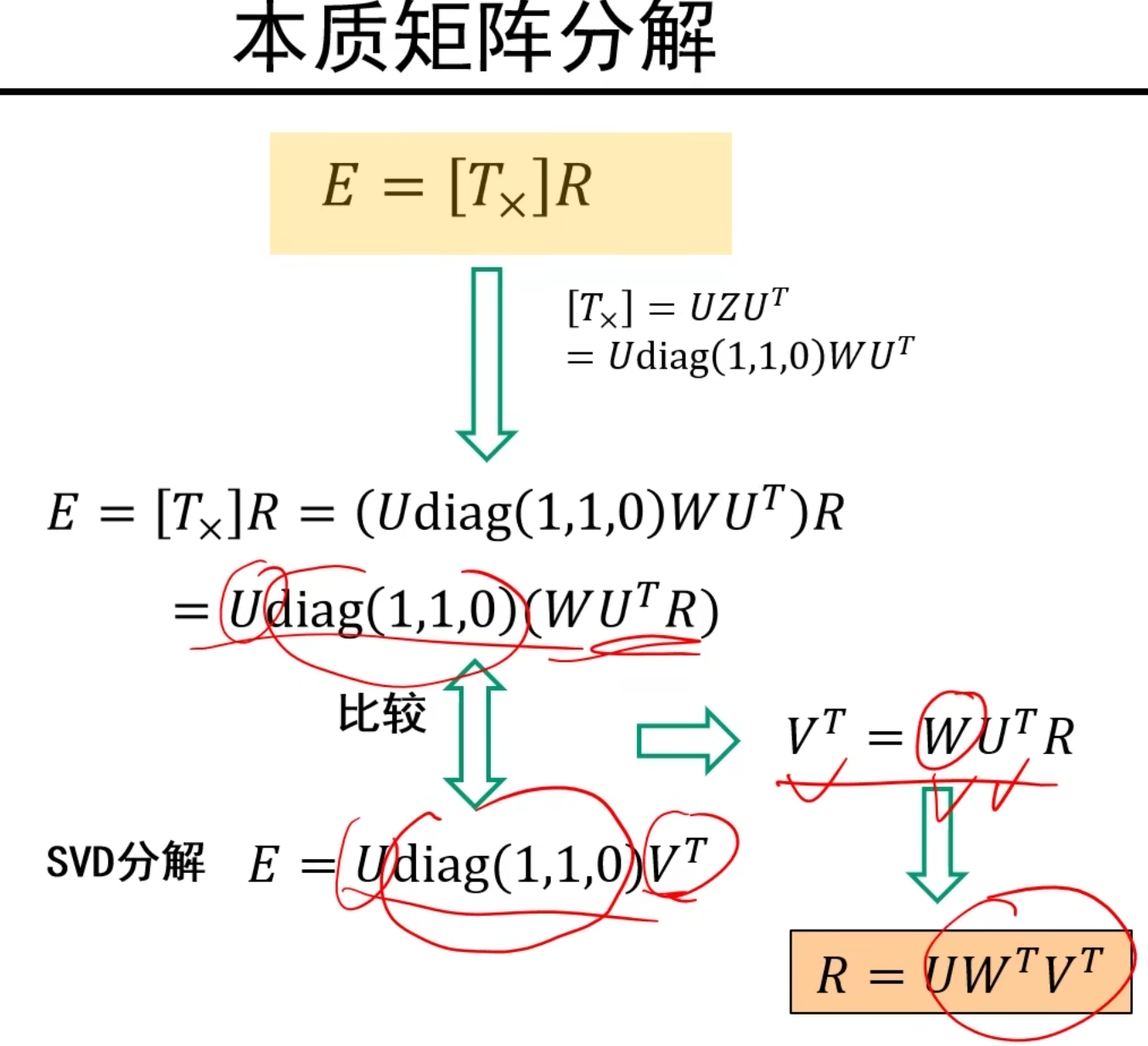
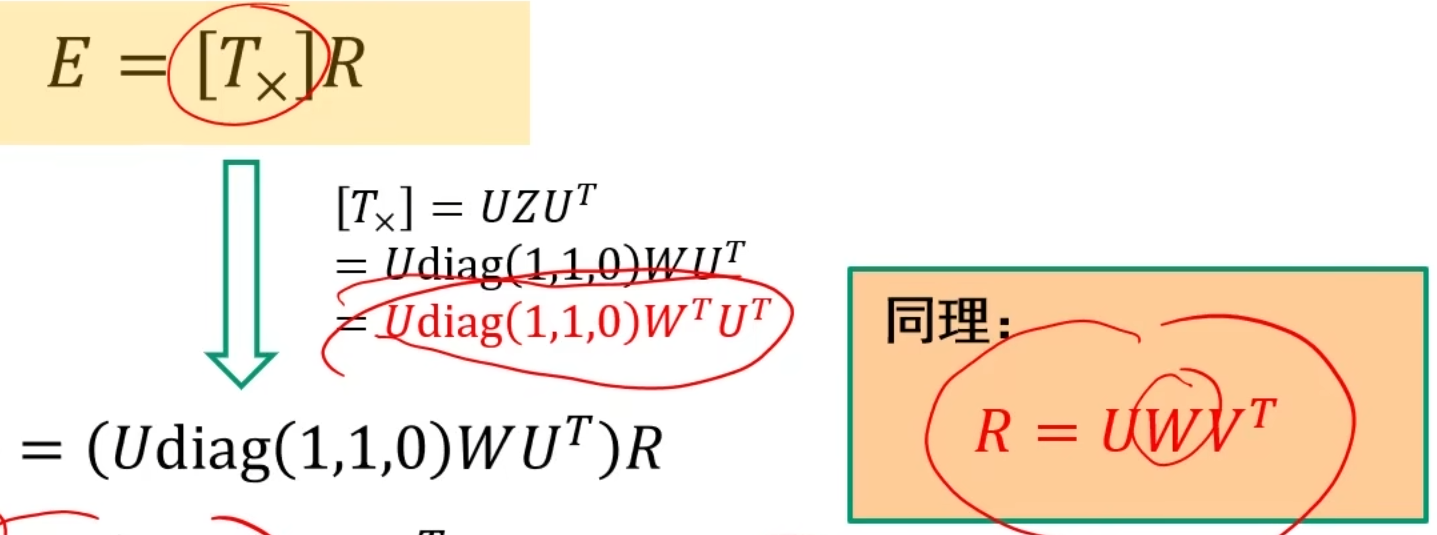
说明:将上面的式子代入E矩阵,化简得到E的第一个分解式子,同时,我们直接调包对E矩阵进行奇异值分解(SVD)就可以得到下面的结果,上下两式进行比较,由于奇异值分解我们可以得到U,V^T^的表达式,所以整个式子中只有R未知,我们于是可以得到R矩阵的表达式
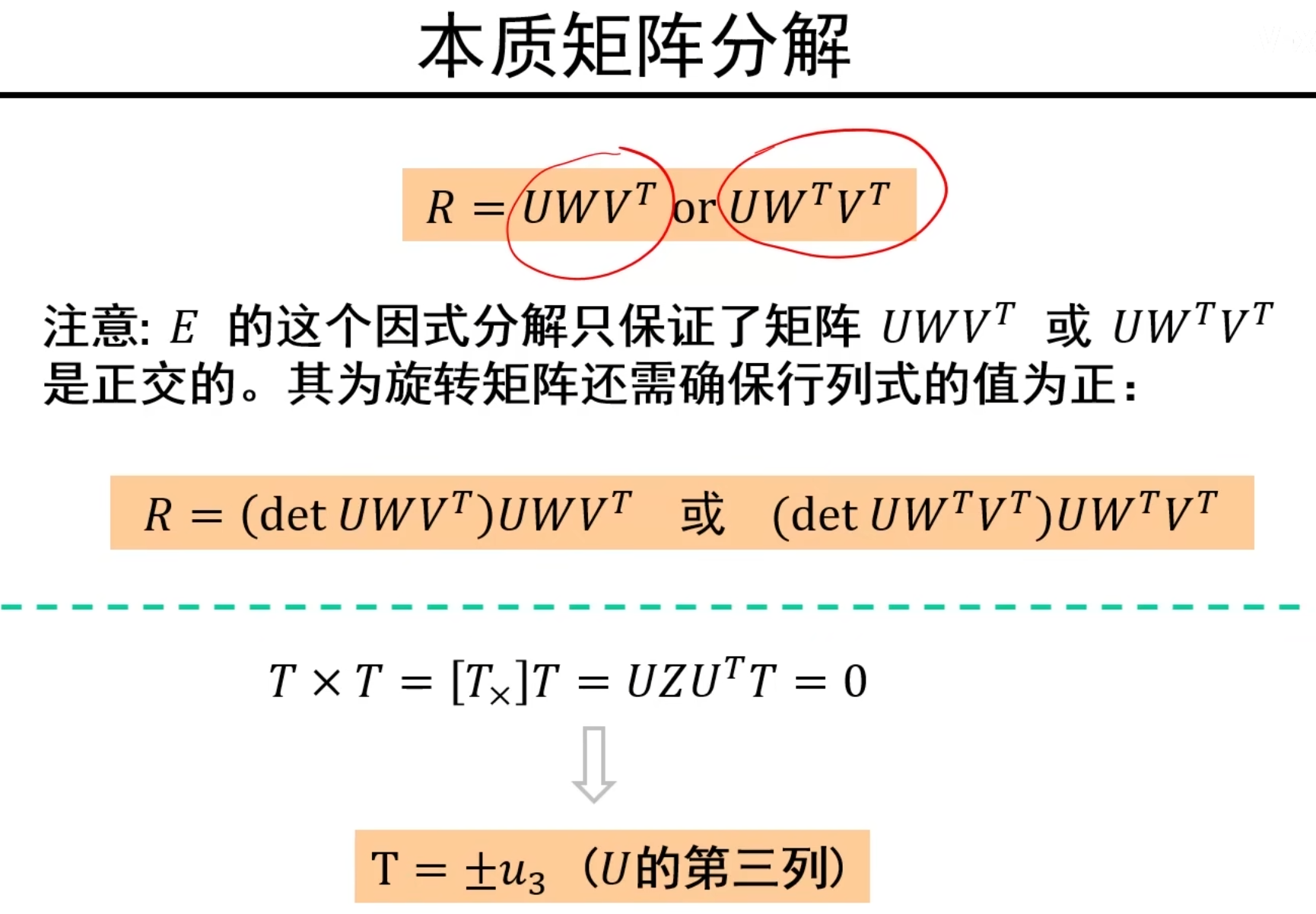
说明:代入一下旋转矩阵可以发现,旋转矩阵的行列式为1才行,如果是-1会导致是一个带有镜像翻转的旋转。
接下来,我们要求T矩阵,使用T X T=0,如上图,叉乘式子变成一个Ax=0的方程,其中A=[T~X~],x=T,这是一个齐次线性方程组,可以再次使用奇异值分解求解!奇异值分解以后就可以得到T矩阵的表达式了。
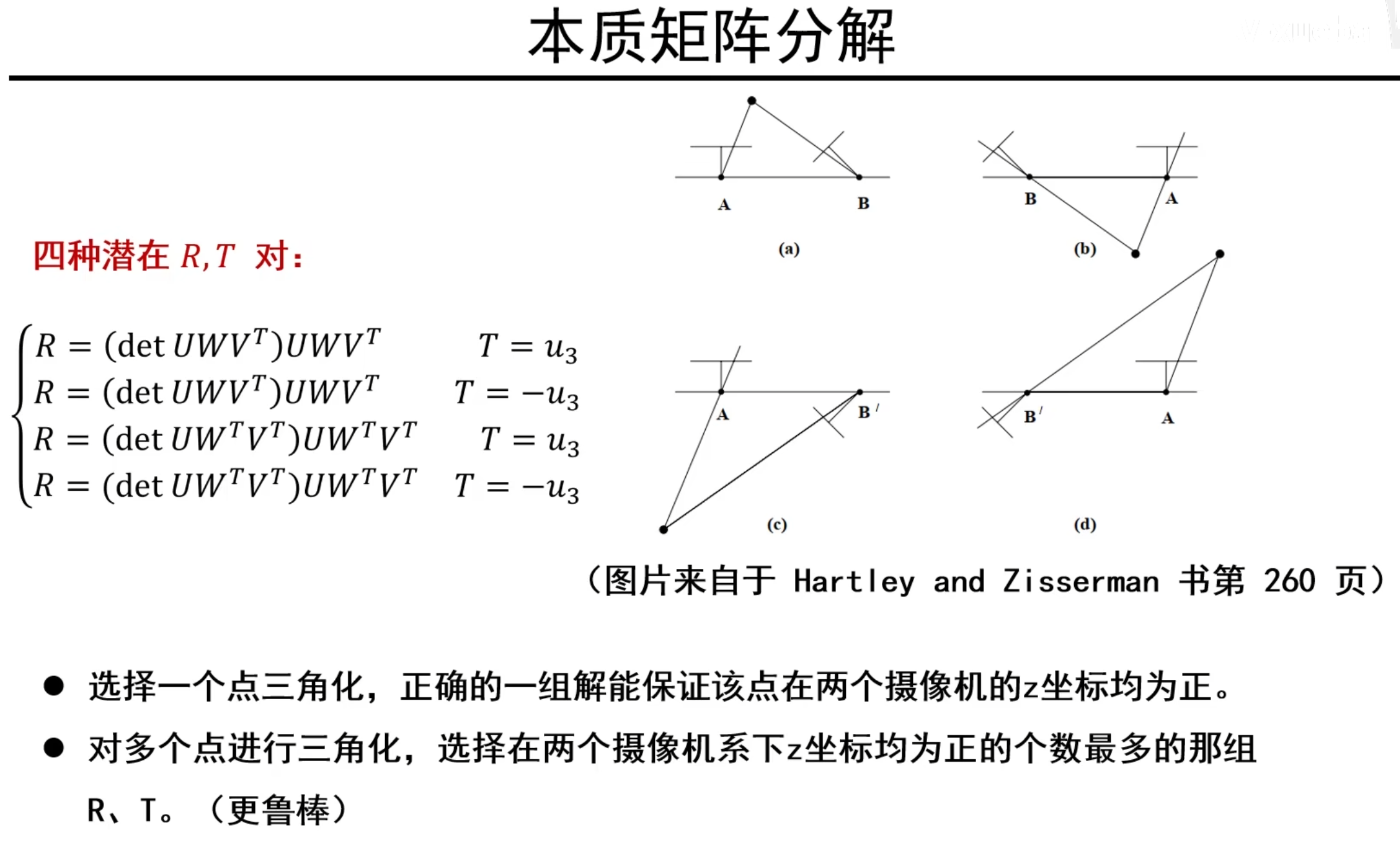
说明:符号问题,我们可以得到R,T的表达式组合有四种,如何取得正确的R,T组合呢?
我们在实际中,拿得到的R,T进行多个点的三角化,正确的解能确保点在两个摄像机的z坐标均为正。但是难免有噪声,因此我们就找在两个摄像机下z坐标均为正的个数最多的那组R,T。
本质矩阵分解的总结

欧式结构恢复的歧义
我们不能估计场景的绝对尺度(绝对大小等)
我们恢复的结构与真实场景之间还相差一个相似变换(旋转,平移,缩放),因为我们求解恢复的三维点的坐标是以O~1~相机为原点的摄像机坐标系下的。这是一种度量重构
度量重构:恢复的场景与真实场景之间仅存在相似变换的重构
仿射结构恢复(摄像机为仿射相机,内外参数均未知)
仿射相机投影矩阵化简
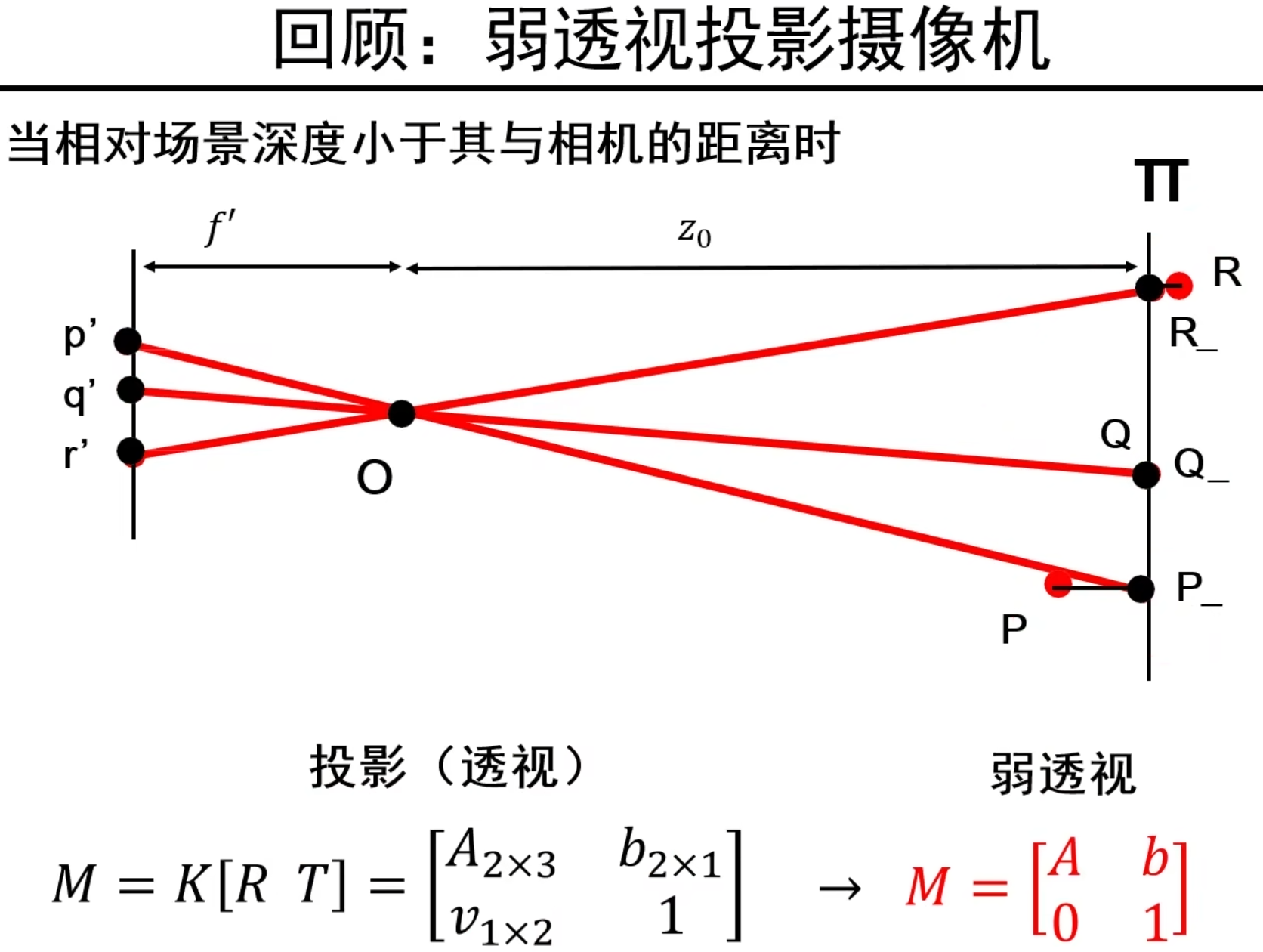
说明:弱透视投影摄像机的M矩阵其实是一个仿射变换(推导没有讲),因此M矩阵可以写成仿射变换的形式如上图红色部分。
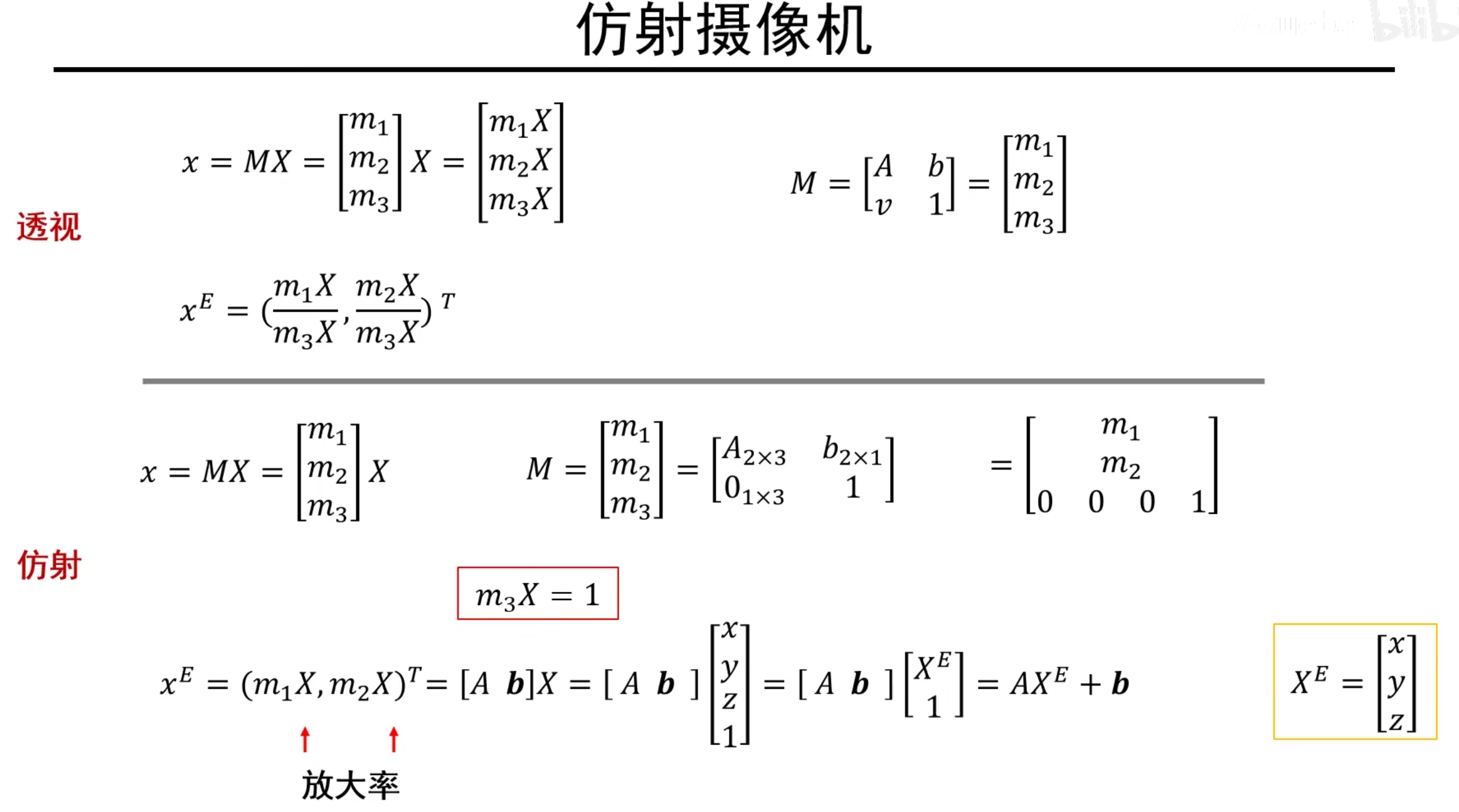
说明:x^E^代表x点在欧式空间的坐标
底下的仿射中,因为仿射变换第三行是0001,所以可以得到m~3~X=1
仿射相机结构恢复问题重述
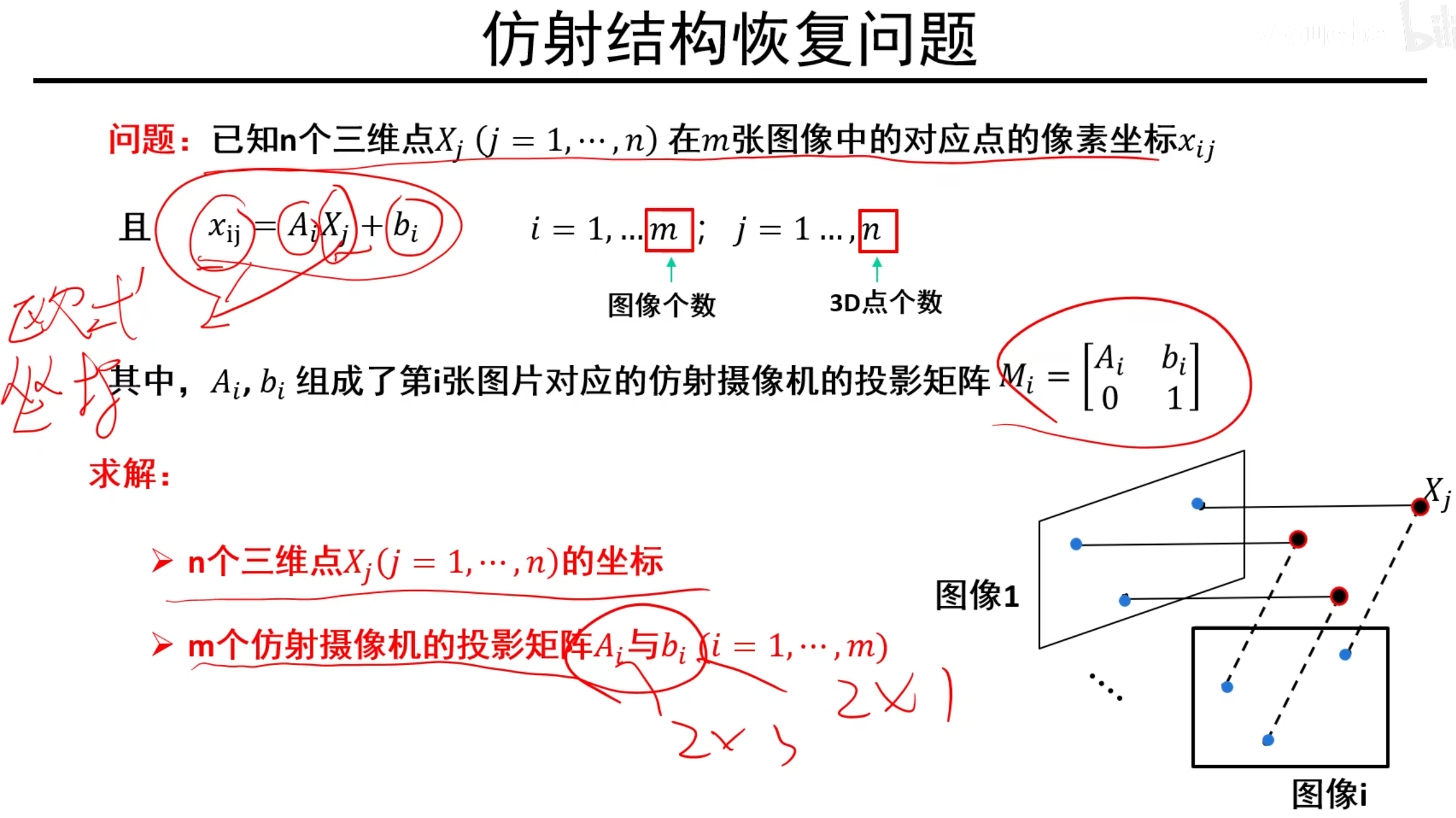
因式分解的仿射结构恢复

数据中心化
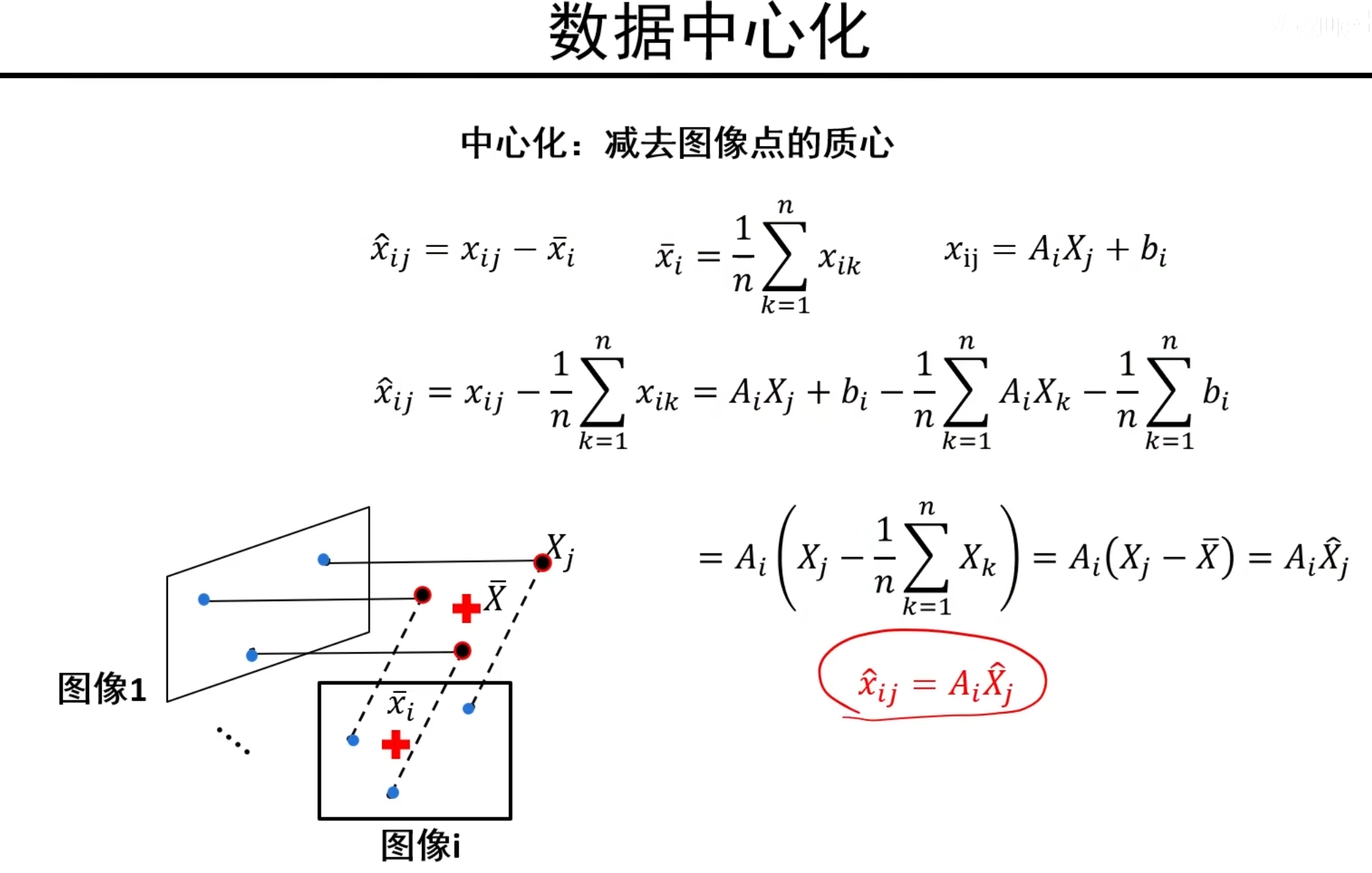
说明:我们得到了三维点去均值后与二维点去均值后的新关系,不再有b这个位移系数
进一步思考,如果我们把三维坐标的原点从O~1~坐标移动到三维这些X点的质心处,好处就是这里的去均值后三维坐标就是不去均值的三维坐标,因为质心坐标就是(0,0,0)原点!
所以我们可以进一步推出 =A~i~X~j~
把刚刚的新关系写成矩阵形式,如下:
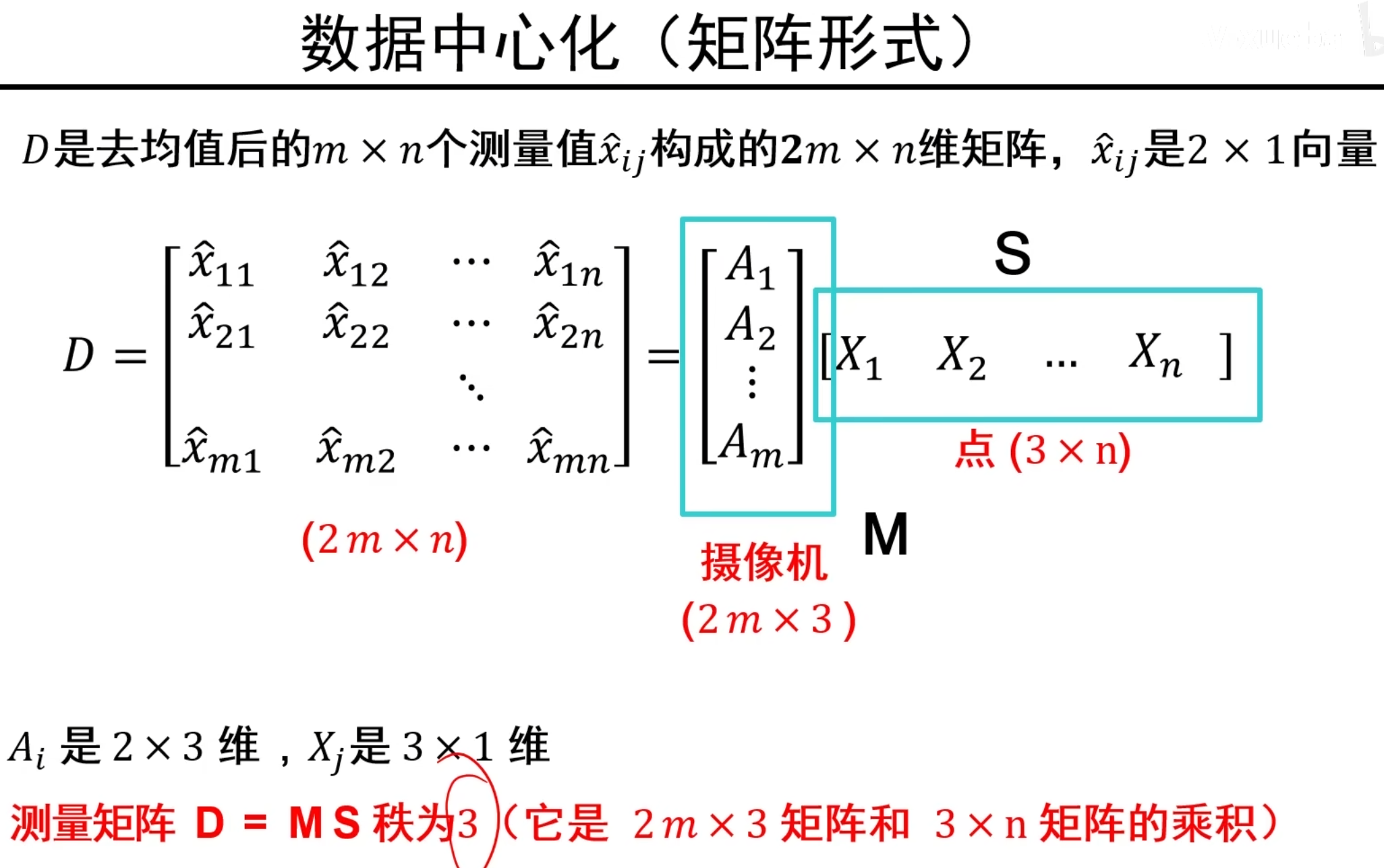
说明:M,S矩阵未知,D矩阵已知。要像求解M,S矩阵,我们又要对D矩阵进行某种分解。
因式分解
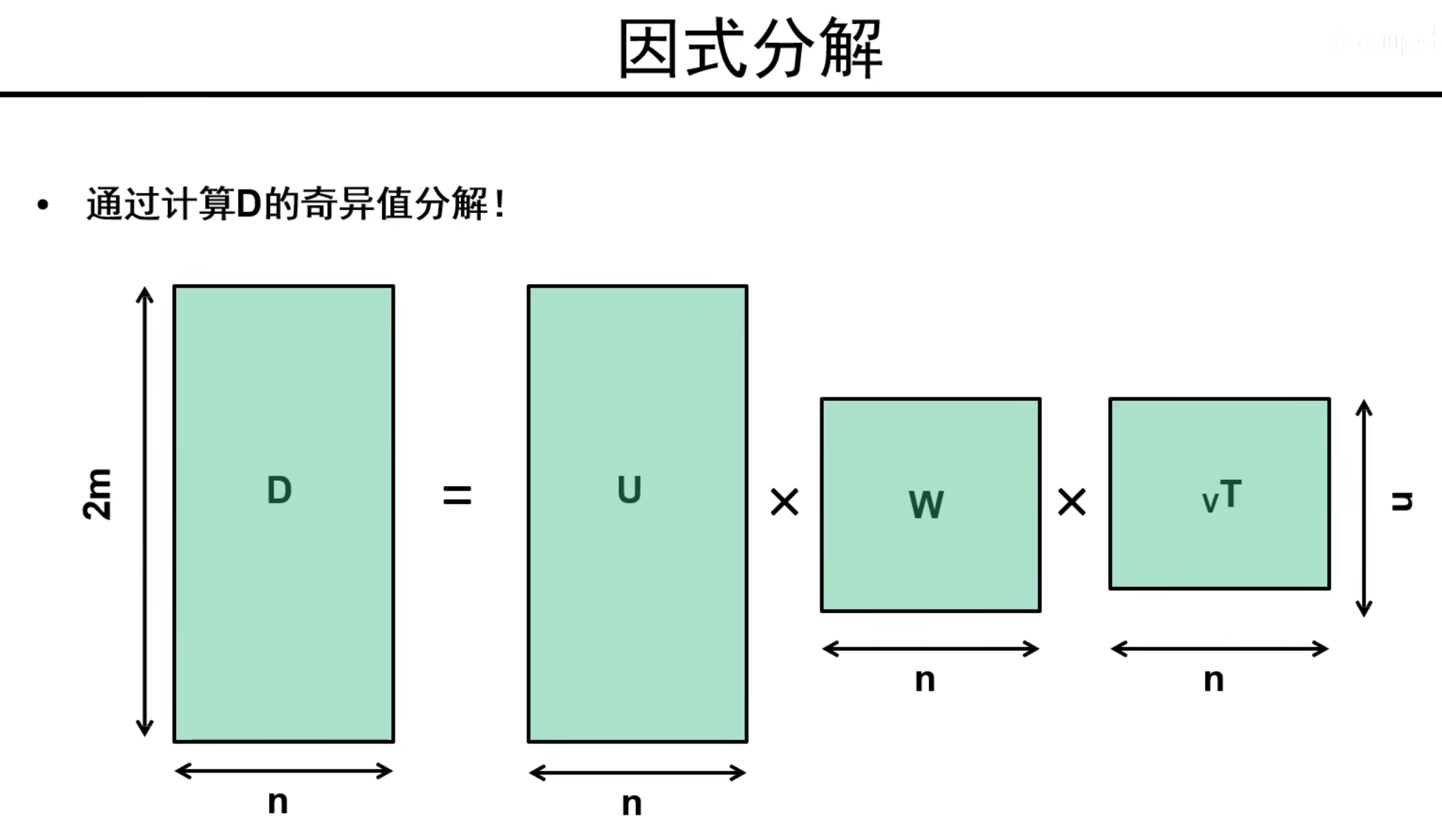
说明:对D进行奇异值分解!得到上图三个矩阵
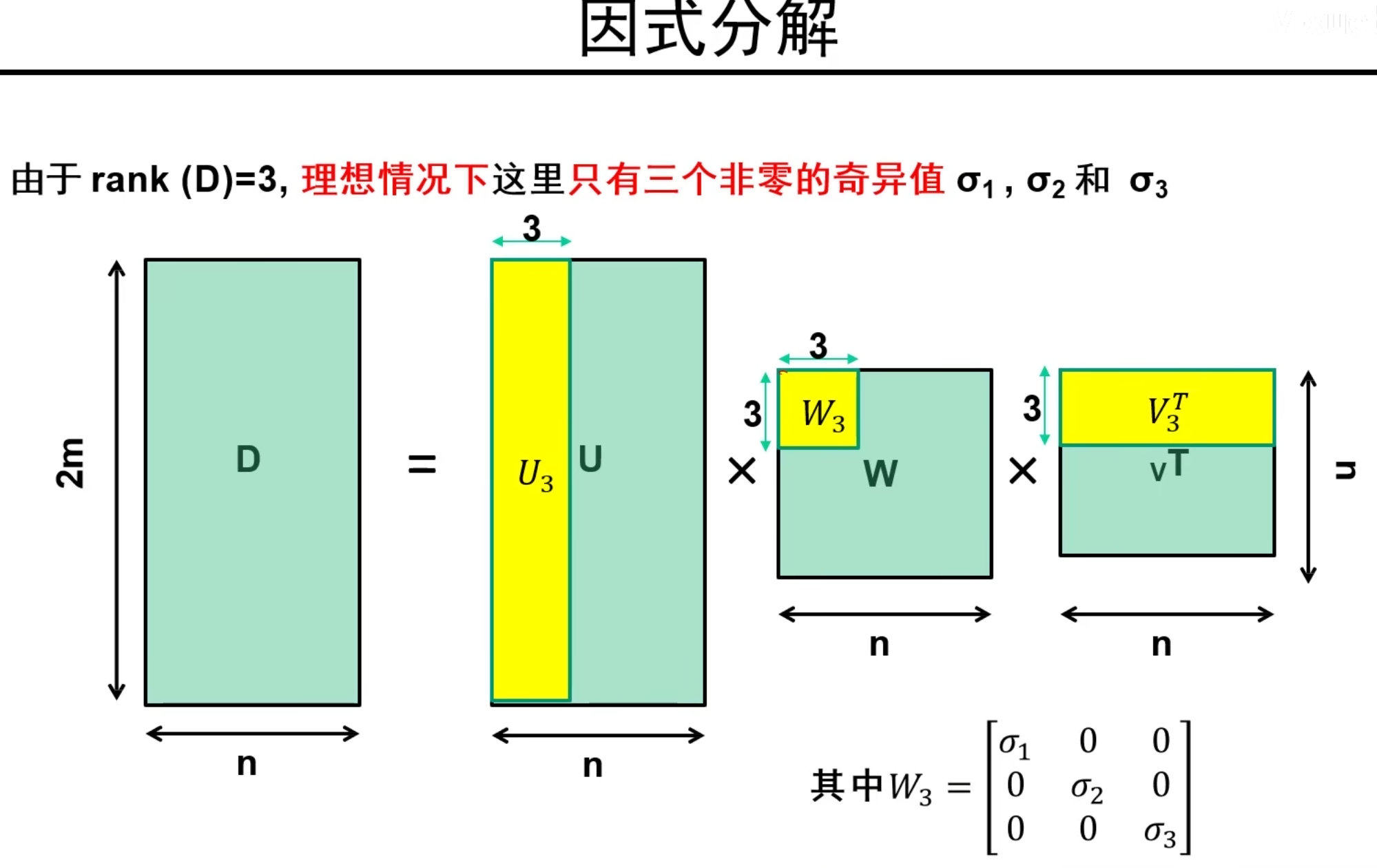
说明:因为D矩阵的秩是3,因此只取最大的三个特征值对应的部分如上图
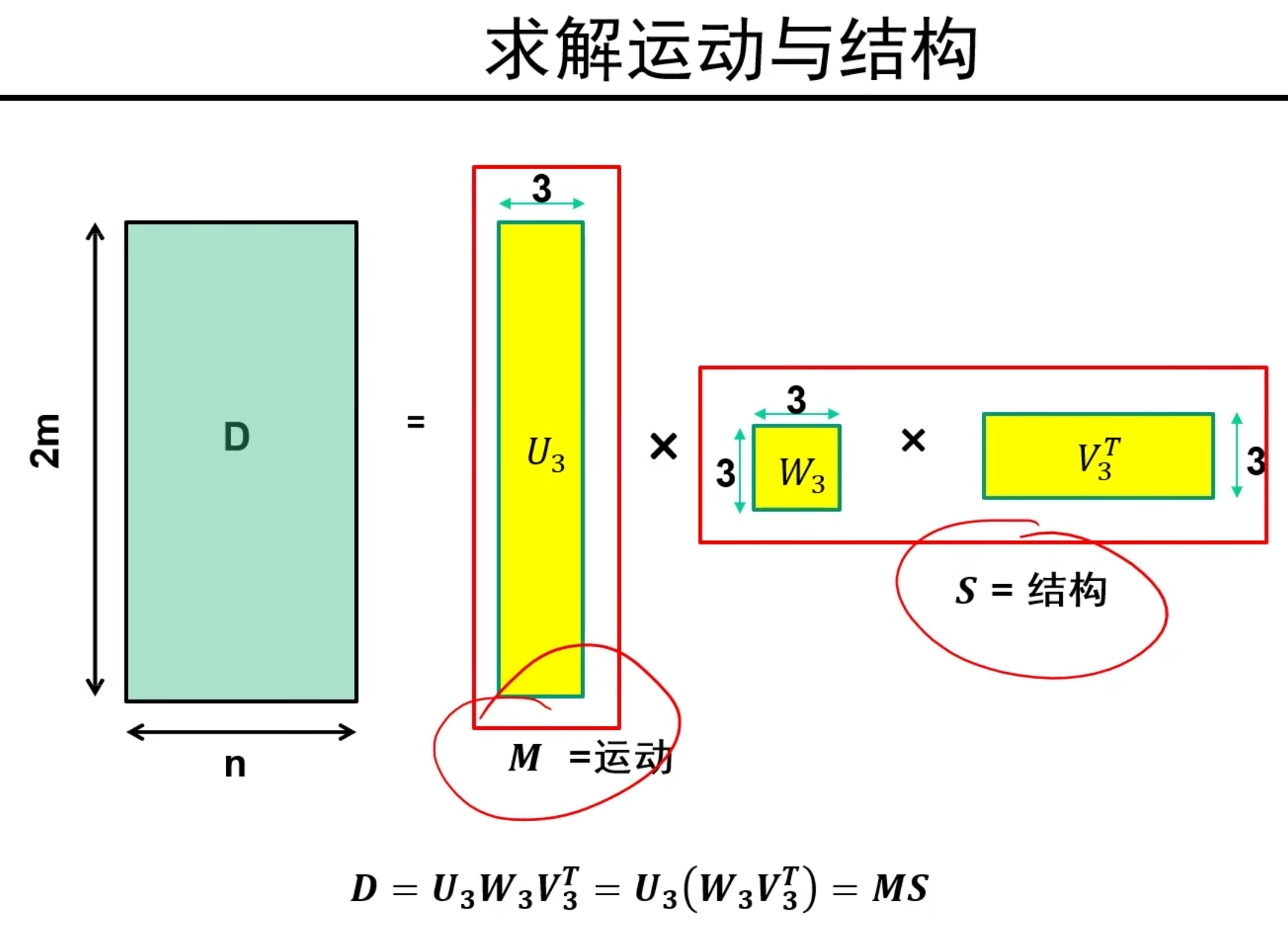
说明:得到上图,我们就可以让2m*3部分的矩阵为M矩阵,剩下的为S矩阵!
当然,也可以按下图进行分解:
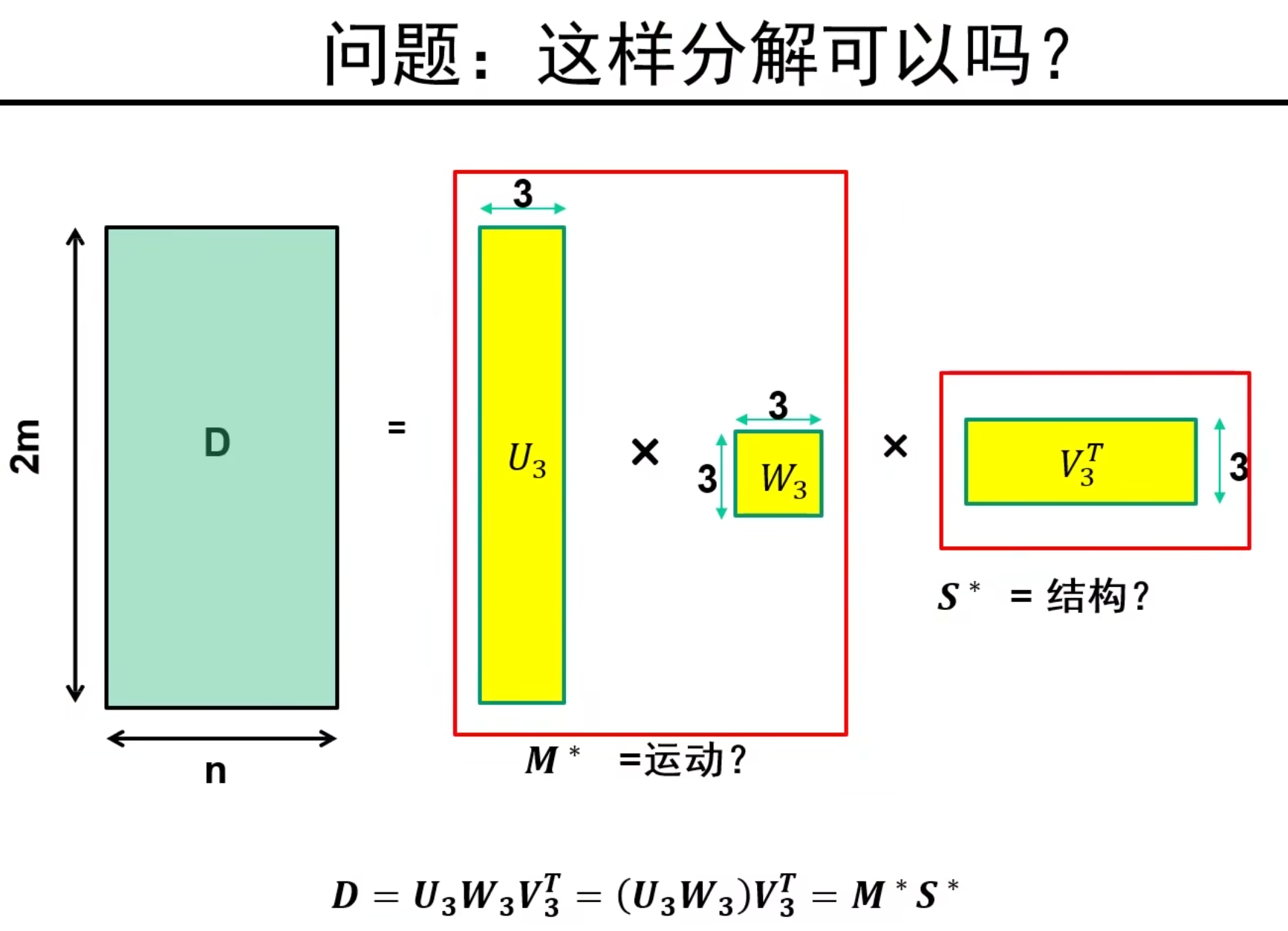
仿射结构恢复总结

仿射结构恢复歧义
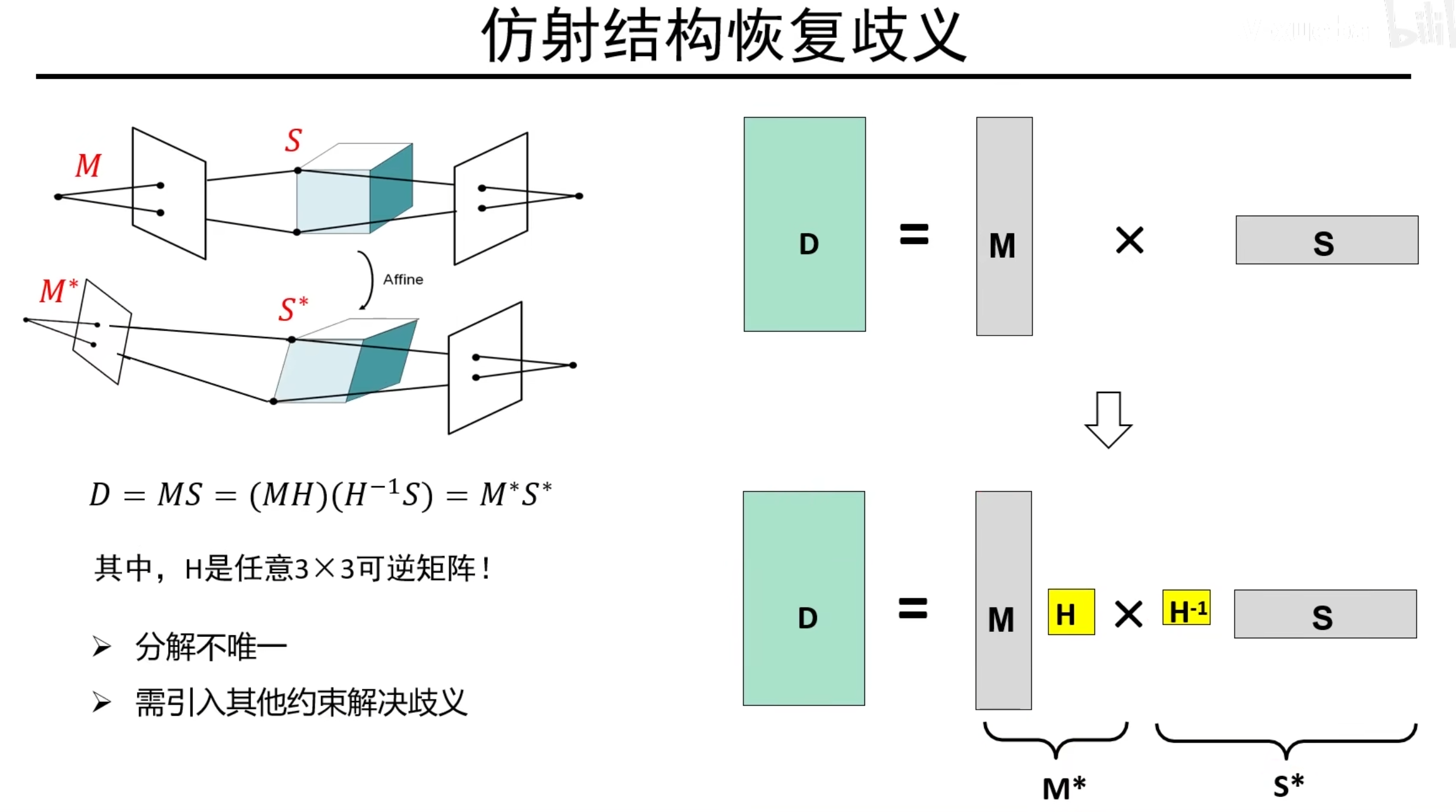
说明:我们求解的M,S矩阵其实和真实的差了一个可逆的3x3 H矩阵,这个3x3矩阵会造成旋转,措切,缩放等效果。

说明:m个相机,n个三维点,可以列出2mn个等式
一个相机的仿射变换矩阵的A有6个未知,b有2个未知,所以m个有8m个未知
每个三维点有3个未知,n个三维点有3n个未知
最后求解完以后因为差了一个H矩阵差异,这里有8个未知量(本身是9个未知量,但是可以通过齐次除法去掉一维,也就是8个)
所以要想恢复仿射结构,必须满足 2mn >= 8m + 3n - 8
透视结构恢复(摄像机为透视相机,内外参数均未知)
透视结构恢复歧问题重述
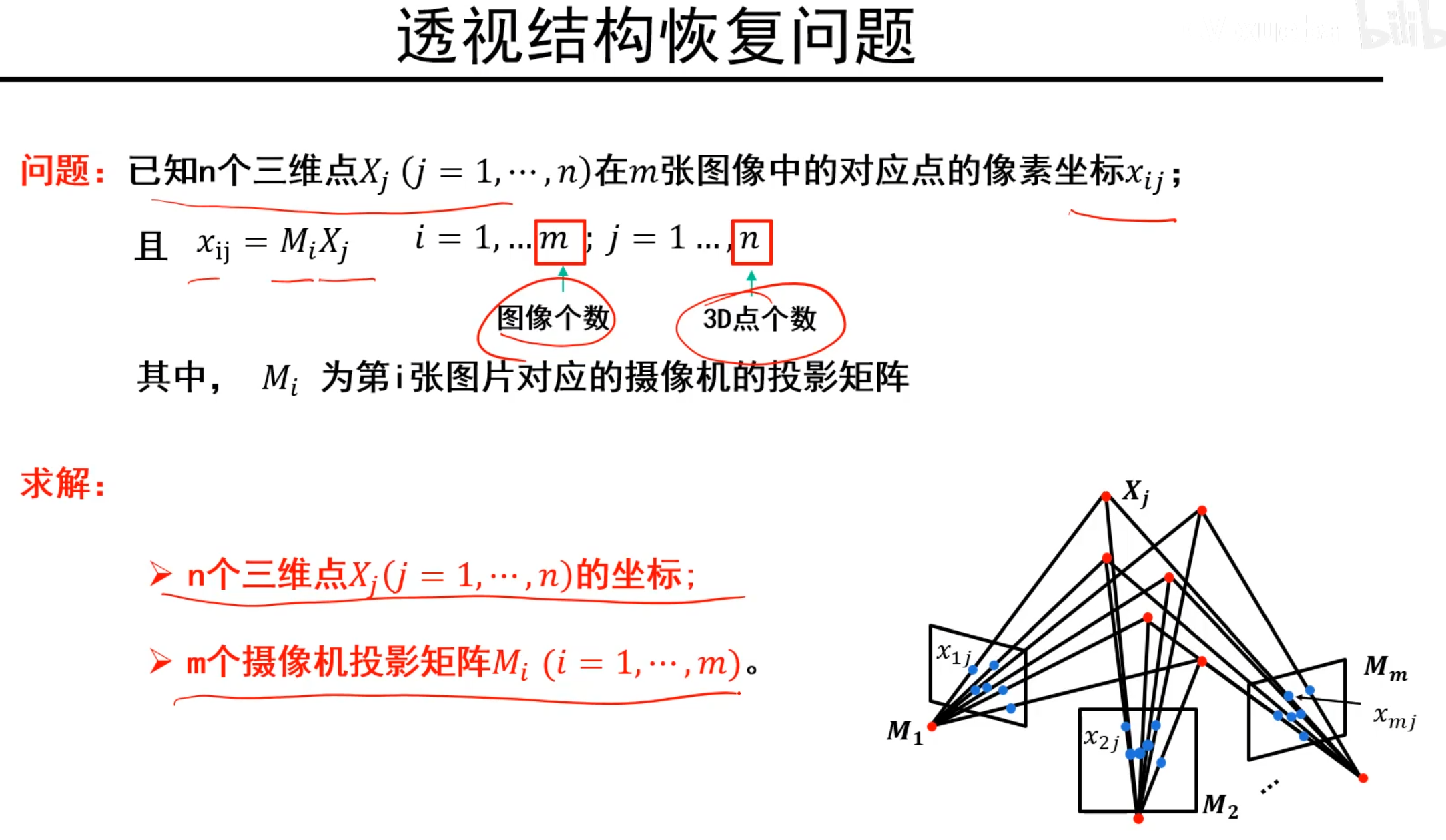
透视结构恢复的歧义
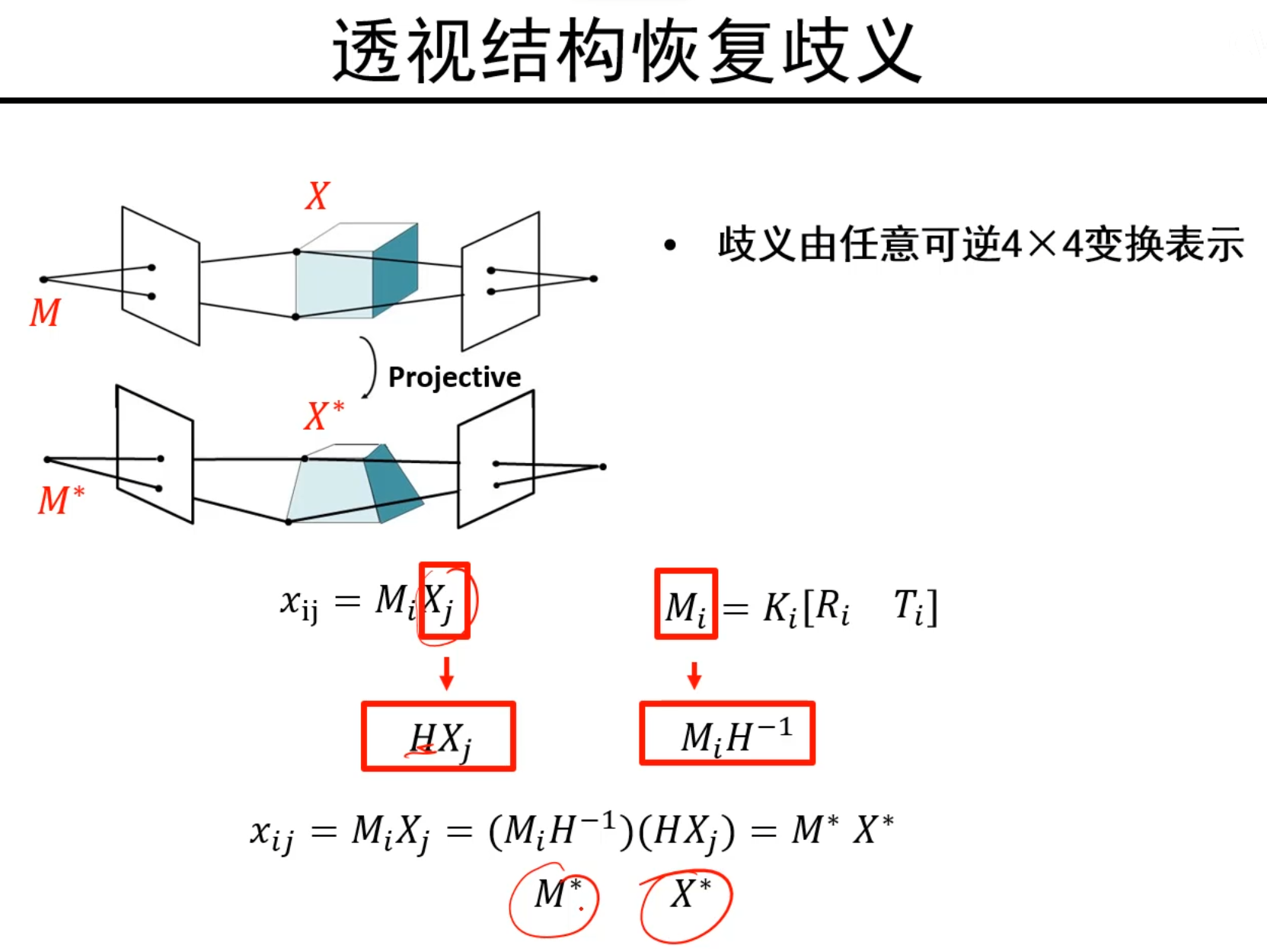
乘上一个4x4可逆矩阵H,得到仍然是符合条件的解,所以透视结构恢复也是存在歧义的,仿射结构恢复中的歧义是3x3的可逆矩阵。
代数方法(基础矩阵)
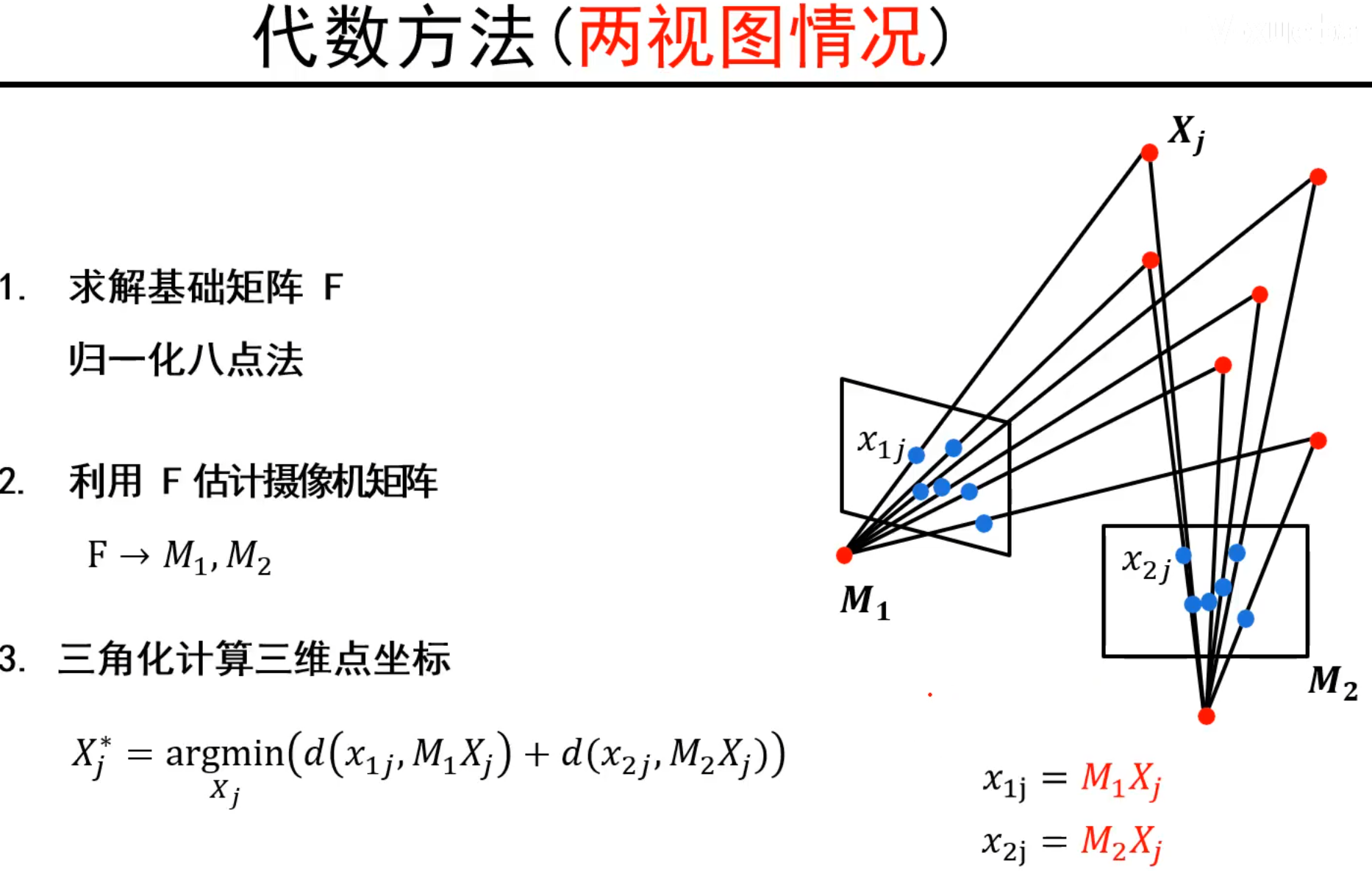
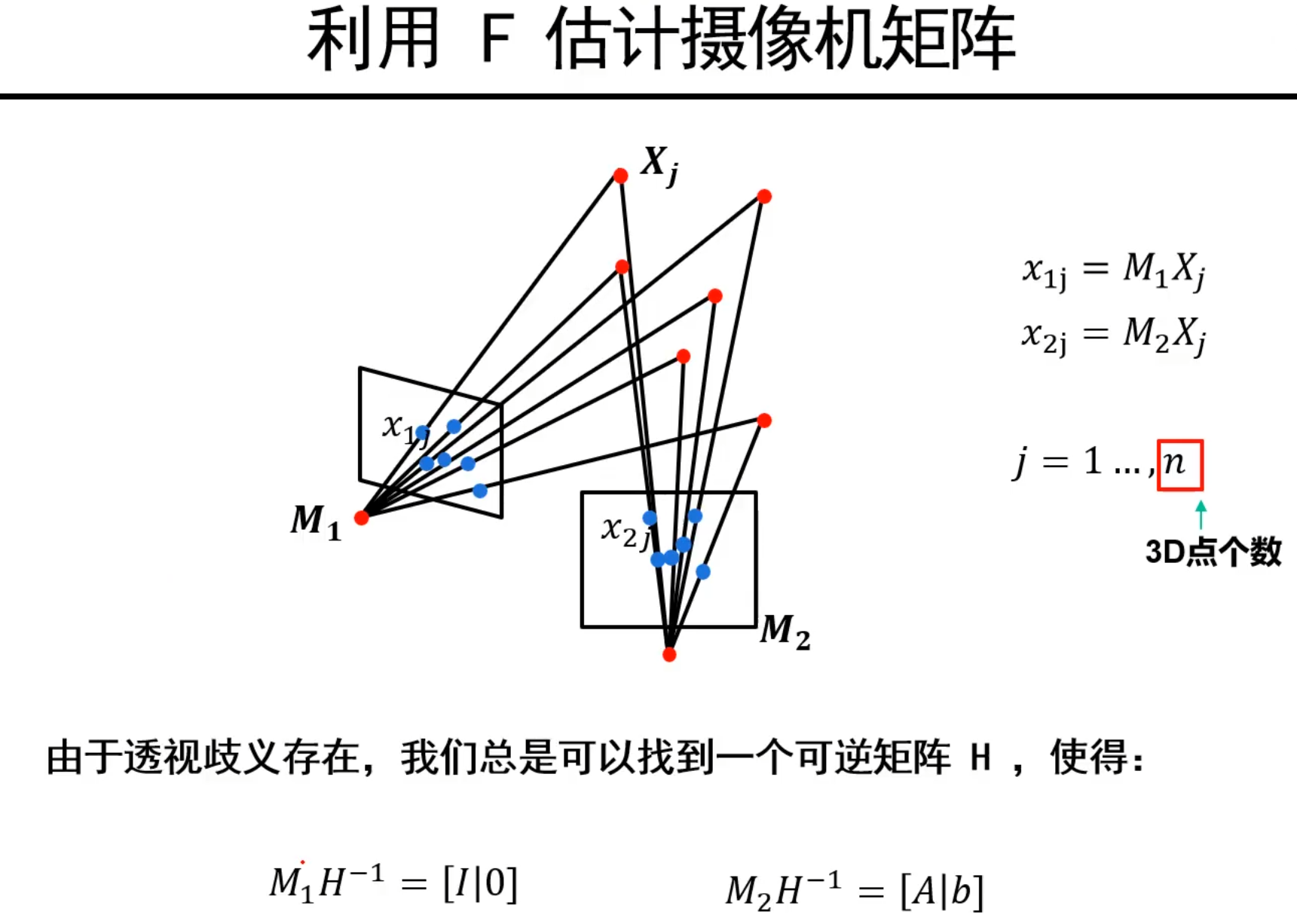
说明:由于透视歧义存在,我们就让M~1~矩阵经过一个H变成单位阵形式记作M~1~^^或者,这样对应得M~2~也会变换记作M~2~^^,这样相当于我们已经知道了M~1~^^的值,只需要计算得到M~2~^^,就可以通过三角化得到变换后的三维点X~j~^*^。
推导F矩阵的新表达

计算A和b

b是什么?
回顾极几何:
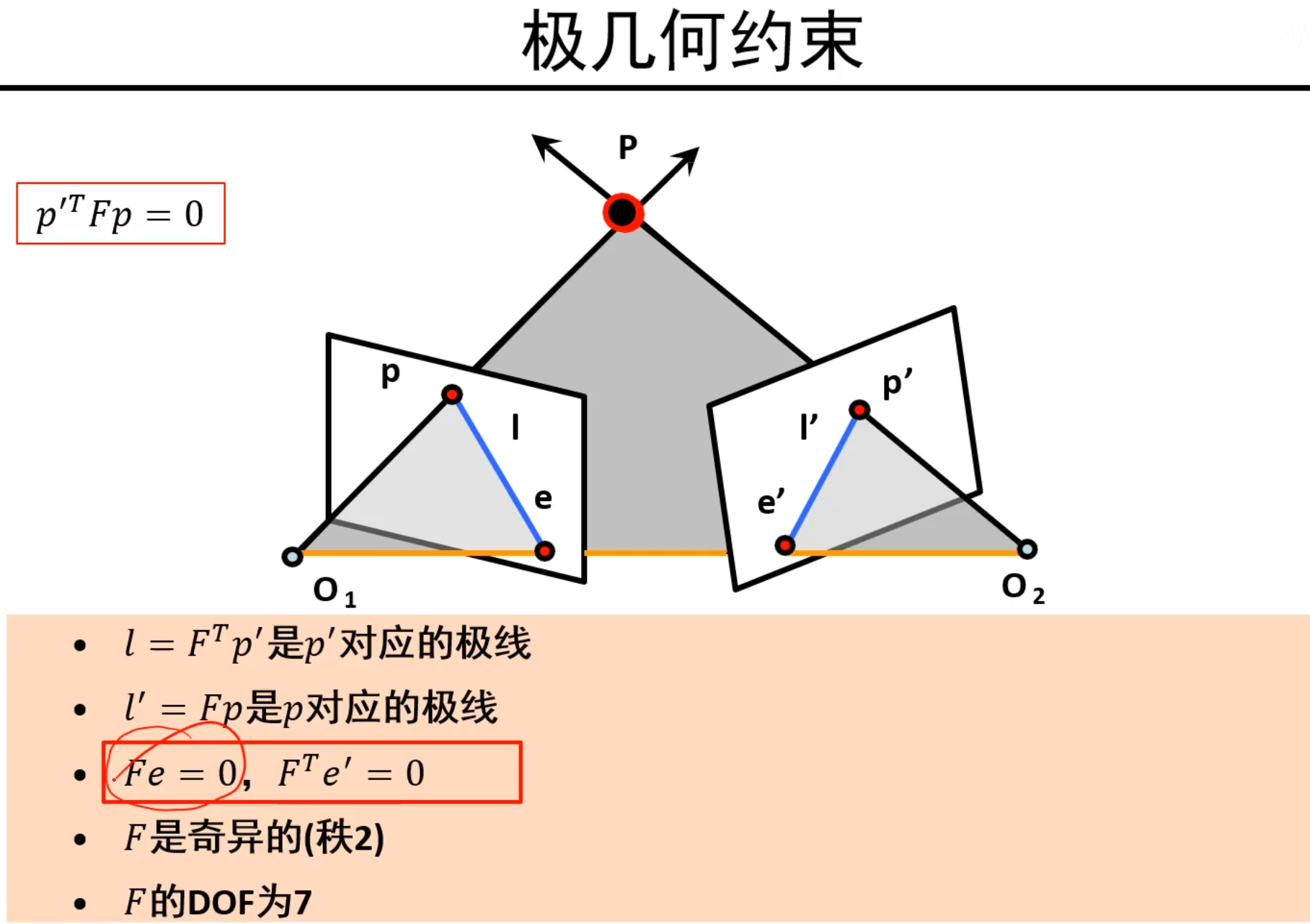

我们发现,b其实就是极点!
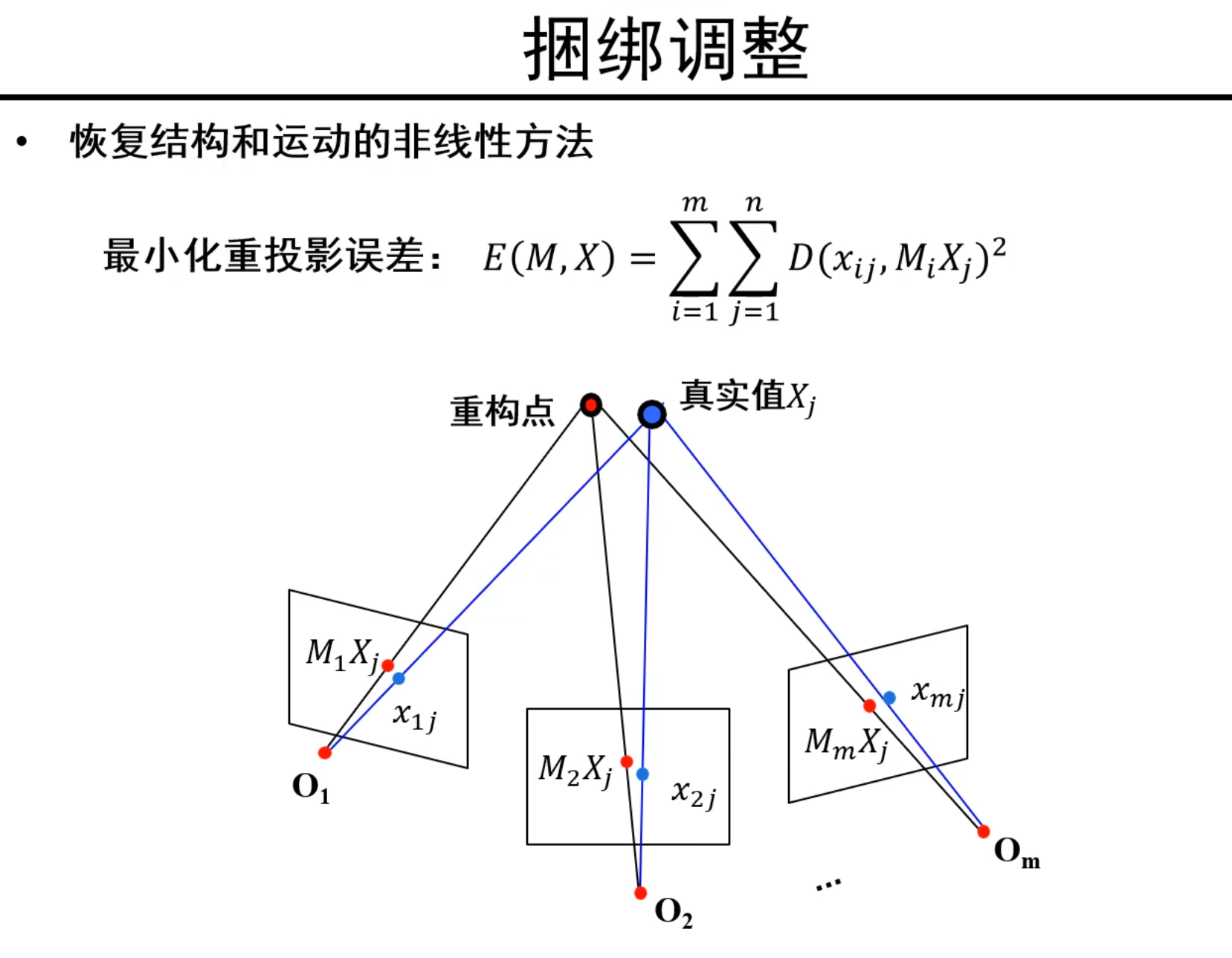
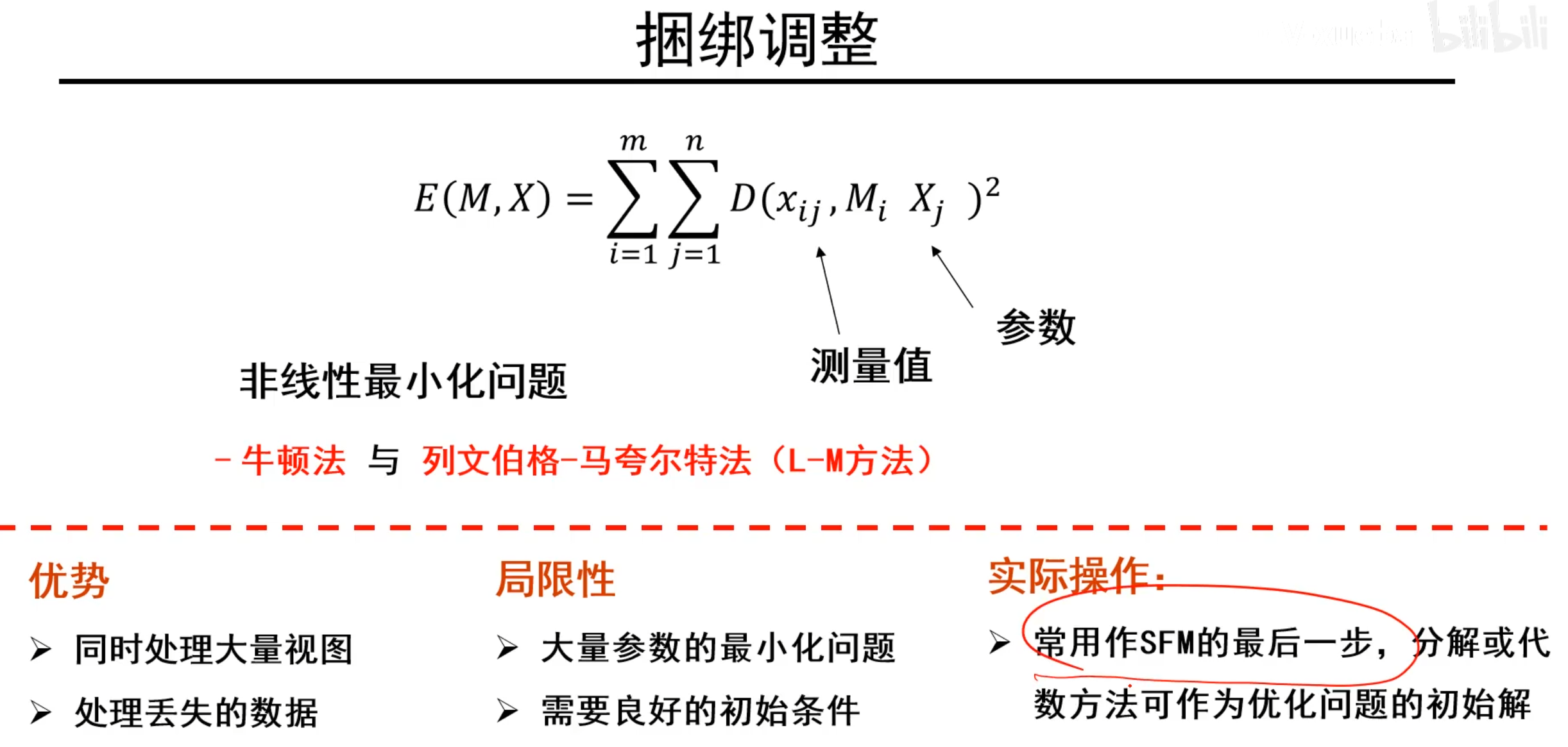
捆绑调整(BA)
代数法和因式分解法的问题

捆绑调整的思路